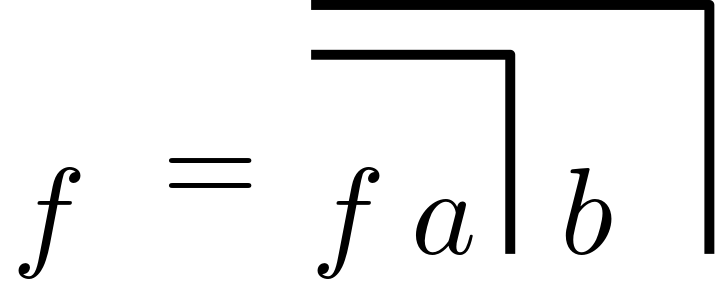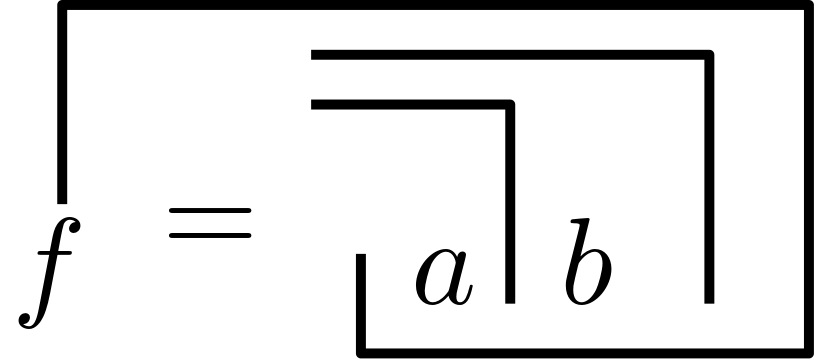Diverging from my area of expertise is always a risky endeavor, but since this is a blog and not a scientific journal, I’m giving myself the liberty to explore and have fun with different ideas (even if the topic is depressing).
Often writing helps in transforming the mess into a structured and coherent concept.
The process of rethinking and reflecting can be invaluable.
It helps to make ones thought anschlussfähig which literally means to be capable for connections and in this context means enabling the continuation of communication.
In this piece, I aim to explore various aspects by linking the movie The Matrix, Plato’s Allegory of the Cave, myths, and conspiracy theories.
Additionally, delve into the understandable yet problematic skepticism surrounding second-order observation.
I will relate this skepticism to the notions of complexity and hyperreality, and discuss why we rely on second-order observation to address the climate crisis.
Some parts of this text will escape a clear interpretation, especially when I offer my interpretation of Baudrillard’s writings.
Some parts might even be contradictory.
But this is the point: enduring or even enjoying ambiguity!
Overall, I hope to give good reasons for the emergence of conspiracy theories and our state of inaction in the face of disaster; reasons that do not rely on a good and evil dichotomy of individuals.
I will argue that our perception of reality makes effective communication between each other improbable and that complex systems follow their own stabalizing dynamic.
In the end, conspiracy theorist will appear as anti-authoritarian rebels that fight against the power of knowledge using the same source of authority, that is, knowledge.
Before we start, let us agree on a definition of conspiracy theories:
By conspiracy theory, I mean an explanation of historical, ongoing, or future events that cites as a main causal factor a group of powerful persons, the conspirators, acting in secret for their own benefit against the common good. – Joseph E. Uscinski
Mythologies, Science and Conspiracy Theories
The phenomena of conspiracy theories hunts and intrigues me since the terror attacks of 9/11 happened back when I was a child.
I remember watching the Zeitgeist series, which linked various conspiracy theories involving religion, the September 11 attacks and the financial sector.
During that time, even German TV occasionally presented documentaries that portrayed certain events in a conspiratorial light.
The shock and uncertainty that the Western world experienced after these events, combined with a sense of lack of control, created a fertile ground for such theories.
These ‘documentaries’ were not only entertaining, but they also sparked my interest in geopolitics, the history of religion, history in general, and even philosophy.
They managed to make historical events captivating, and I often wished that my history classes were similarly engaging.
Fortunately, I never embraced the logic presented in these films; for me, they remained within the realm of entertainment but I could see how easy it is to fall for them on an emotional level.
Interestingly, years later, when a real plot unfolded to deceive the public (and other nations) into supporting the war against Iraq, there was no corresponding emergence of conspiracy theories like those seen previously.
During the pandemic, I observed a repetition of history in the form of similar documentaries emerging, and I became interested in how they were designed and how they relate to the conspiratorial ‘documentaries’ I encountered in my childhood. Indeed, they bore striking similarities.
Apart from the obvious parallels, such as misrepresentation and drawing connections between completely unrelated events, there were also more bizarre links.
For instance, these documentaries often incorporate some form of spiritual concept, promising a return to or discovery of a ‘true self’, an ‘inner peace’ or a ‘forgotten innocence’.
For example, the Zeitgeist series uses a speech from the Indian philosopher Jiddu Krishnamurti (1895 – 1986) but only as an emotional device:
We will see how very important it is to bring about in the human mind the radical revolution.
The crisis is a crisis in consciousness, a crisis that cannot anymore accept the old norms, the old patterns, the ancient traditions.
And considering what the world is now with all the misery, conflict, destructive brutality, aggresion, and so on, man is still as he was, is still brutal, violent, aggressive, competitive and has built a society along these lines. – Jiddu Krishnamurti
In my interpretation, this reflects a lost connection to the wholeness of the universe.
At the extreme end, I experience sometimes two contradictory moods.
First, there is this feeling of alienation in an absurd world, which Albert Camus described best in his book The Stranger.
For me, the absurdity of the world reveals itself when I am out in the city, observing people rushing through their lives, participating in the acceleration towards a promised utopia that no longer exists, not even in their imaginations.
It is also connected to the realization that I was thrown into this world, culture, mess; this contradiction; this meaningless rat race.
The second mood arises from a profound connection with the world.
It feels as if we are the world, as if there is no separation between myself and my environment, between myself and the universe.
Yet, at the same time, I sense a process that is not only mysterious but overwhelmingly greater than I can ever comprehend; a force beyond my intellect.
Such feelings arise, for example, in nature.
When we stand atop a mountain, not thinking but simply being present in the world, or even feeling as if we are the world.
Such a feeling can also arise when we are completely immersed in an activity, like a drummer who dissolves entirely into the act of drumming.
This state of existence requires a quiet mind and a cessation of thought.
Consequently, it was no surprise to me that at the protests against COVID-19 restrictions and at QAnon gatherings, there was a peculiar blend of people, including everyone from far right-wingers to faith healers.
Of course, one has to be careful with such categorization since such protests are often captured by extreme parties.
Anyways, this mix reflects the broad, albeit unusual, appeal of such conspiratorial narratives and the desire for an effective (post-truth) narrator, e.g. Donald Trump, who provides a myth that carries emotional weight rather than the difficulty and uncertainty of a complex world—a myth one can live by.
However, ignorance is too simple of an explanation.
The MAGA cult is not disingaged in communication or the production of knowledge.
Instead they (ab)use communication to construct quite imaginative but also inconsistant alternative facts effectively.
On the basis of knowledge, it is easy to make fun of people believing in mythologies.
Scienficially speaking, myths are either inconsistent or unfalsifiable.
However, socially they can be very useful and powerful.
They explain experience and reduce complexity.
A myth is ment to answer questions and offer solutions to quell the anxieties of the present through stories.
They can serve a useful purpose, particularly in politics.
They create visions, unities and identities among groups such that they can work together towards a meaningful goal—a mission greater than oneself.
Here, a shadow of spirituality plays an important role, be it in the form of the Light of God, Siegfried the Dragonslayer, Achilleus the Greatest of All the Greek Warriors or Donald Trump the Warrior King.
Later I will argue that we should keep the source for spirituality, that is, imagination, ambiguity, and contradictions alive and that science can be abused for a Crusade Against Ambiguity.
In my view, spirituality and science can harmonize with quite well.
Religion, as a subset of spirituality, should be criticised especially if it becomes dogmatic, that is, if it starts a crusade against ambiguity.
But it is a narrow perspective to scientifically dispute the existence of a divine entity, just as it is misguided to interpret religious scriptures in a strictly literal sense.
Religion needs ambiguity.
Therefore, it is peculiar to witness esteemed intellectuals like Richard Dawkins engage in debates concerning the divine, overlooking the potential for a creator amidst the universe’s intricate complexity.
We have a working theory, which we know is true, which explains how you can go from great simplicity to prodigious complexity.
And finally to the sort of complexity which is capable of designing things, of creating things, of working out how to do things.
If you suddenly going to insert a designing machine, a creator, an intelligence at the root of the universe you have just undermined your entire enterprise because your entire enterprise has been to explain how you get to something complicated enough to do design. – Richard Dawkins
When Dawkins discusses evolution, it is easy to agree with him from a scientific perspective.
I want him to defend his theory.
However, he often speaks in absolutes, using the language of dogmatic religion that he himself criticizes.
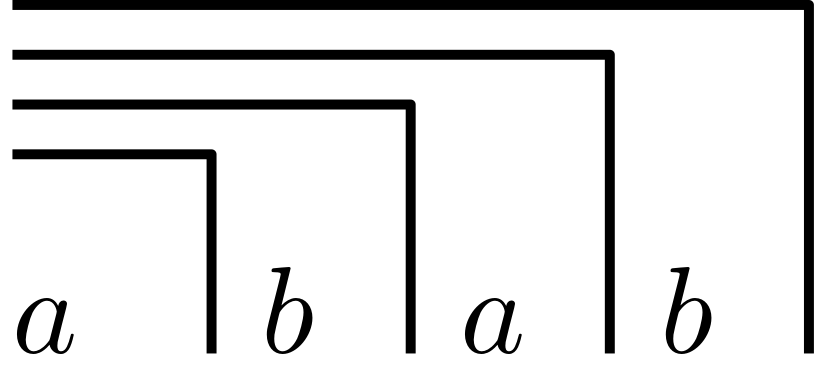
From a systems theory point of view, can resolve this paradox by re-entering itself, that is, by communicating about itself on its own terms—a sort of self-reflection.
Dawkins and similar critics overlook a crucial point: the pursuit of absolute truth is elusive.
Even Dawkins’ assertion that “the theory is true” misrepresents the nature of scientific inquiry, which he is undoubtedly aware of.
Science provides models that explain phenomena until new evidence suggests otherwise.
It mosty works on the basis of falsifiability for demarcation, a concept introduced by Karl Popper (a critic of the inductive theory of science).
The problem of finding a criterion which would enable us to distinguish between the empirical sciences on the one hand, and mathematics and logic as well as ‘metaphysical’ systems on the other, I call the problem of demarcation. – (Popper, 1934)
A statement or system of statements (theory) is falsifiable if it is capable of conflicting with possible, or conceivable observation;
The theory must be able to fail when tested against reality.
Build on rigor and the combination of theory bound by empiricism makes scientific method incredibly useful, and according to philosophers like Markus Gabriel, brings us closer to the Truth.
In contrast, others, such as Richard Rorty, completely reject the notion of absolute Truth and instead emphasize the practical usefulness of the scientific method.
The question of ontology remains unanswered even if most of us operate on the assumption of some sort of naturalism.
It is the principle by which science operates and by which people in well-developed countries often live.
Some define it as “the idea that only natural laws and forces operate in the universe”.
The philosopher Quine described naturalism as “the position that there is no higher tribunal for truth than natural science itself”.
Quine’s more humble and pragmatic definition allows space for profound questions regarding the existence of time, space, causality, and our place within this framework—questions that lie beyond the scope of scientific inquiry.
For him and many others, these are absolute unknowns that can be considered within the realm of spirituality.
These unanswerable questions delve into the essence of being and the universe, inviting a spiritual exploration alongside scientific understanding.
Dawkins seems also to be unaware of the usefulness of ambiguity.
People can hold contradictory beliefs without being irrational or anti-science.
For example, it is unlikely that individuals with a non-dogmatic spiritual outlook adhere to a literal interpretation of the Earth’s creation in seven days or dismiss evolutionary theory but, at the same time, they might believe in a creator.
They can operate in different social systems with different rationals.
This is neither good or bad but a sign of diversity.
I mean how many mathematicians still believe that math has something to do with a divine entity or realm?
Such contradictions only become problematic if systems interfere in the other’s operations, e.g., if religion operates in science or science in religion.
But why can spirituality lead to the descent into the rabbit hole of conspiracy theories?
First of all, there is a strong relation between philosophy, religion, and spirituality, e.g., between Platonism and Christianity.
Monolithic religions offer a rather rigorous explanation of why things are as they are, based on the presumption of a creator.
Especially, non-believers sometimes misunderstand that religious people dislike logic when, in fact, it was Thomas Aquinas who attempted to synthesize Aristotelian philosophy (and logic) with the principles of Christianity.
He produced a vast body of precise, detailed, and systematic philosophical writings, in which he integrated Aristotle’s encyclopedic work and medieval Christian theology into a seamless whole.
The dark side of this was that any contradiction by future scientists would necessarily have to be seen as heresy.
Philosopher Bertrand Russell pointed out that Aquinas started by already knowing the truth in the form of the Catholic faith.
Aquinas used logic to strengthen his belief system and not to question it.
Note that postmodern thinkers argue that philosophers, who practiced metaphysics, did basically the same but in a more clever way.
Famous is Nietzsche’s suspicion of Kant’s categorical imperative, which is, after all, categorical.
Kant, however, pointed to the source of the problem which is not logic or rational thinking but a lack of empirical evidence; a lack of outwardness; of asking nature.
From this perspective, one might say that conspiracists are in the business of doing metaphyics poorly.
It is certainly the case that there are similarities in doing metaphysics and constructing a grand conspiratorial theory (or myth) that attempts to explain everything.
And like Aquinas, theorists of a conspiracy try to establish a kind of system, synthesizing the world into one big theory.
But there are also differences.
Metaphysicians (as well as many religious texts) at least try to be consistent, while conspiracy theorists are liberated from such limitations.
They openly replace rationality with mythology.
By constructing and emphasizing mythological symbols, conspiracy theories provide a shortcut into our soul, psyche, mind, or the unconscious.
They can switch seamlessly from one theory to another.
Myths can be very dangerous.
They misconstrue associations, destroy nuances and advance subconscious theses without the necessary burden of evidence.
Instead of delivering arguments, they short-circuit the entire argumentative process.
Myths do not make logical claims but significations (Barthes, 1973).
For example, calling someone a snake is not a logical conclusion but signifies deceptive behaviour.
Real snakes, of course, are not significantly more or less deceptive than any other animal.
But mythological snakes often are and calling someone a snake can be a powerful gesture in our culture.
Poetry feeds and waters the passions instead of drying them up; she lets them rule, although they ought to be controlled, if mankind are ever to increase in happiness and virtue. – Socrates
If Trump speaks of America or our radical right-wingers speak of Germany, they do not mean literal countries.
They signify a mythological symbol.
An effective myth is a self-contained world of signs were everything has a marked position, making it very hard to signify otherwise with a believer.
To critique their definition as being racist, irrational, exclusive, inhumane, or disastrous only demontrates to them that you are of ‘the them’ (das Man); that you are jealous that they won.
Any contrary narrative is spun by false prophets which conspire against the ‘chosen ones’.
Taking the Wrong Pill
The Matrix is one of my all-time favorite movies, which increased my interest in computer science and philosophy.
As a child, I fantasized about being The One, akin to the hacker Neo, who could hack the matrix.
Interestingly, the movie is inspired by French philosopher and theorist of postmodern media and culture, Jean Baudrillard (1929 – 2007), especially by his book Simulacra and Simulation (Baudrillard, 1983).
The book even makes an appearance (as an empty prop) at the beginning of the film when Neo gives a disc to his clients.
The actors were even reportedly required to read it.
Baudrillard—the prophet of post-truth—focused on analyzing what can be termed postmodern media, although postmodernity is challenging to define.
Thinkers in the field of postmodern theory frequently hold different opinions but there is one core agreement: there are no all encompassing meta-narratives.
For some, such as Niklas Luhmann (1927–1998), the concept of postmodernity itself is contentious, with Luhmann believing it never truly existed (Luhmann, 2000).
But back to Baudrillard.
He was an interesting figure but not taken very seriously by the academic community.
His writing style is polemical and his worldview extremely cynical.
Despite this, his texts are intriguing and thought-provoking, capturing a sentiment that resonates with many facets of our society today.
In many sense, he was ahead of his time and highly influencial in the media and culture he studied.
What particularly makes The Matrix fascinating in connection with Baudrillard is how the film embodies the type of pop-cultural phenomenon he often discussed in his philosophy.
The movie not only reflects his ideas but might be able to bring them to life in a way that is accessible to a broader audience.
Furthermore, Baudrillard was still alive when the movie hit the theatre.
So, did it succeed in bringing his theory to the big screen?
The Simulacrum is True
When we first meet Neo, his computer is active, processing something, with the screen reflecting on his face.
He listens to music through headphones while lying on his desk, asleep.
This scene introduces the difficulty of distinguishing between a dream and reality or more precisely, the problem of informational overload and sensory input that, according to Baudrillard, leads to passivity.
The abundance of disjointed information and excessive transparency makes it nearly impossible to organize the world and assign meaning to it—faces transform into screens or terminals that passively absorb.
In his early career, Baudrillard aimed to merge (post-)Marxism with (post-)structuralism but eventually abandoned the former.
He applied structuralism in his analysis of The System of Objects (Baudrillard, 1968).
Baudrillard theorized that the significance of commodities stems not primarily from their use or exchange value, but rather from their sign value.
In structuralism, the meaning of elements, such as words, doesn’t derive from what they represent.
For instance, teaching a child the word ‘tree’ isn’t as simple as pointing to one and stating, “Look, this is a tree!”
The child wouldn’t know if ‘tree’ refers to that specific tree, its leaves, or a category of trees.
Understanding the word ‘tree’ requires knowledge of many other words and examining their relationships to ‘tree’—their difference.
Baudrillard argues that in a postmodern society, any cultural idea, image, sign, or symbol is apt to be pulled out of its social context and used (or abused) for advertisement and marketing.
The individual is placed in the position of a consumer.
As these signs are lifted out of the social, they lose all possibility of stable reference.
They may be used for anything, for any purpose.
All that remains is a yawning abyss of meaninglessness—a placeless surface that is incapable of holding personal identity, self, or society.
Baudrillard believed that in a postmodern society, the meaning and value of an object are primarily defined by its relationship to other objects.
Apple products serve as a pertinent example.
They appear overpriced when considering solely their use value.
However, their value arises from what they signify in relation to other objects which leads to the demishing of symbolic values.
For example, a pen given to you for your graduation, has probably a high symbolic value to you.
Symbolic values are assigned by a subject in relation to another subject.
Sign value, on the other hand, is the object’s value within a system of objects signifying, for example, social status.
Baudrillard, known for his cynical views, also believed that objects essentially have triumphed over subjects.
He posited that just as money has become a universal medium that renders everything comparable and thus exchangeable, the code has made every sign integratable thus also exchangeable.
It is not that subjects or objects stand no longer for something ‘real’ but that the imagined referent, that does not exist, disappeared.
For example, in the Renaissance people or objects appear to stand for an imagined referent, for instance, royalty, nobility, holiness, etc.
A sign like Iron Man, stands for nothing other than itself in a network of other meaningless signs, i.e. the Marvel universe.
It can be repackaged into a toy or a specific McDonalds meal because it has no sacred connection to the world.
According to Baudrillard, instead of disimulating something, now signs dissimulate that there is nothing.
The transition from signs which dissimulate something to signs which dissimulate that there is nothing, marks the decisive turning point.
The first implies a theology of truth and secrecy (to which the notion of ideology still belongs).
The second inaugurates an age of simulacra and simulation, in which there is no longer any God to recognize his own, nor any last judgment to separate truth from false, the real from its artificial resurrection, since everything is already dead and risen in advance. – Jean Baudrillard
This leads to a kind of dissolution of the ‘real’ meaning behind objects.
Accroding to Baudrillard, in the postmodern world, simulacra (e.g. images) have replaced the reality they once represented.
In other words, our current reality is dominated by these simulacra—representations, images, and signs—that no longer have any connection to any real/imagined object or event they might have originally represented.
Importantly, the simulacrum is not just covering up the truth or reality; it’s not a mask over something real!
In fact, it is quite the opposite.
What we perceive as truth or reality is actually just a construct (the simulacrum) that conceals the fact that there is no underlying, original reality; we enter simulation.
In other words, what we consider ‘real’ is just a construct of our perceptions and societal agreement.
In our current postmodern state, the simulacrum has become the truth for us, because there is no other reality against which to measure it.
The simulacrum is never what hides the truth—it is the truth that hides the fact that there is none.
The simularcum is true. – Jean Baudrillard
Following Baudrillard’s perspective, experiences such as a teenager’s first kiss are no longer real in a sense that they express ‘true love’;
instead, they are mere simulations of a Hollywood love story because these stories are the truth!
Imaginations are not destroyed by hiding the truth but by showing it overtly naked, like pornography rips us of the imaginative allure of sexuality and intimacy.
Life imitates advertisement.
This does not mean that there is no more love.
However, there is nothing behind the ‘Hollywood love story’—it is true as it is.
We are compelled to reproduce these images and to participate, even if we know or suspect that it is all a simulation.
Critically, the problem (if it is in fact one) is not a virtualized reality that hides the truth, but that the truth is simulation.
People are fake but they are turthfully fake because being fake is the truth.
[…] pretending […] leaves the principle of reality intact: the difference is always clear, it is simply masked, whereas simulation threatens the difference between the ‘true’ and the ‘false’, the ‘real’ and the ‘imaginary’. – Jean Baudrillard
When more and more simulacra transform into simulation we enter the matrix.
Pictures of ourselves no longer represent us, or us pretending to be someone else, but they are a simulation of some specific and often stereotypical fantasy that has no reference to something real other than different parts of the code.
That is the depressing and cynical viewpoint of Baudrillard.
Plato’s Allegory of the Cave
I love The Matrix but I have to assess that it did not succeed in capturing Baudrillard’s main themes.
The main problem is a clear line between simulation and reality; between the matrix and Zion.
The matrix clearly is not the truth but hides it.
Rather than exploring the new problem of simulation, the movie falls back on the Allegory of the Cave presented in Plato’s Republic.
Instead of investigating further questions, it postulates a true world behind the simulation by re-introducing religion.
Thus The Matrix brings us back where it all started but, according to Baudrillard, this is no longer possible.
In Baudrillard’s framework, the movie is itself the truth that hides the fact that there is none and therefore distracts the audience from acknowledging hyperreality.
The Allegory of the Cave is a metaphor for exploring the nature of knowledge and reality.
Plato imagined a group of people who lived their entire live chained inside a dark cave.
The only thing they can see are the shadows projected on the wall of the cave by objects passing in front of a fire behind them.
These shadows are the only reality they know.
The cave dwellers believe the shadows to be the real objects, not knowing that these are mere reflections.
Their knowledge and understanding of the world are based solely on this limited perspective.
One day, a prisoner breaks free.
He struggles to adjust to the light outside the cave, but eventually, he sees and understands the true nature of reality.
He realizes that the sun illuminates the world and that what he saw in the cave were just shadows of real objects.
The freed prisoner returns to the cave to enlighten the others.
However, his eyes have adjusted to the sunlight, so the cave is now blindingly dark to him.
The other prisoners, unable to understand his experiences and seeing his blindness in the dark, refuse to believe him.
They cling to their old beliefs about the shadows being the real objects.
In Plato’s metaphysics, the form (true essence of things) are more real than their physical representations.
The shadows represent the physical world, while the objects outside the cave symbolize the forms.
Plato also emphasizes that education is not just a matter of transferring information, but a transformative experience that leads to understanding, or to the seeing of a different world that opens up.
Of course, it is the philosopher that seeks the truth (outside the cave) and then attempts to bring this knowledge back to the people (inside the cave).
We can draw a neat parallel between Plato’s Allegory of the Cave and the film The Matrix by replacing the cave with the matrix and the philosopher with the character Morpheus.
In this parallel, Morpheus takes on the role of guiding Neo (and others) out of the matrix—similar to leading prisoners out of the cave.
Neo learns to understand and manipulate the matrix on his terms, which parallels the ability to manipulate the shadows on the cave walls.
In The Matrix, Neo is confronted with a crucial binary decision, symbolized by the choice between a red and a blue pill.
As revealed in the sequels, this choice is, in itself, a part of a predetermined simulation—a much more Baudrillardian take.
Morpheus presents Neo with this decision and advises him to trust his instinct that something is fundamentally wrong with the world.
This guidance emphasizes the importance of an emotional rather than a logical conclusion, steering Neo to follow his feelings in making this pivotal choice.
Once Neo makes his choice, the distinction between the matrix and reality is clear to him; it is a clear binary: reality and simulation.
True love is still possible outside and even inside the matrix, even if it is predetermined.
According to Baudrillard reality is a simulation echoing Kant, who does not grant us the access to the thing-in-itself, and of course Nietzsche, who tells us that there are only constructed values.
Simualation is nothing bad or something to fear.
It was always already there but the simulacrum (e.g. cave paintings, images) changed towards its own gravity; towards its own perfection.
What Baudrillard feared is a world akin to the movie Minority Report.
A world without reversability where everything is already decided in advance; a world without ambiguity.
In a sense, Baudrillard feared the modern project that started with Plato by looking for some absolut truth or perfect idea.
The perfect simulation gets rid of illusions and imaginations; it is too real; it is hyperreal;
Therefore, Baudrillard did not fear the loss of reality but an exzess of it which would lead to the destruction of illusions and imaginations like the ‘technical perfection of sex’, i.e. pornography, leads to the removal of sexuality and intimacy.
Reality and simulation aren’t opposed to one another.
There are two sides of the same coin. – (Baudrillard, 2008)
With this in mind, if we reexamine The Matrix it becomes clear that Baudrillard would describe it to be a pretty good simulation of the matrix.
In a sense, the sign of simulation is re-integrated into the simulation itself.
This re-integration highlights the film’s exploration of reality, perception, and the nature of choice, themes that resonate with Plato’s allegory but not with Simulacra and Simulation.
Thus Baudrillard concluded:
The radical illusion of the world is a problem faced by all great cultures, which they have solved through art and symbolization.
What we have invented, in order to support this suffering, is a simulated real, which henceforth supplants the real and is its final solution, a virtual universe from which everything dangerous and negative has ben expelled.
And The Matrix is undeniably part of that.
Everything belonging to the order of dream, utopia and phantasm is given expression, ‘realized’.
We are in the uncut transparency.
The Matrix is surely the kind of film about the matrix that the matrix would have been albe to produce. – Jean Baudrillard
A Hunger for Certainty and Definitude
Now, what has this to do with conspiracy theories?
Well, other than Baudrillard’s theory of a reality that is simulation, I claim that the cave allegory offers a theoretical justification for doubting established institutions, which are likened to ‘the matrix’.
One might discover that parts of reality, e.g. institutions, norms, moral judgements, ideologies, is constructed and that there has to be something real behind it.
This suspicion of a matrix is not unfounded, however, believing in some absolut point of view behind it, opens the door to confusion.
We are in a cave but going outside might only lead to another cave.
Importantly, this does not mean that any cave is as useful or functional!
Although not all interpretations of a text are equally meaningful, a good text offers numerous interesting and valuable interpretations and the same seems to be true of our lifeworld.
Doubting parts of reality—a known or presented world—is the starting point of any conspiracy theory.
The perspective is compelling because it feeds the allure of knowing a secret, akin to Neo’s experience in the matrix.
Such knowledge is seen as something that sets an individual apart from ‘the herd’, giving them a sense of being special or enlightened.
It is similar to New Age beliefs in some sort of special knowledge about the universe presented in movies like The Secret.
Belief in conspiracy theories appears to be driven by motives that can be characterized as epistemic (understanding one’s environment), existential (being safe and in control of one’s environment), and social (maintaining a positive image of the self and the social group) (Douglas et al., 2017).
One important facet of conspiracy theories that often goes without much notice is that they are notions about power: who has it and how are they using it?
Conspiracy theories accuse an implicitly powerful group of conspiring.
Usually that group is already powerful—even if that power is a fantasy—i.e., the president, a legislative body, industries or corporations, foreign countries, multinational groups, etc.
Powerless groups are rarely accused of conspiring (Uscinski, 2018).
This also reflects the plot of The Matrix where agents of the matrix are much more powerful than ‘enlightened’ humans.
Studies show that some people are more prone to believing in conspiracy theories than others.
Some people will believe in any conspiracy theory even on light evidence while others, at the opposite end of the spectrum, are naive and will deny the existence of conspiracies even on accumulating evidence (Uscinski, 2018).
According to Jan-Willem Prooijen, conspiracy theories orginate through the same cognitive process that produce other types of belief (e.g. spirituality), they reflect a desire to protect one’s own group against a potentially hostile outgroup, and they are often grounded in strong ideologies.
They are a natural defensive reaction to feelings of uncertainty and fear (Prooijen, 2018).
Interestingly, in studies, individuals who perceive patterns in abstract paintings, random dots, or coin tosses were more inclined to believe in conspiracy theories, paranormal phenomena, and hold religious beliefs.
Belief in conspiracies also tends to rise during natural disasters when people feel a lack of control.
Due to their tendency to seek patterns, conspiracy theorists tend to categorize everything neatly into a framework of good versus evil.
Even though the world that is constructed is miserable, it is without uncertainty.
We are risk calculating creatures, always on the watch for new dangerous patterns.
This is evolutionary advantageous.
Conspiracy is a stubborn creed because humans are pattern-seeking animals.
Show us a sky full of stars, and we will arrange them into animals and giant spoons.
Show us a world full of random misery, and we will use the same trick to connect the dots into secret conspiracies. – Jonathan Kay (Kay, 2011).
Perceiving patterns is the opposite of perceiving randomness, and randomness cannot be the basis for making sense.
Of course, quite often, events occur randomly, without any discernible purpose or meaning.
Sometimes, foolish mistakes simply happen unintentionally.
Research indicates that education reduces the likelihood of believing in conspiracy theories (with exceptions).
This may initially appear counterintuitive because education encourages skepticism toward received wisdom.
Shouldn’t skepticism lead one to think that there might be something hidden behind the scenes?
Well, skepticism is only one aspect of the equation. Education teaches individuals to scrutinize the evidence and seek primary sources, or more precisely, to consider all available evidence.
Under such scrutiny conspiracy theories fall apart.
Moreover, having a greater understanding tends to foster humility since individuals become increasingly aware of the vast expanse of knowledge that remains beyond their grasp.
Scrutiny is built into our institutions.
In the context of academic publishing, one must demonstrate a comprehensive understanding of the relevant literature and show how experiments can be reproduced to validate the published findings.
A peer review process by experts in the field checks for the soundness of the work and identifies possible errors.
While this system is not flawless, makes mistakes, overemphasis the number instead of the value of publications, can be biased, and often favours the middle to upper class, it remains open to critique and has propelled us a long way.
Science is a discourse.
Theories are never absolute true but are seen as true as long as there is no evidence or proof that gives rise to different conclusions.
Mistakes have been made and will continue to be made in the future, but the system is self-correcting, self-preserving, and has advanced our knowledge considerably.
Conspiracy theories are also fueled by our cognitive biases.
For instance, the proportionality bias tends to make us believe that a substantial effect must have a significant cause.
Consider a scenario where either a neighbor or the President of the United States dies randomly; which one is more likely to trigger a conspiracy theory?
Studies have revealed that when people are informed about the assassination of a president, they are more inclined to believe in a conspiracy theory if it coincides with the outbreak of a subsequent civil war (Prooijen, 2018).
Tribalism encourages us to protect our own ingroup and establish a clear division between ‘us vs. them’, often framing it as a battle between good and evil.
The intentionality bias leads us to believe that negative consequences of our actions are unintentional, while attributing intentionality to others when they cause harm.
For example, we may view bankers as evil, but perceive our own pension fund as a necessary institution.
Seeing patterns everywhere is the need for control (Shermer, 2022).
The economy is not this crazy patchwork of supply and demand laws, market forces, interest rate changes, tax policies, business cycles, boom-and-bust fluctuations, recessions and upwings, bull and bear markets, and the like.
Instead, it is a conspiracy of a handful of powerful people variously identified as the Illuminati, the Bilderberger group, the Council on Foreign Relations, the Trilateral Commission, the Rockefellers and Rothshields.
[…] Conspiracists believe that the complex and messy world of politics, economics, and culture can all be explained by a single conspiracy and conspiratorial event that downplays chance and attributes everything to this final end of history. – Michael Shermer
(Landau et al., 2015) show that people compensate for perceived loss of control by trying to restore control themselves by
bolstering personal agency, affiliating with external systems perceived to be acting on the self’s behalf, and affirming clear contingencies between actions and outcomes [… and] seeking out and preferring simple, clear, and consistent interpretations of the social and physical environments.
Narcissism, characterized by a belief in one’s superiority and the desire for special treatment, strongly correlates with a tendency to believe in conspiracy theories.
Narcissists also exhibit heightened sensitivity to perceived threats (Cichocka et al., 2022).
Within the realm of narcissism, grandiose narcissists seek admiration by bolstering their egos through a sense of uniqueness, charm, and grandiose fantasies.
It’s worth noting that narcissists often display naivety and are less likely to engage in cognitive reflection.
Surprisingly, studies have uncovered evidence suggesting that, contrary to expectations, education increases the likelihood of narcissists adopting conspiracy beliefs (Cosgrove & Murphy, 2023).
This underscores the critical role of cognitive reflection as one of the most, if not the most, essential abilities to guard against narcissistic tendencies towards conspiracy beliefs.
[Conspiracy believers] are relatively untrusting, ideologically eccentric, concerned about personal safety, and prone to perceiving agency in action – (Hart & Graether, 2015)
Similar to the experience of emerging from the cave in Plato’s allegory, delving into a conspiracy theory is not merely a transfer of knowledge, but a transformative experience.
It involves a world being shattered and a new one being constructed in its place.
This process signifies a profound shift in perception and understanding, where previously accepted realities are dismantled and replaced with an entirely different framework of belief and interpretation.
Like Morpheus’ emphasis on trusting one’s instincts in The Matrix, conspiracy theories often accurately capture the emotional aspects of a person’s situation.
These theories provide compelling descriptions of emotional states but tend to offer simplistic and reactionary explanations for complex situations.
Additionally, much like the concept of the matrix, they seek an all-encompassing explanation for everything.
Essentially, these theories represent a futile effort to eliminate contingency and the future’s uncertainty.
They attempt to provide a sense of certainty and understanding in a world that (hopefully) is still inherently open, contingent, unpredictable and complex.
This desire for comprehensive explanations reflects a deep-seated human need for order and predictability in an increasingly fatal looking world.
Escaping the Simulation?
The incorporation of expressions like ‘escaping the matrix’ and ‘being red-pilled’ into the vocabulary of conspiracy theory groups as metaphorical language is unsurprising.
These terms, which originated from The Matrix, are used metaphorically to describe the experience of awakening to a hidden or suppressed truth.
This desire might increase with the suspicion that there is none.
Specifically, ‘escaping the matrix’ denotes the recognition and liberation from a controlling system or an illusionary world, while ‘being red-pilled’ represents a moment of profound revelation or enlightenment, often regarding societal structures or purported conspiracies.
These metaphors have gained traction within certain groups as a way to express their beliefs in uncovering what they perceive as hidden truths within society.
They believe to be the philosophers of our age, teaching us how real man behave and how ‘the system’ keeps them weak and small.
Contrary to the common belief that ignorance fuels the acceptance of a matrix-like reality, it is curiosity that often propels this belief.
People are attracted to the notion of discovering hidden truths and understanding the world in ways that differ from the majority’s perspective.
The group forms, in a manner reminiscent of a cult, and establishes easily comprehensible guidelines, resembling the revolutionaries from another pop-cultural and frequently misunderstood film—Fight Club.
The theme of ‘stepping out of the dark’ is central to Plato’s cave allegory, The Matrix, and various conspiracy theories.
Such curiosity ignites a desire to investigate and question conventional narratives, leading some individuals to adopt alternative interpretations of reality.
Interestingly, critical thinking and intelligence do not necessarily prevent one from falling into this rabbit hole.
As described above, these attributes can sometimes drive narcissits deeper into exploring and accepting these alternate realities—the problem is a lack of reflection.
The quest for understanding and the allure of uncovering hidden knowledge can be so compelling that even the most critical and intelligent minds are susceptible to these alternate explanations.
Take the following speech performed by the actor James Caviezel (an actor I once admired for his role in The Thin Red Line) at the end of Sound of Freedom, a conspitorial movie about child trafficking:
While watching this movie, I guess some of you were feeling sad, maybe overwhelmed, or even feel a sense of fear, which is understandable. But living in fear isn’t how we solve this problem. It’s living in hope. It’s believing that we can make a difference because we can.
I want to make one thing clear: this movie you just watched isn’t about me or Tim Ballard.
It’s about those kids. This film was actually made five years ago.
It wasn’t released until now, with every roadblock you can imagine being tossed in our way. [The powerful do not want you to see it, believe me].
And the names you see here, on the screen, took a stand! They made sure that this story could be shown to all of you. Now, all of you have the opportunity to continue telling this story; [the Truth].
We don’t have big studio money to market this movie [(we only have Fox News, one of the biggest network in the country)], but we have you. The baton has now been passed to you. You are the storytellers who can get people to come see this film in theaters. Together, we have a chance to make these two kids and the countless children they represent the most powerful people in the world by telling their story in a way only cinema can.
For a couple of months, while Sound of Freedom is in theaters, these kids can be more powerful than the cartel kingpins, presidents, congressmen, or even tech billionaires. We believe this movie has the power to be a huge step forward toward ending child trafficking, but it will only have that effect if millions of people see it.
We don’t want finances to be the reason someone doesn’t see this movie, so Angel Studios has set up a forward program where you can pay for someone else’s ticket who might not otherwise see it. If you’re able, we invite you to pay it forward by buying a ticket for someone else, or if your budget is tight, share the already available free ticket with as many friends as you can.
Join us and millions of others as we ring Sound of Freedom and hope throughout the world. And just remember this: God’s children are not for sale.
During the speech a QR Code and the text “Give an Share Tickets / ANGLE.COM/freedom” is displayed.
This speech is filled with pathos, it is shamelessly manipulative, moralistic, heroistic and serves a narcissist desire to ‘wake up’, spread the word of Truth or God and become the hero; a soldier of Freedom; an angle of God; a righteous martyred that saves us all.
It is also conspiratorial.
Of course, in the same breath Caviezel tells us to buy tickets to end child trafficking which is not only irrational but flat out unethical and morally dubious.
It is so obviously a scam that it becomes an interesting field of study why people buy into it.
Does the deeply religious actor James Caviezel believe what he is saying? I think he does on some level.
He explained at a promotion event for the movie that billionaires capture children to extract adrenalin out of their blood when they are scared of death, which is a famous QAnon conspiracy theory.
These people that do it; there will be no mercy for them! – James Caviezel
The speech is also kind of Baudrillardian in that sense that even the fight for the Good is just a struggle to buy that god damn ticket; even God’s angles are reduced to passive consumers.
At the same time it is not about the kids but a much more sacred war of Good against Evil—a mystic war in a very angry United States of America!
A country that is at the brink of an inwardly directed outburst.
Everyone in the media is so angry all the time.
This angry speech and movie, that abuses religion, confirms my believe that I should not fear the people who name themselves after the Devil but those who name themselves after a righteous God.
Nietzsche was right about that.
Now, it is a fact that people do engage in conspiracies (and that child trafficking is a big problem).
A brief examination of history reveals numerous instances of conspiracies, some of which have even led to wars between nations.
However, in retrospect, these conspiracies can often be explained without assuming the involvement of thousands of people.
The complexity and impact of these historical events do not necessarily require large-scale collusion; often, they can be understood through the actions and decisions of a relatively small number of individuals or groups and through a systemic rationality.
This understanding helps differentiate between plausible historical conspiracies and the more elaborate, less credible theories that claim widespread secret collaboration.
If it exists, the matrix is not a planned construction of anybody but a Baudrillardian process beyond anyones control.
In addition, it’s important to recognize that the world is inherently unjust.
Justice is a human concept, one that evolves over time as we make what we call progress.
However, in the realm of nature, there is no concept of justice at least none I am aware of;
nature operates outside of morality.
Absolute justice remains elusive and if we seek an explanation for the world’s injustice, conspiracy theories provide a sense of comfort.
It appears to me that the belief in having escaped the matrix or emerged from the cave is a strong indication of someone having entrenched themselves deeply in their own perspective—failing to see that their perspective also relies on some sort of second-order observation; a following of the herd, or in Baudrillard’s viewpoint, the false assumption that there is something true behind the simulation.
This belief offers comfort by addressing various uncertainties and the realization of one’s own ignorance.
No one desires to be ignorant and no one wants to rely on some sort of authority, yet in many ways, we all are.
In our complex world, this is an unavoidable reality.
Conspiracy theories provide a sense of understanding and control in a world where complete knowledge is unattainable, helping individuals cope with the inherent limitations of human understanding.
Therefore, I believe that individuals who are particularly uncomfortable with uncertainty, who seek control over their life, and who are actively aware of their lack of control, are more susceptible to falling into these rabbit holes of alternate realities.
Additionally, a certain degree of narcissism may be necessary to believe in the premise that one possesses a superior ability to understand complex matters better than trained experts and to assume that the media consisting of hundred of thousand of journalists is a monolith.
This combination of a need for control, discomfort with uncertainty, and a self-perceived exceptional understanding can lead individuals to embrace alternative explanations that offer a sense of clarity and personal significance in a complex world.
If we contemplate the matrix envisioned by Baudrillard, then attempting to escape it through the immersion in an alternate version of reality, fostered by extensive consumption of social media and digital content, appears absurd.
Perhaps a more appropriate approach to disengaging from the machinery of simulation and countering the sensation that reality seems increasingly tenuous is to simply disconnect from it all (from time to time).
When advertisements, repetitive media, individuals transformed into brands, and an incessant stream of content seize our attention, the signal overflow—the noise—overshadows a more tangible reality.
In a scenario where there may be no external escape from the simulation, it could be valuable, from time to time, to focus on what is immediately before us: to experience, touch, smell, listen to our bodies, engage with physical sensations, concentrate, savor awareness, and relinquish the illusion of the “real” by re-connecting to a spiritual world.
We are not superheroes; we are composed of the same fundamental elements as everything else.
While it might feel like we inhabit a sort of matrix, it’s essential to acknowledge that this is a choice we make.
From childhood, we develop self-conceptions and fantasies, but this doesn’t negate the existence of the world itself.
Fantasies are constructs, and doubting the existence of the world presupposes a profound level of experience and knowledge of that world—a world where we learn to eat, walk, dance, and understand the nuances of correct and incorrect language usage.
Doubting it requires a distance from it and that might be what social media does: it shrinks the world but increases the distance to it.
We often employ our habits so routinely that we forget we are employing them, and in doing so, we forget that the world—our home—is still there.
The central question here is what is more reasonable to doubt: the world we intimately grew up in or our doubts about doubting it?
Our Dependence on Second-order Observation
Thinking critically and maintaining a sense of curiosity are attributes that I certainly hope everyone possesses.
It is crucial that institutions, including large media operations, research institutions, and particularly governments, are consistently challenged and kept under close scrutiny.
Conspiracy theories can serve as a force to encourage the prevention of corruption.
I would be quite suspicious if there were no conspiracy theories present!
Simultaneously, these theories have the potential to divert attention from genuine issues.
The public should advocate for accountability and transparency, cultivating a healthy and well-informed society in which decisions and policies undergo scrutiny and improvement through public discourse and critical examination.
However, as the current state of affairs stands, the notion that everyone can participate in the marketplace of ideas and engage in public discourse seems somewhat impractical and utopian.
This dream may appear overly optimistic, excessively humanistic, and excessively individualistic.
Instead, according to Luhmann, there exists an interdependent network of social systems that co-evolve together—not individual souls but interconnected systems.
Similarily we demand the media should try to be as objective as they can be but it is naive to think that they are able to present reality as it is.
Here I agree with Luhmann:
It is impossible to understand the reality of the mass media if you assume it is their job to provide correct information on the world and then assess how they fail, distort reality, and manipulate opinion—as if they could do otherwise. – Niklas Luhmann
Basically, Luhmann observed something very similar to the Manufacturing Consent (Herman & Chomsky, 1988) but explains it slightly differently without the need for a propaganda model.
If one anticipates that the primary purpose of the media is to deliver accurate information or facts, they are likely to encounter inconsistencies that raise significant doubts about the credibility of the mass media apparatus.
The media is inherently self-preserving.
It functions in a manner that constructs and sustains itself.
While it is certainly beneficial for the media to provide accurate information, this is not its foremost objective.
The media provides what is known to be known.
It irritates politics, our economy and the scientific system while bing irritated by all these systems.
The media makes society restless.
The view that the media presents ‘the Truth’ contributes to the proliferation of conspiracy theories, since it portrays the entire system as corrupt.
If the media presents objective facts and these facts are inconsistent, distorted, incomplete and open for interpretation then it is disfunctional or corrupt.
Instead of recognizing the various shortcomings (which serve the internal logic of the system) within the media (of which there are many), one tends to assume a broad conspiracy aimed at deliberately deceiving the public.
This leads to a pervasive distrust, particularly directed towards well-established media outlets.
As a consequence, consumers may turn to ‘alternative’ media sources, even though these alternatives often inadvertently rely on established media institutions for their information.
Reporting, conducting on-site investigations, collecting information, and managing extensive archives are expensive endeavors that only large institutions can effectively undertake.
These institutions are essential if we are to have any hope to share a world that is at least partly commonly known.
The core issue lies in our reliance on what Niklas Luhmann refers to as second-order observation and is consequently a trust issue.
In modern society, directly observing reality is increasingly challenging.
To stay informed about various aspects such as the state of the economy, job market trends, recent fashion styles, developments in one’s favorite sports league, or new scientific inventions and studies, it is impractical to personally verify these facets.
Instead, we depend on the observations made by others and, of course, machines.
This means we have to engage with various forms of reporting and analysis: reading reports about the GDP, considering the opinions of fashion critics, watching sports programs, and reviewing scientific papers.
In science, we write review papers about review papers.
We track how often papers are cited, i.e. how these papers are being observed.
This reliance on second-hand information shapes our understanding of the world, as we depend on external observers to provide us with insights and knowledge about various domains that we cannot directly experience or verify ourselves.
We are frequently depend on multiple layers of second-order observations or various levels of abstraction.
Scientific papers serve as a prime example.
These papers are typically not intended for a general audience but are meant for peers within the specific field of research.
As a result, the average person often finds them inaccessible.
Consequently, we turn to science communicators and mass media to distill and present scientific information.
These intermediaries play a crucial role in interpreting and translating complex scientific data and studies into ‘facts’ that are understandable and relevant to the general public.
This reliance on filtered and simplified interpretations highlights our dependence on external sources to understand and engage with specialized knowledge areas.
At the core of our society is the notion of the individual as a subject capable of making their own decisions and drawing sound conclusions.
However, it’s evident that our understanding of the numerous processes occurring around us is limited.
The complexity of the modern world might only be manageable through functional differentiation and second-order observation.
We are heavily dependent on specialists and experts, and our understanding is largely shaped by observing their observations.
Conspiracy theorists seemingly reject second-order observation, viewing it as a form of manipulation akin to the matrix.
However, this rejection is a perilous illusion.
There is no position outside of second-order observation, no external vantage point from which to objectively assess ‘reality’ as it is, separate from the interpretations and understandings provided by others.
This perspective underscores the intricate and interconnected nature of knowledge and understanding in contemporary society.
Philosophers ranging from Plato, Fichte, and Kierkegaard to Russell, Kant, and Heidegger have provided insights that prompt us to question the application of second-order observation.
These philosophical teachings encourage us to contemplate whether we should exercise independent thinking and challenge the prevailing mainstream narrative.
This concept is epitomized in Heidegger’s notion of avoiding assimilation into das Man (the they), Kierkegaard’s emphasis on distancing oneself from the public, or Fichte’s focus on the ego.
The stories goes like this: There exists an inner truth within us, and we should search within our authentic selves to discover it.
As sovereign individuals in a libertarian society, we should not solely rely on the opinions, or observations, of others.
As Kant famously articulated, we should have the courage to employ our own intellect (Verstand).
I align with Kant with a caveat: we should also have the courage to acknowledge our own ignorance and cultivate the ability to rectify it.
By utilizing second-order observation wisely, we can develop a cultural intelligence more akin to Hegel’s concept of the world spirit than Kant’s emphasis on the individual.
Conviction under Constructivism
Biologists Humberto Maturana, Francisco Varela, Samy Frenk, and Gabriela Uribe made a significant discovery regarding our understanding of color perception.
Rather than focusing solely on the correlation between the physical source of color and the retina’s response, they emphasized another more important correlation: the one between the retina and subjective color perception.
In this context, the external source of color functions as a trigger, not the sole determinant.
This structure of subjective color perception effectively maintains the perception of colors under various objective conditions, even when there are substantial discrepancies between the perceived and ‘emitted’ color, as seen in deception experiments.
Maturana and Varela extended this insight to introduce the concept of autopoesis, integral to the biological theory of cognition (Maturana & Varela, 1987).
In line with their constructivist theory, every individual constructs their own cognition and, by extension, their reality.
In fact, for Maturana cognition is living.
His theory seems not far from Kant’s and to an extend Fichte’s understanding of cognition.
Constructivism does not imply an absence of a single reality or a state of complete subjectivity, but rather, it leads to some noteworthy conclusions:
- An absolute system of values and knowledge cannot exist because personal experience forms an unshakable foundation.
- Convincing someone can only succeed when they develop their own system of conviction.
- Humans, capable of observing their cognitive actions and recognizing the relativity of their seemingly valid knowledge, face the responsibility of choosing and adhering to their own value system.
These conclusions have significant relevance to our current discussion.
Maturana’s framework explains the challenge of debunking conspiracy theories and how individuals can inhabit vastly different realities.
It also underscores our responsibility to acknowledge our inherently constructed perspective on reality and the value system we embrace.
Now, I should mention that there are numerous critics of constructivism, including Markus Gabriel, who advocates for what he refers to as new realism.
In his book Der Sinn des Denkens (English: The Sense of Thinking) (Gabriel, 2018), he writes:
Constructivism is incorrect. New realism asserts that we can perceive reality as it is, without there being precisely one world or reality that encompasses all objects or facts that exist. – Markus Gabriel
I read his book with the expectation of finding a plausible justification for why this should be the case, but I couldn’t find any consistent argument.
Admittedly, this might be unfair as the book is a popular science book and doesn’t aim to provide a rigorous theory.
Nevertheless, Gabriel often labels assertions as obvious without offering a reasonable explanation.
Based on what I’ve encountered and also observed in my own life, I lean toward believing in constructivism.
Certainly, this form of relativism raises several pressing issues.
For instance, how can we justify the actions of individuals whose worldviews may vastly differ from our own?
Additionally, how can international bodies like the United Nations apply pressure on nations that violate human rights if their value systems diverge significantly from a Western dominated notion of values?
Richard Rorty has an intreresting take on that question.
If we want universal acceptance of and respect for human rights, we shouldn’t try to argue about it.
We shouldn’t attempt to work out rational justifications of human rights, or arguments that will convince people that human rights are a good thing.
Instead, according to Rorty, we would achieve better results if we try to influence people’s feelings instead of their minds—philosophy as poetry (Rorty, 2016)!
Rational justifying human rights is an abstract and philosophical way—something that, according to Rorty, isn’t possible anyway.
In a sense, Rorty suggest that, instead of arguing rationally against mythologies, we should imagine, construct and present better ones.
He does not believe in a second enlightenment—in which logic and rationality will triumph over evil.
It is worth noting that similar challenges and questions arise when we consider the concept of free will, which is itself a highly contentious notion, compare for example (Sapolsky, 2023).
In a world with no singular perspective, there are multiple viewpoints coexisting and each has its inherent blind spots.
According to Luhmann, this principle applies to any observing system, whether it’s a psychological system, like the human mind, or a social system.
The diversity of perspectives inherently limits each view, preventing it from fully encompassing all facets of a situation or concept.
Observation is blind to its own conditions.
When I observe a tree I can not (at the same time) observe myself observing the tree.
This inherent limitation in observation highlights the intricate and multifaceted nature of comprehending and interpreting the world around us.
The diversity of perspectives among individuals often complicates accurate communication because each of us essentially speaks a slightly different language.
Communication, in itself, can be seen as improbable.
In addition, language is not something we use to describe reality accurately but a technique we employ to get things done.
Nevertheless, communication remains a crucial element as it plays a central role in stabilizing the chaos and connecting psychic and social systems.
Interestingly, it can be effective even when we don’t fully comprehend each other.
A prime example of this is ChatGPT, which may not understand as humans do but still manages to communicate effectively.
So, can we embrace and navigate this diversity of perspectives?
Can or should we tolerate the uncanny sensation of numerous distinct realities coexisting?
Is it possible for us to, to some extent, accept that others may inhabit a differently constructed world while simultaneously acknowledging the existence of something that persists, even if we cease to believe in it.
After all, our constructions do not follow our beliefs—we can not dream the problem away.
The Reality of the Climate Crisis
The COVID-19 pandemic had a measurable positive effect on pollution levels—which did not last for long.
However, one could argue that it also had a negative impact on trust levels in institutions, especially scientific ones.
This erosion of trust may ultimately hinder efforts to address the climate crisis.
The ongoing debate regarding climate change’s origins and the necessity of curbing CO2 and equivalent gas emissions continues to persist even if the scientific community is clear on the matter—a conviction I have established via second-order observation.
It appears to me that COVID, combined with the rapid and highly polarizing consumption of “news” on social media, has fractured our social discourse.
The culture of dialogue has suffered, forcing individuals to align with one of two extreme sides.
It now seems impossible to critique one party without facing accusations of working for the other.
The language we employ has become more moralizing.
Instead of characterizing people as simply incompetent, misled, misguided, or influenced by flawed incentives within a system, they are often labeled as evil.
This focus on the individual impedes progress in reforming social systems, which are in need of change to provide alternative incentives that prioritize social, ecological, and economic measures for all inhabitants of the planet.
Part of the reality of the climate crisis is that we need trusted institutions that need to be aligned in a way that dealing with the crisis becomes possible.
Emissions are not the only problems on our hand.
Many ecological systems are on the bringe of collapse.
Our agriculture is under threat.
Water shortages are on the horizon.
Increased carbon dioxide absorption by oceans leads to ocean acidification, which can harm marine life, especially coral reefs and shellfish.
Climate change can exacerbate health issues by increasing the spread of diseases, heat-related illnesses, and air quality problems due to wildfires and increased pollen levels.
Changing weather patterns and more frequent extreme events can disrupt agriculture and water supplies, potentially leading to food shortages and conflicts over resources.
As climate impacts worsen, there will be never-seen increased migration and displacement of populations, both within and across borders, as people seek refuge from areas affected by climate-related hazards.
Climate change is very likely to intensify extreme weather events such as hurricanes, droughts, heatwaves, and heavy rainfall.
These events can lead to increased property damage, displacement of populations, and economic losses.
Sea levels are expected to continue rising, posing a threat to coastal communities, infrastructure, and ecosystems.
Flooding and saltwater intrusion into freshwater sources may become more common.
I imagine that, at some point, borders of certain countries will be closed, dividing the world in a real and a hyperreal one.
Considering all the points I discussed, the resistance to transitioning away from fossil fuels is expected, given the various parties involved.
It would be a relief if we were in a simulated reality, where everything could be dismissed as a bad dream.
However, we are faced with the pressing need to convince everyone that climate change is a real problem that demands immediate action.
And that it is worth to sacrifice for the unknown other.
Individuals who have limited information may be persuaded through sound arguments and credible sources.
However, those who actively reject the mainstream narrative may ultimately question the legitimacy of second-order observation.
An example of this dynamic in action was during a BBC News panel where Brian Cox (physics professor and science communicator) clashed with skeptic Malcolm Roberts (politician).
Roberts insisted on empirical evidence and rejected appeals to authority.
All seemed well and logical, but when Cox presented a graph as evidence, Roberts dismissed it, alleging that the data had been corrupted by NASA.
At this juncture, a discussion is no longer possible because there are no external empirical evidence available beyond that produced by scientific institutions.
Undeniable empirical evidence, including temperature records, ice melt data, and rising sea levels, serves as a compelling testament to the tangible effects of climate change.
To promote a more informed perspective, it is advisable to encourage individuals to explore and critically evaluate reputable, peer-reviewed scientific sources, rather than relying on fringe or biased information.
So, let’s delve into a tiny selection of influential contributions from the scientific community that have shaped our understanding of climate change.
Note that this is only a tiny selection from the whole corpus:
As early as 1896, Svante Arrhenius published a groundbreaking paper on the greenhouse effect, demonstrating how rising concentrations of greenhouse gases lead to an increase in global average surface temperatures (Arrhenius, 1896).
Another significant milestone occurred in 1967 when Manabe and Wetherald published the first paper that incorporated the fundamental elements of Earth’s climate into a computer model, exploring the implications of doubling carbon dioxide levels for global temperatures (Manabe & Wetherald, 1967).
Remarkably, the results of their work remain valid today, according to Prof. Forster.
In 1976, Charles D. Keeling and his team documented a pivotal moment by revealing the sharp rise in carbon dioxide levels at the Mauna Loa observatory in Hawaii (Keeling et al., 1976).
This paper highlighted the observable increase in atmospheric CO2 resulting from the combustion of carbon, petroleum, and natural gas.
Fast-forwarding to 2006, Held and Soden advanced the concept known as wet-get-wetter, dry-get-drier precipitation in the context of global warming (Held & Soden, 2006).
This idea, though occasionally misunderstood and misapplied, remains the first and perhaps the only systematic conclusion regarding regional precipitation and global warming based on a robust physical understanding of the atmosphere.
Additionally, the Intergovernmental Panel on Climate Change (IPCC) reports have played an integral role in consolidating and disseminating crucial climate science findings, further enhancing our collective comprehension of climate change.
If one is convinced that there may be some shadiness going on, I encourage the reader to delve into the extensive history of climate change science, for example The Discovery of Global Warming (Weart, 2008).
Additional, one can highlight the overwhelming consensus among climate scientists and scientific organizations that climate change is real and largely caused by human activities, compare (Myers et al., 2021; Lynas et al., 2021; Cook et al., 2016; Cook et al., 2013; Doran & Zimmerman, 2009).
Of course, if we only rely on those papers we have to trust an even higher-order observation!
In addition, one can argue that there is no plausible alternative theory apart from the effects humans caused by polluting the planet.
But if an individual has lost trust in institutions, all these efforts will be fruitless.
Therefore, it is so deeply important that our scientific institutions as well as the media defend and improve their reputation.
Without the trust in the other, I see great danger on the horizon, especially if things become increasingly difficult.
The challenge lies in persuading individuals who harbor skepticism, particularly toward what climate change deniers label as mainstream science.
According to Maturana, convincing someone can only happen when they develop their own system of conviction.
This aspect is especially crucial to consider.
Therefore, engagement must be respectful.
It’s essential to take the worries, fears, and arguments of deniers seriously, even when they appear unreasonable.
However, it is also important to remember that while we encourage others to develop their convictions, we should also acknowledge our own unique and potentially flawed convictions and remain true to them if we are not convinced otherwise.
I think I do it always through stories, never through direct confrontation.
Because if you directly confront somebody who’s thinking polar opposite to you, they don’t really listen.
They are thinking of arguments to refute to. […]
The first thing is to listen to them because maybe they’ve got a point, maybe they’re doing something you never thought about.
But if you still feel that you’re right, then you must have the courage of your conviction. – Jane Goodall
There is another more systemic problem at hand: There is an entire self-producing industry centered around climate denial.
Our society has fostered an army of lobbyists whose primary aim is to actively sabotage progress in addressing climate issues.
In contrast to these ‘knowledgable’ deniers, scientists are required to rigorously justify every aspect of their research repeatedly and tend to be cautious about offering concrete advice.
Conversely, climate deniers merely need to sow seeds of doubt; their strategy revolves around raising questions rather than providing evidence-based answers.
This asymmetry in approach creates a challenging environment for advancing scientific understanding and consensus on climate change.
Rebels of Authority
Apart from ignorance, selfish interests and plain stupidity, I have not yet pointed to the root problem.
I cited papers that suggest that there is a link between pattern matching skills, narcissism and believing in conspiracy theory.
Stupid people elect stupid and corrupt politicians, right?
But that is too easy of an explanation.
Whenever I have to fall back on stupidity or evilness, I get the feeling that I am missing something.
Most of the time peope are not evil or stupid.
Similar to conspiracy theories, such a rational is too simple, too individualistic and also too dangerous.
So what is the systemic reason why people reject actions required to keep the planet sustainable for us all?
Of course, there are many complex reasons but I want to focus on one that fits the meat of this article.
I more or less successfully tried to problematize the search for an absolute objective truth by pointing out that those who believe in stepping out of the cave go probably deeper into it.
And I pointed to Baudrillard’s imagined eradication of imagination leading to a true simulacra that no longer stands for anything but itself—a description of hyperreality that hits me emotionally.
Now, let us imagine that conspiracy theorists rightly point to a problem they might not really understand rationally but feel intuitively.
What might it be?
If we want to describe our modern Western society, I think it’s fair to say that we are a knowledge-based society.
Since Foucault’s historical analysis, we know that knowledge and power are linked.
In our daily life, most of our decisions are informed by some scientifically produced piece of knowledge.
For example, our diet is informed by scientific research that gives us guidance to stay healthy.
How often or for what reason we go to the doctor is informed by science.
In fact, we wittness a whole industry of self-optimization that claims to be scientific.
There are cults trying to establish a ‘science’ of finding a breeding mate.
Or take this article.
My goal and strategy of achieving it is similar: I employ knowledge and second-order observation by citing scientific papers.
In that sense, I fall into the same trap, that is, I try to convince my opponents by displaying superious knowledge.
Since Foucault
In such a society, we tend to search for the perfect algorithm that can make the best decisions for any situation.
In fact, many decisions are already made by algorithms based on the observation of large amounts of data.
Even policies are crafted by utilizing artificial intelligence.
The idea is simple: instead of shouting at each other about the right course of action, let objective reality be the final judge; let ‘the Truth’ decide—let science guide us through the mess.
This is the dream born out of the Enlightenment and it sparked many ideologies that promised to fulfill this utopian harmony.
It is supported by the mechanistic view on the universe suggesting that we can eventually understand all causal relations going back to some final cause we might call God;
In its current interpretation, I call it algocracy (Danaher, 2016), i.e., rule by algorithms.
Interstingly, most conspiracy theorist argue within this framework, that is, they argue not in terms of values but in terms of better knowledge.
At the same time they rebel against the authority of such algorithmic rigor.
Therefore, on the one hand, they believe in a complete understanding of reality or at least a big and very complex chunk of it.
Consequently, they also buy the idea that politics is basically determined by the most powerful authority: the truth.
On the other hand, they rebel against this doctrine by using its own logic.
I think here lies a great danger because the system harms itself by its own operation.
The system enters a process of selfdestruction.
Like Pippi Longstocking, conspiracy theorists create their world or imagine it based on an alternative system of turth.
In the case of Pippi Longstocking, we find this antiauthoritarian attitude charming, creative, and imaginative, but in the case of conspiracy theorists, many find it dangerous, idiotic, and ignorant—an inconsistency worth investigating.
According to the sociologist Alexander Bogner an overdose of antiauthoritarian attitude becomes problematic if we no longer agree on any foundation making any conflict impossible since there is nothing to argue about.
One of such foundation is the belief in an objective truth.
He pragmatically argues that:
For libaral democracies, the idea of objective truth is a necessary fiction. – (Bogner, 2021)
This statement seems reasonable but I will problematize it later.
Bogner points out that a liberal democratic society requires conflicts grounded in dissent.
However, dissent is only possible if there is at least a shared foundation and also an alternative to think about.
Overall, I think Bogner’s essay aligns closely with the constructivists viewpoint shared by e.g. Luhmann even if he criticizes the theory for attacking the idea of an objective truth.
For example, he argues in a Luhmannian manner about the root problem of conspiracy theories, or what many call the post-truth society, pointing out the crossing of boundaries between two interdependent but operationally closed systems:
science and politics.
Due to the functional differentiation of modern societies, politics communicates about values and science communicates about facts.
Bogner argues that today this distinction is blurred leading to dysfunctional systems.
Nowadays, politics communicates about facts but is still guided by values.
This makes productive dissent difficult because different value systems no longer compete within the boundary of values but hide behind the battle for better knowledge.
Values are no longer up for debate.
Instead we argue for superior facts.
In this context, fake news take part in a new language game that is born out from the lack of alternatives.
Fake news do not attack values but knowledge itself.
This could also be observed during the coronavirus crisis:
Due to the high pressure of scientification, the will for fundamental opposition in some places was discharged through the spread of ‘alternative facts’.
[…] It was directed against a (supposedly) authoritative instance that claimed to determine what is real, rational, and politically necessary through superior rationality.
From the perspective of this protest, political emancipation could only be an emancipation from the facts.
Alternative facts are evidently in vogue when politics (due to its alignment with science) appears to be without alternatives. – (Bogner, 2021)
Bogner correclty points out that scientific knowledge can be dangerous for politics because it dismantles or defuses the discourse.
It is also attractive if one wants to surrender responsibility because in science it is far easier to agree on statements since it follows a strict true-false distinction.
In this sense, science is authoritarian.
Take a simple example such as health.
Before talking about it, we already share certain values.
For example, most people probably assume that a long healthy life is preferable over a short or unhealthy life.
This seems reaonable.
However, even this seemingly simple assumption can not be proven.
It is a value and values are mutually constructed.
I can, for example, easily argue that it is better to live to the fullest even if this means that my life expectancy drops.
In politics we argue about values and try to find some common ground.
This requires some degree of cohesion.
It goes against our more and more individualistc togetherness.
Bogner points out that people are considerably constrained in their expression of dissent if scientific truth is translated into a politic that knows no alternative.
His statement resonates with the relation between the belief in conspiracy theory and narcism.
He writes:
The struggle against science and experts can thus be understood as a struggle against determinations that were not chosen by oneself.
For such determinations must appear as an impudent imposition to the individualized, modern person, who is increasingly called upon today as a self-responsible shaper of their destiny, as a self-entrepreneur or ‘Me Inc’.
Therefore, the struggle against facts is, not least, a struggle for autonomy.
From this perspective, science denial appears as a critique that is in tune with the times, insofar as it derives its plausibility from the current conditions of subjectification.
In the protest against established knowledge, the disappointed hope of the highly individualized, activated subject for complete sovereignty and a fully comprehensible, decision-open world is discharged. – (Bogner, 2021)
If politicians give knowledge absolute authority over political decisions, and these decisions realize certain values, the only way to fight for different values is to fight a different truth.
Using Bogner’s perspective, fake news are not the cause of the problem but a symptom of a society that feels impotent because certain values are always already presupposed to be the right values.
Therefore, what Bogner calls productive dissent becomes impossible.
The rebellion of the knowledge deniers can overall be understood as a covert appeal directed against a (looming) colonization of politics by expert consensus,
regardless of how reasonable the expert recommendations may be in individual cases. – (Bogner, 2021)
I agree with Bogner that a culture needs a common foundation, a reference world, which, according to Luhmann, should be provided by the media.
And we also need a more flexible and ambiguous reference world on a global scale, see (Bauer, 2018).
Furthermore, I agree that science cannot and should not realize politics and that better knowledge does not automatically lead to better politics.
Science should continue to operate on the true-false distinction, while politics should use a different code that differentiates values.
In case of climate activism, it might be a far more effective strategy to demand the values people want to be realized instead of discussing the facts they believe in.
Instead of calling people deniers, it might be healthier to find and employ strategies that reveal their value system and how this value system supports certain actions.
We should reinvigorate the discourse about values since it is save to say that more and better facts alone cannot move a society towards change.
However, I do not agree with Bogner’s claim that we need to agree that there is an objective truth to be found.
I even suspect he does not fully believe this himself, as he refers to the idea of an objective truth as a necessary fantasy, akin to Plato’s noble lie—a myth knowingly propagated by an elite to maintain social harmony.
I reject this in favor of an embracing uncertainty because, as I argued above, I think it drives the individual deeper into the cave.
As the philosopher Slavoj Žižek argues—contrary to Dostoevsky and many others—–that the belief in God enables us to commit horrific crimes, believing in an objectively accessible truth can serve the same purpose.
If we no longer live in the same world, society might break, but this does not diminish the great value of doubt and uncertainty in restraining our tendency for megalomania.
On this matter, I lean more towards Rorty, believing that we are mature enough to handle the pragmatist view that it is socially more useful to reject the idea of an objective truth (in the Platonist sense).
According to Rorty, Pippi Longstocking should be allowed to argue for her position, and we should accept her position to be true if it emerges out of the struggle for truth.
The American pragmatist rejects the Platonist’s notion of truth, considering it unintelligible and meaningless.
For the idea of a liberal society, it is of central importance that everything is allowed as long as it pertains to words as opposed to actions, to persuasion as opposed to violence.
This openness should not be maintained because, as the Bible says, the truth is great and will prevail, nor because, as Milton believes, in a free and open fight, the Truth will always win. A society is liberal when it is content to call ‘true’ whatever emerges as the result of such struggles. – (Rorty, 1098)
Many, including Bogner, believe that such an attitude leads to indifference.
He argues that if we take Rorty’s comment literally, we would bury both the idea of objective truth and our liberal democracy, since the realization of individual freedom through social change requires productive dissent.
I think Bogner, like many others, misinterprets Rorty or at least applies his statement to the wrong level of society—the wrong reality, so to speak.
The implication that we end up in a sort of absolute relativism or complete indifference if we stop believing in an objective truth remains unfounded.
It’s a huge leap.
Even if we reject the idea of an objective truth, empirical evidence is still valuable for discussions.
Rejecting the belief in an objective truth does not mean that we lose the ground for productive dissent.
On the contrary, it allows for a more pragmatic approach to dialogue and disagreement.
When we drop this belief, we recognize that our conversations and disagreements are grounded in our contingent vocabularies and cultural practices.
This recognition does not lead to indifference but rather to a greater appreciation of the diversity of perspectives.
It encourages us to engage with others’ values and beliefs not because they correspond to an objective reality, but because they are part of the shared human experience.
Productive dissent arises from the acknowledgment that our beliefs and values are fallible and open to revision through conversation.
It promotes a kind of solidarity where we strive to understand and negotiate our differences rather than impose a supposed objective truth.
This process fosters mutual respect and a more inclusive society, where different viewpoints can coexist and contribute to a richer, more nuanced understanding of the world.
By focusing on the practical consequences of our beliefs and actions, we can still engage in meaningful debates about what kind of society we want to create.
This pragmatic approach encourages us to find common ground and work together to address shared problems, rather than being paralyzed by the quest for an elusive objective truth.
Conclusion
What I wanted to emphasize is the idea that we are existing within a subjective and distorted world of a reality that we can not directly access.
We are always already in a simulation, relying on second-order observation.
What I call angry media outlets, many of which take part in spreading misinformation and conspiracy theories, use more and more frequently phrases like literally, this is simply the truth, they all know it, its a fact.
They fight against ambiguity dragging anything into a culture war such that it has to be defined using one of two perspectives.
Thus the root cause of descending into the rabbit hole may not be a detachment from reality but rather an attachment to certainty.
Perhaps Baudrillard is correct in asserting that we are entering a hyperreality that is no longer contradictory and dissolves all illusions, imaginations, and mysteries.
According to him, what we are trying to do is to purge the world of all mysteries, illusions and imaginations.
But certainty exists only in a pure form of simulation.
In a constructivist sense, we cannot access the absolute true reality (Kant’s the thing in itself) because it is always already mediated.
If we cannot accept this fundamental ambiguity of our reality (by which Baudrillard does not mean physical reality but that which is intelligible via signs), we run the risk of constructing the one and only reality, i.e., hegemony.
Since this realm does not allow contradictions, it tends to integrate everything, including disasters, into it.
Contradictions form the very foundation of our environment.
We perceive the reality of nature when it manifests as a non-human force of destruction, such as a natural disaster or a pandemic.
What occurs is incomprehensible.
In hyperreality, nature ceases to be a conflicting force and becomes merely an element within the simulation—a floating sign.
Destruction transforms into a calculated event.
Repeatedly displaying graphs of death tolls gives us the illusion of control.
It can be seen as an attempt to reintegrate death (arguably the greatest contradiction of all) into the simulation.
The negative, along with contradictions, is either integrated or discriminated against.
Wars, natural disasters, and pandemics metamorphose into a spectacle on the television screen, a tourist attraction for our theme park, and are more disastrous than the disaster, more natural than nature—in short, a perfect simulation that surpasses and supplants reality.
In a postmodern society, the absence of any central value system and firm, objective evaluative guides tends to create a demand for substitutes.
These substitutes are symbolically created rather than being actual or socially produced.
The need for these symbolic group tokens results in tribal politics and defines self-constructing practices that are collectivized but not socially produced.
These neo-tribes function solely as imagined communities and, unlike their premodern namesake, exist only in symbolic form through the commitment of individual ‘members’ to the idea of an identity.
They exist as imagined communities through a multitude of agent acts of self-identification and endure solely because people use them as vehicles of self-definition; as an identity technology termed profilicaty.
I have no intention of passing moral judgment on conspiracy theorists.
They often risk a significant amount of social capital, leading to alienation from their relatives and friends.
Being a conspiracy theorist is generally not an enjoyable experience.
As I said, they rebel against authority via the same use of authority—a conflict of knowledge against ‘better’ knowledge in the realm of politics.
This is dangerous.
It points to a deeper problem of a violation of the operational clousure of social systems which we should take serious if our goal is to preserve these systems.
One might even argue that conspiracy theorists perceive cracks in the simulation but mistakenly believe in a way out of it, which, and this misinterprets The Matrix as well, serves as the perfect cover-up for our reality as always partly simulated.
Baudrillard famously argued that Disneyland does not hide the fact that it is a simulation, but rather conceals the fact that America is a simulation too.
Disneyland is more real than America.
Conspiracy theories operate similarly; they are pure simulations and, in this regard, true.
The outsider is convinced of his or her reality, and the contradictory nature of these theories is not contradictory for him or her.
Instead, (obvious) contradictions are necessary to make the theory hyperreal.
The suspicion of the theorists is not unreasonable, but their conclusion is fatal—they demand a simple metanarrative and cannot see that this can only be another far more harmful simulation.
Several factors contribute to the prevalence of conspiracy theories, including information overload, the perception of a reality that is becoming ‘less real’, the sensation of living in a quasi-simulated reality, natural disasters, ongoing conflicts, and the rapid pace of our society.
Our modern world is so complex that it is virtually impossible for any single individual to comprehensively make sense of all that occurs.
As a result, we heavily rely on the concept of second-order observation, and there is no shame in acknowledging this fact.
Turning to experts and authorities, provided that their authority is derived from genuine competence, is necessary.
However, it’s crucial to subject these authorities to scrutiny and verification and to be aware that their observation has always a blind spot.
Nothing in what I’ve stated here should be misconstrued as a defense of the political system.
Lobbyism, which is sometimes indistinguishable from outright corruption, represents a significant issue.
The consistent failure to fulfill promises, whether they be pledges for a transaction tax, the cessation of subsidies that actively contribute to global warming, or the numerous ‘conferences’ like COP that, at this point, are merely part of a hope economy—offering a false and pacifying sense of hope—that fuels the distrust in institutions.
In my view, COP28 proved to be a disaster for the majority of the world’s population.
There was essentially no consensus on even the most basic measures.
No accord on phasing out fossil fuels, and not even a genuine commitment to promoting renewable energy.
The decision to have COP led by one of the world’s largest oil and gas companies is, at this point, satirical if it were not true.
In an assessment by journalist Jonathan Watts in The Guardian, the winners of the conference were identified as the oil and gas industry, the United States, China, COP28 President Sultan Al Jaber, the green energy sector, and lobbyists. Conversely, the losers encompassed the climate, small island nations, climate justice, future generations, other species, and scientists.
Nothing in what I’ve said here should be interpreted as a defense of the media for its issues, nor should it downplay the problem of increasing wealth inequality or any other ecological, social, or economic problems.
Both mass media and the scientific system have their problems, but this doesn’t negate their incredible value.
Moreover, independent media outlets play a crucial role, but we must be under no illusion that the verification of information is becoming increasingly challenging.
Social media platforms present us with an overwhelming array of viewpoints, claims, and video content. With the ascent of generative artificial intelligence, the task of verifying this deluge of information becomes even more daunting.
The power of the image is indeed huge.
The blurred line between hyperreality and lower forms of simulations makes it difficult to navigate through the mass of information. In contrast, conspiracy theorists do not bear the burden of a demanding verification process.
They can simply draw upon fringe and unvalidated stories, presenting them in an entertaining, sensational style akin to news pornography.
They can use the power of high-order simulacra which are disconnected from the real.
Believing in a conspiracy theory is akin to being the prisoner in Plato’s cave, presuming that everyone else is, in fact, in prison.
It is the belief in something outside of simulation.
The most effective remedy is to harbor doubts about our own competence, to be skeptical of ourselves, to maintain self-awareness at a metacognitive level, and to be able to live in a contradictory world and recognize those contradictions.
These contradictions live on the borders of hyperreality—in slums, cobalt mines, the streets of New York City, the border of Mexico, the fortress of the European sea, refugee camps, and the ‘ugly’ parts of the world.
I am not sure if I can agree with the cynical viewpoint of Baudrillard.
His overly dramatic and playful writings are interesting but also contradictory, probably by design.
He would probably be horrified at our attempt to simulate the whole earth to predict and control our future.
But how else can we deal with an open, unpredictable future other than the pursuit of more and more accurate predictions? Esposito asks if this future will still be open (Esposito, 2024; Esposito et al., 2023).
It appears to me that logical reasoning and providing ‘better’ facts alone is not sufficiently compelling.
Science and technology is not enough.
It feels like we lack spiritual growth.
Maybe Rorty is right about the importance of empathic stories.
Maybe science should provide us with that what we call truth and politics should offer us a story that moves us.
But where are these stories?
Are we already as cynical as Baudrillard?
We need storytellers and artists to craft more persuasive mythologies, narratives, and stories that resonate on an emotional level.
I believe this can only be possible if we do not filter out the negative and the ugly part of society.
We have to be serious yet playful and imaginative.
I want a serious vision which is shamelessly emphatic towards all forms of life.
This anti-Platonistic approach, while potentially controversial, could prove more effective in influencing beliefs and behaviors and, in the end, matter more than any rational argument could be.
We have reached an alarming point at which millions of people can no longer discriminate between reality and hyperreality.
That which cannot be simulated seems to disappear.
There is a confusion between truth claims grounded in evidence and sound logic and alternative facts inspired by an authoritarian rebellion against the authority of knowledge.
Even in the case of the climate crisis, if we want to preserve a liberal democracy, politics has to discuss alternatives based on the consideration of different values.
We need imagination to draw larger circles and rationalty to make valid moves within these circles.
We have to trust in the scientific method to provide us with good knowledege, politics (not politicians) that is informed by science to provide us with good politics, and spirituality that may spend us wisdom and psychologic stability.
Most importantly, instead of appealing to objective truth, it is more productive to focus on the practical consequences and shared values that can mobilize action.
Instead of arguing that climate change is an objective truth that everyone must accept, we should emphasize the practical and tangible consequences of climate inaction.
By highlighting concrete consequences, we may make a compelling case for action based on the observable and lived experiences of people.
We should frame the argument for climate action in terms of shared values and common interests.
The goal is to find common ground and motivate people to act based on their own interests and values, rather than trying to convince them of an abstract objective truth.
Acknowledging the contingency and fallibility of our beliefs does not mean we cannot act decisively.
We can adopt policies and actions that are based on the best available evidence while remaining open to revising them as new information emerges.
While rejecting objective truth might complicate the traditional ways of arguing for action, it also opens up new avenues for persuasion and coalition-building.
Sooner or later the reality of the crisis will eventually bleed into hyperreality.
Even if we construct our own perspective on the world, the reality of the climate crisis will not disappear if we stop believing in it.
References
- Popper, K. (1934). Logik der Forschung.
- Barthes, R. (1973). Mythologies. Hill & Wang Pub.
- Baudrillard, J. (1983). Simulacra and Simulation. Semiotext(e).
- Luhmann, N. (2000). Why does society describe itself as postmodern. In W. Rasch & C. Wolfe (Eds.), Observing complexity: Systems theory and postmodernity (pp. 35–49). University of Minnesota.
- Baudrillard, J. (1968). System of Objects.
- Baudrillard, J. (2008). The Perfect Crime. Verso.
- Douglas, K. M., Sutton, R. M., & Cichocka, A. (2017). The psychology of conspiracy theories. Current Directions in Psychological Science, 26(6), 538–542. https://doi.org/10.1177/0963721417718261
- Uscinski, J. E. (2018). The study of conspiracy theories. Argumenta, 233–245. https://doi.org/10.23811/53.arg2017.usc
- Prooijen, J.-W. (2018). The Psychology of Conspiracy Theories. Taylor & Francis Group. https://doi.org/10.4324/9781315525419
- Kay, J. (2011). Among the Truthers: A Journey Through America’s Growing Conspiracist Underground. Harper.
- Shermer, M. (2022). Conspiracy: Why the Rational Believe the Irrational. Johns Hopkins University Press.
- Landau, M. J., Kay, A. C., & Whitson, J. A. (2015). Compensatory control and the appeal of a structured world. Psychol Bull. https://doi.org/10.1037/a0038703
- Cichocka, A., Marchlewska, M., & Biddlestone, M. (2022). Why do narcissists find conspiracy theories so appealing? Curr Opin Psychol. https://doi.org/10.1016/j.copsyc.2022.101386
- Cosgrove, T. J., & Murphy, C. P. (2023). Narcissistic susceptibility to conspiracy beliefs exaggerated by education, reduced by cognitive reflection. Front Psychol. https://doi.org/10.3389/fpsyg.2023.1164725
- Hart, J., & Graether, M. (2015). Something’s going on here: Psychological predictors of belief in conspiracy theories. Journal of Individual Differences.
- Herman, E. S., & Chomsky, N. (1988). Manufacturing Consent. Pantheon Books.
- Maturana, H. R., & Varela, F. J. (1987). The Tree of Knowledge. Shambhala.
- Gabriel, M. (2018). Der Sinn des Denkens. Ullstein Buchverlag.
- Rorty, R. (2016). Philosophy as Poetry. University of Virginia Press.
- Sapolsky, R. M. (2023). Determined. Bodley Head.
- Arrhenius, S. (1896). XXXI. On the influence of carbonic acid in the air upon the temperature of the ground . The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 41(251), 237–276. https://doi.org/10.1080/14786449608620846
- Manabe, S., & Wetherald, R. T. (1967). Thermal equilibrium of the atmosphere with a given distribution of relative humidity. Journal of Atmospheric Sciences, 24(3), 241–259. https://doi.org/10.1175/1520-0469(1967)024<0241:TEOTAW>2.0.CO;2
- Keeling, C. D., Bacastow, R. B., Bainbridge, A. E., Ekdahl Jr., C. A., Guenther, P. R., Waterman, L. S., & Chin, J. F. S. (1976). Atmospheric carbon dioxide variations at Mauna Loa Observatory, Hawaii. Tellus, 28(6), 538–551. https://doi.org/10.1111/j.2153-3490.1976.tb00701.x
- Held, I. M., & Soden, B. J. (2006). Robust responses of the hydrological cycle to global warming. Journal of Climate, 19(21), 5686–5699. https://doi.org/10.1175/JCLI3990.1
- Weart, S. R. (2008). The Discovery of Global Warming. Harvard University Press.
- Myers, K. F., Doran, P. T., Cook, J., Kotcher, J. E., & Myers, T. A. (2021). Consensus revisited: quantifying scientific agreement on climate change and climate expertise among Earth scientists 10 years later. Environmental Research Letters, 16(10), 104030. https://doi.org/10.1088/1748-9326/ac2774
- Lynas, M., Houlton, B. Z., & Perry, S. (2021). Greater than 99% consensus on human caused climate change in the peer-reviewed scientific literature. Environmental Research Letters, 16(11), 114005. https://doi.org/10.1088/1748-9326/ac2966
- Cook, J., Oreskes, N., Doran, P. T., Anderegg, W. R. L., Verheggen, B., Maibach, E. W., Carlton, J. S., Lewandowsky, S., Skuce, A. G., Green, S. A., Nuccitelli, D., Jacobs, P., Richardson, M., Winkler, B., Painting, R., & Rice, K. (2016). Consensus on consensus: a synthesis of consensus estimates on human-caused global warming. Environmental Research Letters, 11(4), 048002. https://doi.org/10.1088/1748-9326/11/4/048002
- Cook, J., Nuccitelli, D., Green, S. A., Richardson, M., Winkler, B., Painting, R., Way, R., Jacobs, P., & Skuce, A. (2013). Quantifying the consensus on anthropogenic global warming in the scientific literature. Environmental Research Letters, 8(2), 024024. https://doi.org/10.1088/1748-9326/8/2/024024
- Doran, P. T., & Zimmerman, M. K. (2009). Examining the scientific consensus on climate change. Eos, Transactions American Geophysical Union, 90(3), 22–23. https://doi.org/https://doi.org/10.1029/2009EO030002
- Danaher, J. (2016). The Threat of Algocracy: Reality, Resistance and Accommodation. Philosophy & Technology, 29, 245–268. https://doi.org/10.1007/s13347-015-0211-1
- Bogner, A. (2021). Die Epistemisierung des Politischen. Reclam.
- Bauer, T. (2018). Die Vereindeutigung der Welt (p. 104). Reclam.
- Rorty, R. (1098). Contingency, Irony, and Solidarity (p. 201). Cambridge University Press.
- Esposito, E. (2024). Can we use the open future? Preparedness and innovation in times of self-generated uncertainty. European Journal of Social Theory, 0(0). https://doi.org/10.1177/13684310231224546
- Esposito, E., Hofmann, D., & Coloni, C. (2023). Can a predicted future still be an open future? Algorithmic forcasts and actionability in the precision medicine. History and Theory. https://doi.org/10.1111/hith.12327
]]>