Replacing Code with ML Models

This blog post aims to explore how machine learning can empower creative practitioners to bring to life projects that traditionally demanded significant technical expertise, such as programming skills. To make my case immediately understandable, I will provide a specific example. However, it’s worth noting that this is just one of countless possible instances.

You can find all the necessary code in my GitHub repo: link.

The example is based on the Wekinator, which is a powerful, free, and open-source software designed to simplify the process of using machine learning models. With its user-friendly interface, anyone can easily build new musical instruments, gestural game controllers, computer vision, computer listening systems, and much more. Developed by Rebecca Fiebrink, the software aims to make digital systems more accessible to artists and musicians. Although Wekinator’s initial release (version 1.0) dates back to 2009, the software remains relevant today and has aged gracefully.

In her article (Fiebrink, 2019), Fiebrink elaborates on her machine learning education practices for creative practitioners and highlights the benefits of using Wekinator. More recently, she has been working on a new tool called InteractML, which is a more advanced tool for interactive machine learning via visual scripting with Unity (Hilton et al., 2021). InteractML is a fascinating project that I plan to explore further at a later time. It is worth noting that the project is currently in alpha release and may only have limited documentation available.

One of the key advantages of the Wekinator is its ease of use, making it accessible to a wide range of users. The software’s versatility is due to its ability to open sound control (OSC) messages, which are supported by numerous applications, especially in the artistic domain. If other systems can communicate via OSC, they can be integrated (via network) into the larger system. For instance, most digital audio workstations (DAWs), Processing (a renowned creative coding environment), TouchDesigner, Max/MSP, PureData, SuperCollider and APIs for popular programming languages support OSC.

To demonstrate the potential of the Wekinator, I will be using Processing and SuperCollider, both of which are also free and open-source tools. SuperCollider will be used to generate sound, while Processing will capture human motion. The objective is not to showcase elaborate gesture recognition but to provide an overview of the Wekinator’s fundamental workings.

More than just discussing the Wekinator, my aim is to provide readers with an understanding of how machine learning can supplant traditional programming, enabling non-experts to utilize techniques that were previously inaccessible to them.

We will observe how machine learning can replace coding, albeit with some coding required. However, the coding required is specific to the task of sending and receiving OSC messages, and the tools utilized, i.e., SuperCollider and Processing which are both programming environments. Other tools exist, which allow for sending OSC messages without any coding, and there are tools that produce sound without programming.

The following video demonstrates the final result and all the steps required.

Problem Description

Digital synthesizers are synthetic instruments that generate sound by outputting a stream of floating point numbers. These synthesizers typically have numerous parameters, such as frequency (pitch), cutoff frequency of a low-pass filter, frequency of the carrier, and several others. Often these parameters are not interpretable, meaning there is no straightforward connection between a parameter and the sound a synth generates. Instead, altering multiple parameters concurrently leads to the desired outcome. In mathematics, we refer to these parameters as residing in a high-dimensional space.

Let’s consider the following scenario: We have a dancer in a rectangular area, such as a room, and we wish to modify the sound generated by a synth based on the dancer’s 2D position. We aim to alter the synth’s parameters while it is playing (modulation) in response to the dancer’s movements. However, the changes in sound must be smooth and non-random.

Unfortunately, a significant problem arises in this situation. The number of parameters exceeds the number of positional values. We only have two coordinates to work with, and establishing a one-to-one mapping between these coordinates and parameters is not feasible. We want to avoid merely selecting two parameters and modifying them according to the dancer’s $x$ and $y$ coordinates.

In mathematical terms, we are looking for a function that receives $2$ values ($x$ and $y$) and outputs $n$ values (one for each parameter), where $n > 2$. We want a function

\[f : \mathbb{R}^2 \rightarrow \mathbb{R}^n.\]

Additionally, it is necessary for $f$ to be smooth and meet our musical preferences. As $f$ maps a lower-dimensional space to a higher-dimensional space and we require a seamless transition, we search for a two-dimensional surface in an $n$-dimensional space. As the dancer moves in the $x$ and $y$ directions, $f$ translates this motion to a movement on the two-dimensional surface in the $n$-dimensional space.

If we have only one coordinate and three parameters, $f$ represents a curve in the three-dimensional space. In this case, we can draw it. Compare Fig. 1.

Figure 1: Sample points and fitted graph of a curve in a three-dimensional space. The length of the curve represents the dancer's single coordinate (let's say x). A point (X,Y,Z) on the curve represents three parameter values.

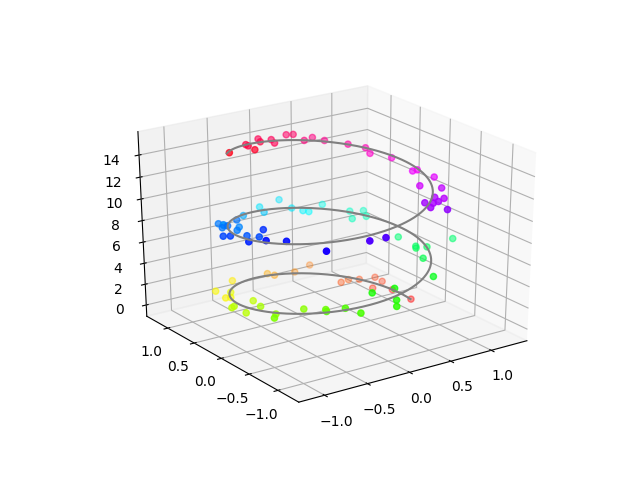
This is a complex challenge, and several questions arise: How does $f$ look like? How can we implement it?

Reasoning about the World

Before the advent of machine learning, we would have addressed this problem using the “traditional way” of abstract reasoning and programming to implement the function $f$ directly via code. This approach involves roughly six steps:

observer and analyse the system
construct a falsifiable mathematical model (which is an imperfect generalization)
implement a numerical model via code
calibrate the model
test your assumption via observation until the model approximates reality adequately
find unobserved phenomena, which the model implies, in the real world

Newton’s discoveries serve as a classic example, where he observed reality and reasoned about it, generating laws that are incorrect but sufficiently accurate to travel to the moon. He established formulas such as

\[F = m \cdot a,\]

which are falsifiable via experiments. With these formulas one can predict unknown phenomena that should appear if the model is reliable.

In our case, we would have conducted a comprehensive analysis of the synth to establish how its parameters interact with one another. This approach would have required a wealth of knowledge across diverse domains such as programming, signal processing, and mathematics. Furthermore, to achieve our desired sound, we would have needed to understand the impact of parameter changes on various aspects of the sound, such as pitch and timbre.

In essence, we would have aimed to create a model of the synth “world” to enable us to reason about its structures and rules. We would have then written code to manipulate the $n$ parameters concurrently, relative to the dancer’s position.

While I value the traditional approach for its ability to provide insights into actual and imaginative structures, it is not the optimal solution for our specific scenario. I believe that creative practitioners do not necessarily avoid analytical work but tend to focus on creation, thereby enabling a more tangible understanding of the problem. I welcome this approach, particularly in the field of machine learning. In contrast, the traditional approach can be challenging and less accessible, particularly in achieving our artistic objectives.

Modelling without Reasoning

In machine learning, the focus shifts to a data-driven approach. Rather than constructing a model by hand through reasoning about the world, we enable machines to learn the model by providing them with data, i.e., observations.

In extreme cases when observation is the model, we cannot provide outputs of unobserved inputs. Therefore, like models constructed manually, machine learning models are an imperfect abstraction of the data on which they are trained. This is the fundamental idea behind machine learning, albeit an oversimplification.

In our scenario, we replace manual modeling with machine learning by defining what we want and letting the machine learning models provided by the Wekinator figure out how to achieve it. We present an algorithm $A$ with examples $D$ that represent our requirements and ask it to “program” a function $f$ that fulfills our needs.

Machine learning involves learning $f$ from data $D$ using algorithm $A$, where $A$ is essentially just another function that produces functions:

\[A(D) = f\]

The Wekinator allows us to choose algorithm $A$ from a list of algorithms and provides a graphical user interface (GUI) for recording $D$ and feeding it into $A$ to compute $f$. The algorithm $A$ is predetermined, and $f$ will be computed. As a result, we need to provide data/observation $D$ by recording it, so let’s get started!

Disclaimer: Utilizing machine learning does not imply that we cease rationalizing about the world. However, I selected this thought-provoking title to accentuate the contrast in tendencies. Moreover, the effectiveness and characteristics of machine learning models are significantly influenced by the quality of the observed data and the choice of algorithm. Given that our challenge involves a regression task, we will employ a feed-forward neural network.

Realization

In the following, we have a lot to set up since every part of the system is digital and our own creation. However, do not worry if you do not understand the SuperCollider or Processing part. It is more important to understand the principle of OSC communication and the Wekinator. If you are interested in SuperCollider or Processing I can highly recommend checking them out.

Creating a new Instrument

First, we need an actual synthesizer that produces sound. I use a synth that randomly produces a short resonating impulse that gets reflected. I want to go into only a few details about the inner workings of the synth. It creates a sound similar to a firework in a city perceived inside a room.

The synth has 6 parameters which are, in this case, explainable:

\densityleft controls the number of impulses in the left speaker.
\densityright controls the number of impulses in the right speaker.
\freq controls the pitch of the impulse response (i.e., the sound). Higher frequency increases the pitch. (For Ringz it is the frequency at which the impulse resonates.)
\cutofffreq controls the cutoff frequency of the lowpass filter. Lower values make the sound more doll.
\decaytime controls the time it takes for the impulses to decay, influencing the resonance.
\amp controls the signal’s amplitude, i.e., the volume.

Dust outputs the impulse such that Ringz resonates. The resulting signal gets reflected by FreeVerb which introduces reverberation.

(
SynthDef(\fireworks,{
    var sig;
    sig = Dust.ar([\densityleft.kr(3), \densityright.kr(3)-0.5]);
	sig = Ringz.ar(
		sig, 
		freq: \freq.kr(300), 
		decaytime: \decaytime.kr(0.1)) * \amp.kr(0.55);
    sig = FreeVerb.ar(sig, 0.6, 0.9, 0.8);
    sig = LPF.ar(in: sig, freq: \cutofffreq.kr(21000));
    Out.ar(0, sig);
}).add;
)

We can play the synth and manipulate its parameters on the fly. Let’s listen but be warned since the amplitude during this example will change.

~fireworks = Synth(\fireworks);
~fireworks.set(\amp, 1);
~fireworks.set(\densityleft, 10);
~fireworks.set(\freq, 400);
~fireworks.set(\decaytime, 0.3);
~fireworks.free();

Ok cool, we can play sound.

Simulation of the Dancer

Next, let’s envision a dancer gracefully moving across the room. While I am not a dancer, nor do I possess sensors to measure a dancer’s position, we can simulate this scenario using Processing. It’s worth mentioning that we could achieve the same result with SuperCollider, as it also features GUI elements. However, I’d like to demonstrate how we can effortlessly integrate multiple systems.

You can download the Processing example at this link. I will provide the code below, but please don’t be intimidated. It simply consists of a draggable green square, accompanied by informative log text displayed on a black window, and an OSC sender. Dragging the green square simulates the dancer’s movement, while the application continuously transmits the rectangle’s central position over the network.

Figure 2: Running Processing sketch.

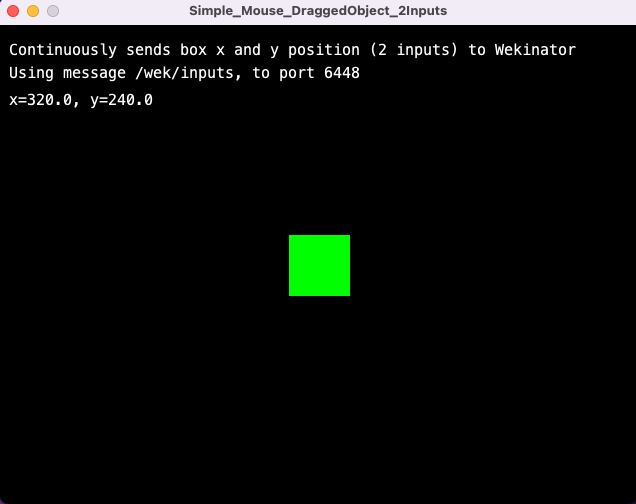
If you start the sketch in Processing, you should see the window shown in Fig. 2.

/**
* REALLY simple processing sketch that sends 
* mouse x and y position of box to wekinator
* This sends 2 input values to port 6448 using message /wek/inputs
* Adapated from https://processing.org/examples/mousefunctions.html 
* by Rebecca Fiebrink
**/

import oscP5.*;
import netP5.*;

OscP5 oscP5;
NetAddress dest;
PFont f;

float bx;
float by;
int boxSize = 30;
boolean overBox = false;
boolean locked = false;
float xOffset = 0.0; 
float yOffset = 0.0;

void setup() {
    f = createFont("Courier", 15);
    textFont(f);

    size(640, 480, P2D);
    noStroke();
    smooth();
    
    bx = width/2.0;
    by = height/2.0;
    rectMode(RADIUS);  
    
    /* start oscP5, listening for incoming messages at port 12000 */
    oscP5 = new OscP5(this,9000);
    dest = new NetAddress("127.0.0.1",6449);
}

void draw() {
    background(0);
    fill(255);
    text("x=" + bx + ", y=" + by, 10, 80);
    
    fill(0, 200, 0);

    // Test if the cursor is over the box 
    if (mouseX > bx-boxSize && mouseX < bx+boxSize && 
        mouseY > by-boxSize && mouseY < by+boxSize) {
        overBox = true;  
        if(!locked) { 
        stroke(0, 255, 0); 
        fill(0, 255, 0);
        } 
    } else {
        stroke(0, 255, 0);
        fill(0, 255, 0);
        overBox = false;
    }
    
    // Draw the box
    rect(bx, by, boxSize, boxSize);
    
    //Send the OSC message with box current position
    sendOsc();
}

void mousePressed() {
    if(overBox) { 
        locked = true; 
        fill(0, 255, 0);
    } else {
        locked = false;
    }
    xOffset = mouseX-bx; 
    yOffset = mouseY-by; 
}

void mouseDragged() {
    if(locked) {
        bx = mouseX-xOffset; 
        by = mouseY-yOffset; 
    }
}

void mouseReleased() {
    locked = false;
}

void sendOsc() {
    OscMessage msg = new OscMessage("/wek/inputs");
    msg.add((float)bx); 
    msg.add((float)by);
    oscP5.send(msg, dest);
}

When we start the Processing sketch, it shows a green square inside a black window. The window represents our room, and the green square the dancer. You can drag the dancer around.

OSC Communication

The only crucial part of the Processing sketch’s code is the transmission of OSC messages..

oscP5 = new OscP5(this,9000);
dest = new NetAddress("127.0.0.1",6448);

These three lines of code enable the sketch to listen for OSC messages over the network using the IP address "127.0.0.1", which represents the local IP address. This means that the sketch listens for messages originating from your device. It receives messages on port 9000 and transmits them to port 6448. The listening port is inconsequential, as the dancer never responds to incoming signals. The IP address and sending port are crucial because they must correspond with the numbers we will employ in the Wekinator.

The following code

void sendOsc() {
    OscMessage msg = new OscMessage("/wek/inputs");
    msg.add((float)mouseX); 
    msg.add((float)mouseY);
    oscP5.send(msg, dest);
}

sends the coordinates $x$ and $y$ of the mouse (with respect to the window) to the port 6448 and the path '/wek/inputs'. OSC uses these paths such that it is possible to differentiate different types of messages that got sent to some port.

Now we have to set up OSC communication of our sound generating system, i.e. SuperCollider. Let us first listen to port 6448and path '/wek/inputs' and let’s just print the raw data we perceive, i.e., the $x$ and $y$ values of our dancer (the green square).

(
OSCdef(
    \getCoords,
    {
        arg val; val.postln;
    },
    '/wek/inputs',
    recvPort: 6448
);
)

By executing this line in SuperCollider while the Processing sketch is running, you should see OSC messages on the post window. These messages look like this:

[ /wek/inputs, 248.0, 185.0 ]

Now, let’s take it a step further and modify two synth parameters based on these values. The following code maps $x$ and $y$ to a suitable range. While $x$ ranges from 0 to 650 and $y$ from 0 to 460, we aim to obtain values between 0.1 and 20.

(
OSCdef(
    \getCoords,
    {
        arg val; var x, y;
        x = val[1];
        y = val[2];
        ~fireworks.set(\leftdensity, x.linlin(0, 650, 0.1, 20));
        ~fireworks.set(\rightdensity, y.linlin(0, 460, 0.1, 20));
    },
    '/wek/inputs',
    recvPort: 6448
);
)

The impact of this code should be noticeable in the audio output. When the dancer is positioned at the top left, fewer impulses are produced. If situated at the bottom right, impulses emit from both speakers, while being at the bottom left results in only the right speaker activating. This effect may not seem extraordinary, as our function $f$ is quite elementary, involving a linear mapping from one interval to another.

The Machine in the Middle

We now introduce the Wekinator in the middle of the communication. That is, the dancer sends their position to the Wekinator, and SuperCollider listens to the messages from the Wekinator and changes the values of the synth accordingly. The Wekinator translates positions into synth parameters, and it realizes the function $f$. The 6 output signals

\[(v_1, \ldots, v_6) = f(x,y)\]

are sent to SuperCollider.

Figure 3: Overview of all the connected parts.

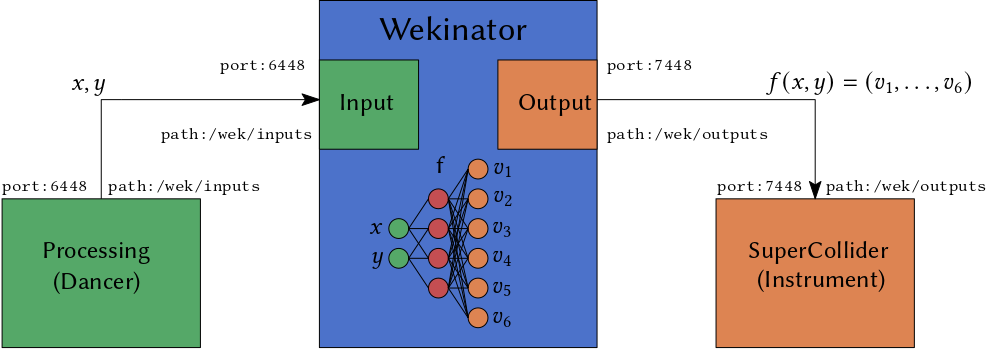
First, we need to modify the port SuperCollider listens to by changing the line from recvPort: 6448 to recvPort: 7448. Additionally, we should update the path to '/wek/outputs' as a reminder that we are receiving output signals from Wekinator.

Secondly, we must utilize the values we receive. Wekinator consistently sends a value between 0 and 1 for each dimension. As a result, we need to map the interval [0;1] to appropriate synth values. This step is critical and necessitates some understanding of the synth. I employ the following mapping (note that we skip val[0] since it represents the OSC path):

(
OSCdef(
    \getCoords,
    {
        arg val;
        ~fireworks.set(\densityleft, val[1].linlin(0, 1, 0.1, 20));
        ~fireworks.set(\densityright, val[2].linlin(0, 1, 0.1, 20));
        ~fireworks.set(\freq, val[3].linlin(0, 1, 100, 700));
        ~fireworks.set(\amp, val[4].linlin(0, 1, 0, 2));
        ~fireworks.set(\decaytime, val[5].linlin(0, 1.0, 0.01, 1.0));
        ~fireworks.set(\cutofffreq, val[6].linlin(0, 1, 200, 20000));
    },
    '/wek/outputs',
    recvPort: 7448
);
)

If you use SuperCollider be careful with your choices and protect your ears since it will try to use even unreasonable values like an amplitude of 10 or higher.

Now we start the Wekinator. First, we have to specify the port for the input signals of $f$, i.e., the dancer’s position. This is equal to 6448, and the OSC path is '/wek/inputs'. Then we have to specify the port of the output signal $f(x,y)$, i.e., the port used in SuperCollider, which is 7448 furthermore, we specify a path '/wek/outputs' such that we do not confuse input and output.

Figure 4: Wekinator after it has started.

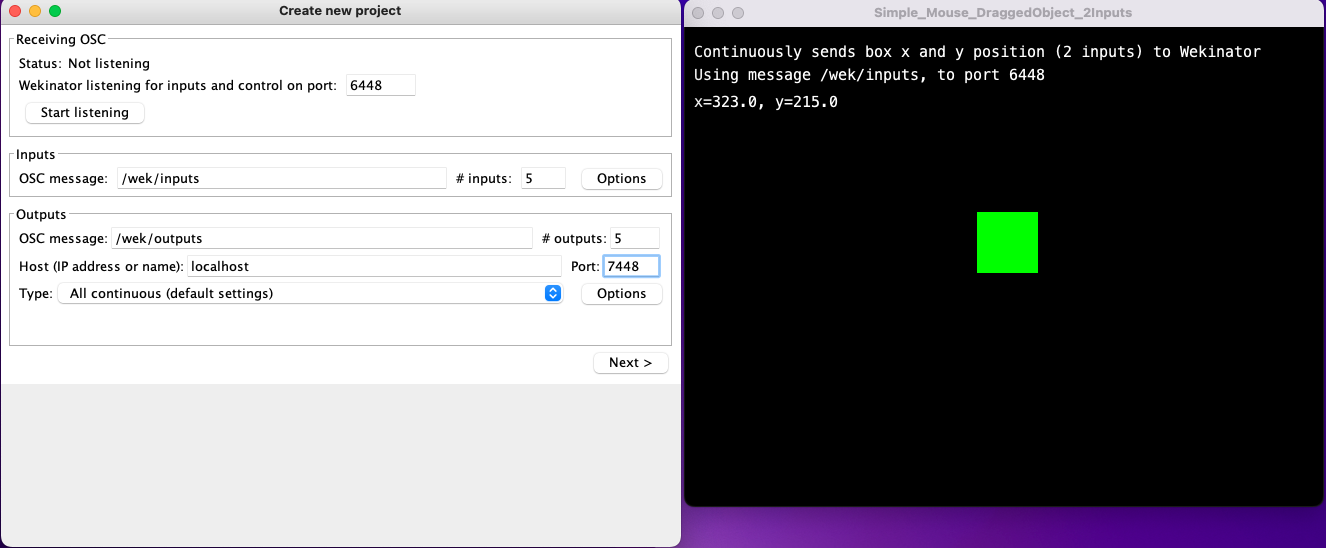
Furthermore, we have to tell the Wekinator about the number of inputs and outputs, i.e., 2 and 6, respectively. After everything is set up, we can click on Start Listening. Then we can click Next.

Now you will see the following screen. In the top left OSC In should be green, since the Processing sketch is sending messages.

Figure 5: Wekinator before training.

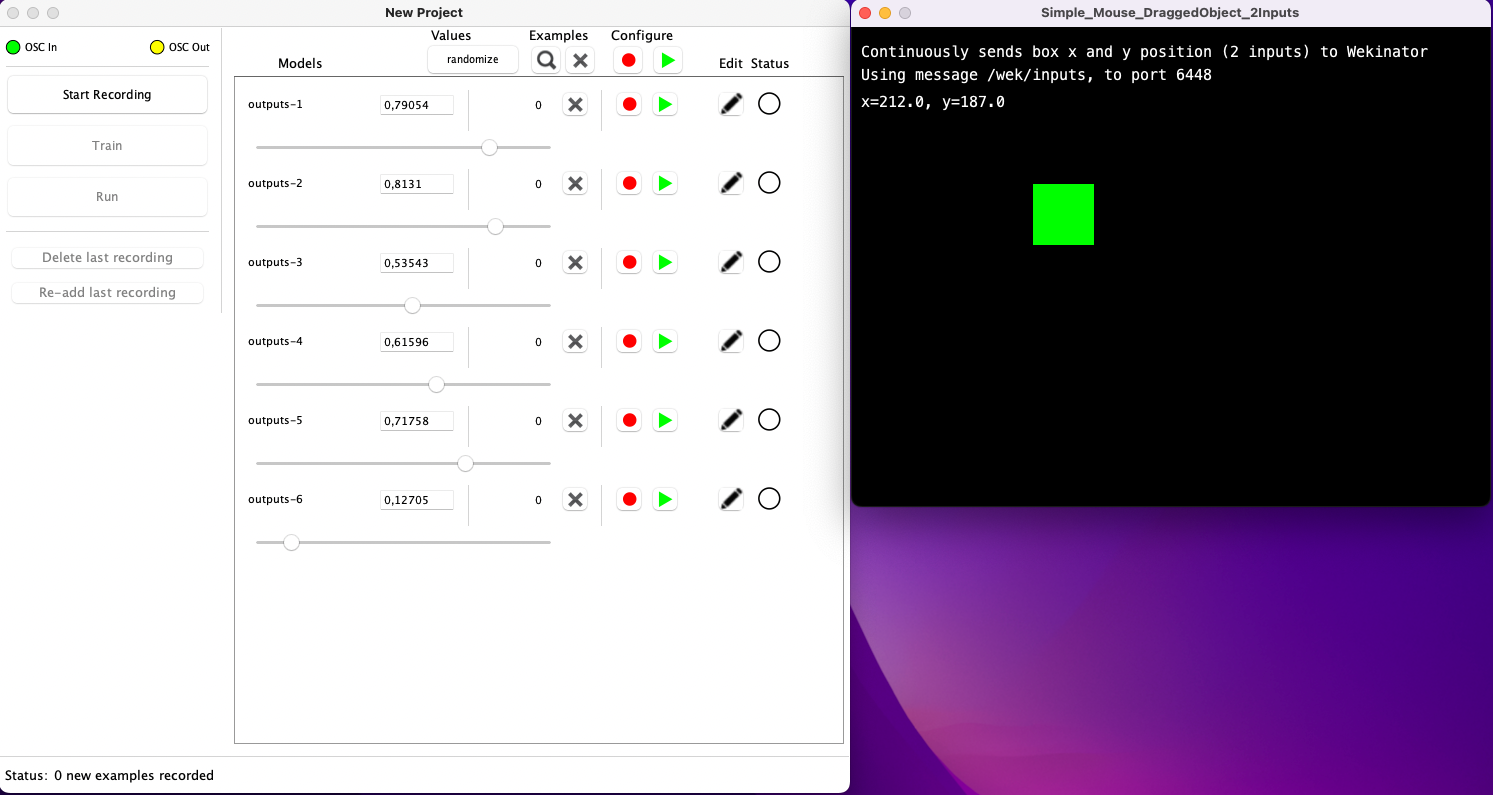
If this is not the case, you either forgot to click Start Listening, or the port is already used. In that case, change the port in the Wekinator as well in your Processing sketch and restart the sketch. You also should see 6 sliders. If you manipulate these sliders, OSC Out should turn green, indicating that we are sending OSC messages to SuperCollider.

Furthermore, the sound should change accordingly. Make sure your amplitude is not zero. Now you can play around with the sliders or press the random button until you hear something you like. Of course, you have to remember which slider represents which parameter.

To connect the sound to the dancer’s position, we have to

record samples, i.e., construct the data set $D$
train the model, i.e. compute $f = A(D)$.

To construct $D$ we need multiple tuples

\[(\text{input}, \text{output}) = ((x,y), (v_1, \ldots, v_6)).\]

First, we move the square to a desired position and choose a set of desired parameters $(v_1, \ldots, v_6)$. Next, we click Start Recording, and after a few seconds, we press Stop Recording. In doing so, we generate portions of the data $D$. We repeat this step multiple times until we have accumulated sufficient data $D$.

Once completed, we press Train to compute

\[A(D) = f.\]

This process should only take a few seconds.

Finally, we can utilize $f$ by clicking Run. At this point, both OSC In and OSC Out indicators should be green, and as you move the square around, the sound should change accordingly. Moreover, all parameters (assuming they were all manipulated during recording) should transition smoothly.

Different Algorithms

Keep in mind that we did not specify any algorithm A. By default, Wekinator employs a feed-forward neural network and assumes a regression task. This means that the output $f(x,y)$ is continuous and does not represent an element within a finite set of classes.

You can choose algorithms by modifying the Type setting, as shown in Fig. 4. This selection includes classification algorithms. For instance, if you wish to establish a mapping between a gesture captured by your webcam and a specific sample, this would be a classification task. Another example would be classifying the type of instrument being played.

Wekinator has some limitations regarding the range of algorithms it offers, as the user lacks control over the model architecture and the model’s hyperparameters.

Summary

Wekinator is an outstanding tool that makes certain aspects of machine learning accessible. Its compatibility with OSC allows for seamless integration into various systems. It is an ideal fit for quick experimentation and serves as a valuable tool for teaching creative practitioners the fundamentals of machine learning on an intuitive level.

However, it does feel somewhat dated and experimental, offering no control over the hyperparameters of its built-in models. Additionally, it does not utilize the latest software libraries, such as PyTorch or TensorFlow. Being a Java application, it supports all operating systems, but Java is a relatively uncommon programming language in the field of machine learning.

The concept behind Wekinator is exceptional, and it shouldn’t be too challenging to create a similar tool in Python, enabling artists or developers to integrate their own PyTorch or TensorFlow models. It supports the goal of making machine learning accessible to everyone and provides valuable insights into the features that ML tools for non-experts should offer. Perhaps we can develop new tools to break down even more barriers, allowing practitioners and developers to learn from one another.

In any case, if you’re interested in experimenting with simple machine learning models that process various types of generated input, give Wekinator a try.

References

Fiebrink, R. (2019). Machine learning education for artists, musicians, and other creative practitioners. ACM Trans. Comput. Educ., 19(4). https://doi.org/10.1145/3294008
Hilton, C., Plant, N., González Dı́az Carlos, Perry, P., Gibson, R., Martelli, B., Zbyszynski, M., Fiebrink, R., & Gillies, M. (2021). InteractML: Making machine learning accessible for creative practitioners working with movement interaction in immersive media. Proceedings of the 27th ACM Symposium on Virtual Reality Software and Technology. https://doi.org/10.1145/3489849.3489879