3.1. Symbole, Schrift und Zahlen

Zeichen sind das Herzstück jedes Algorithmus. Ein abstraktes Zeichen fungiert als Repräsentant für etwas anderes und schafft oftmals eine symbolische Gleichheit zwischen verschiedenen Objekten oder Prozessen. Nehmen wir als Beispiel das Wort ‚Stuhl‘. Es steht für eine Vielzahl von Objekten, die alle die gemeinsame Funktion erfüllen, nämlich eine Sitzgelegenheit zu bieten. Wörter sind im Grunde nichts anderes als Sequenzen von Zeichen, die einen speziellen Begriff repräsentieren. Interessanterweise ist dieser Begriff oftmals universell und nicht an eine bestimmte Sprache gebunden. Zum Beispiel weisen die Wörter ‚Stuhl‘ im Deutschen und ‚chair‘ im Englischen beide auf die gleiche zugrundeliegende Idee oder Vorstellung hin. Im weiteren Verlauf dieses Buchs, genauer gesagt im Kapitel Was ist Information?, werden wir diesen komplexen Zusammenhang detaillierter untersuchen.

Es ist wichtig zu verstehen, dass Zeichen—Wörter, Symbole oder Begriffe—die fundamentalen Bausteine sind, um Algorithmen in einem kulturellen Kontext weiterzugeben. Interessanterweise ist die spezifische Bedeutung eines Zeichens oder Wortes der natürlichen Sprache oft weniger eindeutig, als man denken könnte; sie ist in der Regel eine Frage der gesellschaftlichen Vereinbarung oder Konvention. Wörterbücher bieten zwar Definitionen an, aber bei genauerem Hinsehen sind diese für viele Wörter oft unvollständig.

Die tatsächliche Bedeutung eines Wortes entsteht vielmehr durch seinen Gebrauch in der Sprache. Und dieser Gebrauch ist kontingent; das bedeutet, er könnte auch anders sein. Die Bedeutung des Worts ‚Stuhl‘ ist nicht festgeschrieben, sondern entwickelt sich aus der Art und Weise, wie es von anderen verwendet wird. Diese Verwendung hat historische und kulturelle Wurzeln und ist einem ständigen Wandel unterworfen. Dabei ist sie jedoch nicht willkürlich, sondern folgt bestimmten Mustern und Regeln. Algorithmen unterscheiden sich dabei von Sätzen der natürlichen Sprachen, da sie eine exakte, eindeutige und beständige Definition besitzen. Dennoch begann alles mit der natürlichen Sprache.

3.1.1. Entwicklung der Schrift

Die Ursprünge der Sprache sind ein Mysterium, das wir wahrscheinlich nie vollständig entschlüsseln können. Bei der Entwicklung der Schrift haben wir hingegen deutlich mehr Anhaltspunkte. Der Beginn liegt in der Verwendung von sogenannten Logogrammen, grafischen Zeichen, die jeweils bestimmte Wörter oder Ausdrücke in der Sprache darstellen. Interessant ist, dass Logogramme in verschiedenen Formen und Kategorien auftreten können:

1. Bildsymbole: Diese sind grafische Darstellungen, die dem Gegenstand, den sie repräsentieren, ähneln.

2. Begriffszeichen: Diese Symbole repräsentieren abstrakte Ideen und fungieren als Träger ihrer Bedeutung.

3. Lautzeichen: Diese stehen für spezielle Sprachlaute oder Silben.

Das Einzigartige an Logogrammen ist, dass sie in der Regel einen kompletten Begriff darstellen und, anders als in reinen Bilderschriften, meistens aus einer Kombination mehrerer logographischer Zeichen bestehen.

Mit der Zeit entwickelten sich aus Logogrammen häufig Silbenschriften. Dieser Wandel wurde durch den Prozess der Phonetisierung begünstigt, bei dem bestimmte Zeichen mit spezifischen Lauten oder Silben verknüpft wurden. Solche Silbenschriften können dann die Basis für ein Alphabet bilden, auch wenn dies nicht immer der Fall ist. Das chinesische Schriftsystem, zum Beispiel, basiert nach wie vor auf Logogrammen. Ein Übergang zu einem alphabetischen System findet hauptsächlich bei Sprachen statt, die sich in ihre grundlegenden Komponenten zerlegen lassen.

Das älteste uns bekannte vollständig entwickelte Schreibsystem entstand um 3000 v. Chr. in Mesopotamien und Ägypten. Ursprünglich basierten diese Systeme auf bildlichen Darstellungen, die mit der Zeit immer abstrakter wurden. Die oft komplexen Hieroglyphen wurden etwa vereinfacht und in die sogenannte hieratische Schrift (3200 v. Chr. bis 394 n. Chr.) überführt. Aus dieser entstand durch weitere Abstraktion die demotische Schrift (650 v. Chr. bis 450 n. Chr.).

Diese fortschreitende Abstraktion legte den Grundstein für das Computational Thinking. Menschen konnten nun Objekte durch Symbole oder Sequenzen von Symbolen repräsentieren, was ihnen ermöglichte, abstrakte Operationen mit diesen Objekten auszuführen, ohne sie physisch zu manipulieren. Das hat das Potenzial der menschlichen Kognition wesentlich erweitert.

3.1.2. Entwicklung der Zahlensysteme

Ein praktisches Beispiel für solch eine abstrakte Operation ist das Zählen. Hier steht ein Symbol, das wir als Zahl bezeichnen, für die Existenz einer bestimmten Anzahl von Objekten. Ein Zahlensystem definiert dann, wie diese Zahlen dargestellt werden, insbesondere wenn die Anzahl der repräsentierten Objekte nicht sofort erkennbar ist—wie etwa die Punkte auf einem Würfel. Im Laufe der Geschichte gab es dabei effektive und weniger effektive Zahlensysteme, je nachdem, wie gut sie sich für die Durchführung von Berechnungen mittels Symbolmanipulationen eigneten.

Der Zeitpunkt, an dem Menschen zu zählen begannen, ist ein immer noch nicht gelöstes Rätsel. Es existieren jedoch faszinierende Indizien, beispielsweise in Form von Gravuren auf Knochen, die darauf hindeuten könnten, dass unsere Vorfahren schon vor rund 35.000 Jahren damit anfingen, Zählvorgänge mithilfe von Markierungen festzuhalten.

Ein effizientes Zahlensystem erfordert eine hohe Abstraktionsleistung und baut oft auf einer bestimmten Basis auf. Historisch betrachtet haben sich insbesondere Systeme mit den Basen 5, 10 und 20 durchgesetzt. Dies liegt wahrscheinlich daran, dass wir fünf Finger an einer Hand und insgesamt zehn Finger und Zehen haben. Heutzutage dominiert das Dezimalsystem, obwohl in einigen Sprachen, wie dem Französischen und Dänischen, noch Spuren von Systemen mit der Basis 20 zu finden sind.

Wenn wir die Entwicklung von Zahlensystemen im historischen Kontext betrachten, lassen sich zwei grundlegende Prinzipien der Systematisierung identifizieren: Entweder bauen die Systeme auf einer kumulativen Addition von Symbolen für verschiedene Werte auf—bekannt als Additionssystem—oder sie definieren den Wert der Symbole durch ihre Position im System, das als Stellenwertsystem bezeichnet wird. Ein einfaches Beispiel für ein Additionssystem ist die klassische Strichliste, ein Unärsystem, das nur ein Symbol nutzt und dessen Wert durch die Anzahl der wiederholten Symbole bestimmt wird. Das römische Zahlensystem ist ein weiteres bekanntes Beispiel für ein Additionssystem, in dem die Addition einfach, aber andere Berechnungen oft umständlich sind.

Das erste vollständige und uns bekannte Zahlensystem wurde von den Sumerern um 3000 v. Chr. entwickelt. Es handelte sich dabei um ein Additionssystem, das später von der babylonischen Mathematik ab etwa 2000 v. Chr. in ein Stellenwertsystem umgewandelt wurde. Dieses basierte auf der ungewöhnlichen Basis von 60 und wird daher als Sexagesimalsystem oder Sechziger-System bezeichnet. Es findet heute noch Anwendung in der Angabe von Winkeln und geografischen Koordinaten. Interessanterweise verwendeten die Babylonier nur zwei Symbole: eines für die ‚1‘ und eines für die ‚10‘. Bis zur Zahl 60 wurde additiv gezählt; danach kamen positionelle Überlegungen ins Spiel. Zum Beispiel wird die Zahl 62 durch drei positionierte Zeichen dargestellt: eine ‚1‘ an der vorderen Stelle, die für 60 steht, und zwei ‚1er‘ an der hinteren Stelle für die verbleibende ‚2‘.

Eine weitere interessante Zahlennotation erfand die südamerikanische Bevölkerung des Inkareichs. Diese Notation ist unter dem Namen Khipu oder Quipu bekannt. Der Name Khipu (spanisch: Quipu, quechua: Khipu) bedeutet Knoten und steht sowohl für den einzelnen Knoten, als auch für das gesamte Gebilde aus Knotenschnüren. Mit dieser Knotenschrift lassen sich komplexe Informationen codieren. Die Inkas stellten damit mehrstellige Zahlen im Dezimalsystem dar. Nach heutiger Erkenntnis gab es zwei verschiedene Schriftsysteme: eines zur Erfassung von Mengen von Lagerbeständen, Menschen, Tieren, Pflanzen und Ländereien, und eines für Nachrichtenverkehr, wie Briefwechseln. Dieses System erweitert unsere Vorstellung davon, wie Informationen erfasst und kommuniziert werden können, und zeigt die Vielfalt der Methoden, die Menschen im Laufe der Geschichte entwickelt haben.

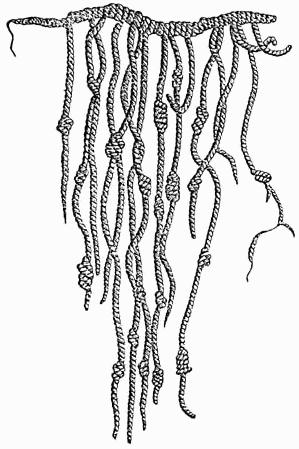
Abb. 3.1 Beispiel eines Khipu.

Das ägyptische Zahlensystem entstand im alten Imperium um ca. 2700-2200 v. Chr. Dieses hieroglyphische Zahlensystem ist ein dezimales Additionssystem. Eine aufgeschriebene Zahl beginnt von rechts nach links mit dem kleinsten Symbol und die Symbole werden nach links hin immer größer. Es scheint fast so als würde die Position der Symbole eine Rolle spielen, jedoch ist der Wert der repräsentierten Zahl gleich der Summe aller Werte der einzelnen Symbole. Somit spielt die Position eigentlich gar keine Rolle.

Das heute am weitesten verbreitete Zahlensystem ist das hindu-arabische oder indo-arabische Stellenwertsystem. Entwickelt wurde es zwischen 100 und 400 n. Chr. in Indien und fußt vermutlich auf den chinesischen Zahlzeichen aus dem Jahr 1200 v. Chr. Das chinesische System kombiniert Elemente von Additions- und Stellenwertsystemen und basiert ebenfalls auf Dezimalzahlen. Obwohl das System ursprünglich aus Indien stammt, wird es oft als arabisches oder persisches System bezeichnet, da es von arabischen Händlern nach Europa gebracht wurde. Das System umfasst neun Basiselemente: die Ziffern 1 bis 9. Doch was ist mit der Null?

Die Geschichte der Null ist eine faszinierende Reise durch verschiedene Kulturen und Zeitalter. Während das Konzept der Null in unterschiedlichen antiken Zivilisationen wie den Babyloniern und den Mayas existierte, nahm die Null in ihrer heutigen Form erstmals in Indien Gestalt an. Man nimmt an, dass die Eroberungen Alexanders des Großen das babylonische Zahlensystem nach Indien brachten, wo es weiterentwickelt wurde. Einer der größten Beiträge indischer Mathematiker*innen war die Einführung der Null. Dieses erweiterte System wurde um 820 n. Chr. durch al-Khwarizmi, der auch als Namensgeber für den Begriff Algorithmus bekannt ist, in die islamische Welt übertragen.

Das Verständnis für das Nichts unterscheidet sich in der indischen und westlichen Philosophie erheblich. Während die indische Philosophie eine differenzierte Sicht auf das Nichts hat, bereitete das Konzept der westlichen Welt, insbesondere den von den Pythagoreern geprägten Denkern, Schwierigkeiten. Der Mönch Gerbert von Aurillac stieß um 950 n. Chr. auf erheblichen Widerstand, als er versuchte, die Null in Europa einzuführen. Laut pythagoreischer Lehre besteht eine Gleichheit zwischen Zahlen und Formen, doch welcher Form entspricht die Null? Ein Würfel mit der Seitenlänge Null wäre formlos, daher erschien die Idee der Null für die Pythagoreer als etwas, das ihr Weltbild in Frage stellen könnte. Gerberts Versuche, das Konzept der Null zu etablieren, scheiterten letztlich.

Das Konzept der Null war letztlich allerdings auch in der westlichen Welt unaufhaltsam. Seine Verbreitung nahm ihren Anfang entlang der arabischen Handelsrouten und erhielt wichtige Impulse durch Wissenszentren wie die Bibliothek von Córdoba in Spanien. Im Hochmittelalter übersetzten Gelehrte arabische Manuskripte ins Lateinische und machten damit europäischen Mathematikern und Wissenschaftlern dieses revolutionäre Wissen zugänglich.

In Italien fand die Null aus pragmatischen Gründen Anklang. Leonardo von Pisa, besser bekannt als Fibonacci (1170 - 1240 n. Chr.), war der Sohn eines Händlers, der enge Geschäftsbeziehungen zu arabischen Regionen pflegte. Leonardo erkannte die überlegenen Eigenschaften des arabischen Zahlensystems und setzte sich vehement für dessen Einführung ein. Ein Wendepunkt in der europäischen Geschichte der Null war die Veröffentlichung von Leonardos Werk Liber Abaci im Jahr 1202. Darin präsentierte er das dezimale Zahlensystem und unterstrich seine Vorteile gegenüber dem Null-freien römischen System. In den nachfolgenden Jahrhunderten fand die Null immer mehr Anwendung—in der Mathematik, der Buchhaltung und schließlich auch in den Wissenschaften.

Es ist beeindruckend, wie viel Zeit verstrich, bis dieses innovative Konzept sich gegen veraltete Ansichten durchsetzen konnte. Obwohl etwa Zenon von Elea (durch sein Paradox von Achilles und der Schildkröte) und die Atomisten schon früh kritisch gegenüber den Pythagoreern waren, prägte die Aristotelische Weltanschauung fast 2000 Jahre das westliche Denken. Aristoteles hielt sich in diesem Punkt an die Schule des Pythagoras. Denn die Null war weit mehr als eine mathematische Idee. Sie konfrontierte Philosophen und Theologen mit neuen Fragestellungen und stieß anfänglich im christlichen Europa auf erheblichen Widerstand, da sie als Symbol für das Nichts betrachtet wurde—ein Konzept, das dem Schöpfungsglauben entgegenstand. Doch letztlich überwogen die praktischen Vorteile des dezimalen Systems, und die Null setzte sich durch.

Diese Kurzgeschichte zeigt, dass die Evolution von Sprachen, Symbolen, Schrift und Zahlensystemen in einem globalen Kontext stattfindet. Kultureller Austausch war und ist entscheidend für Fortschritt. Ein neuer Blickwinkel auf ein bereits existierendes Konzept kann zu Innovationen führen, die für die ursprünglichen Erfinder*innen oder Entdecker*innen undenkbar gewesen wären.