7.6. Berechenbarkeit

In diesem Abschnitt tauchen wir in die theoretische Informatik ein und widmen uns der Frage was wir überhaupt mit einem Computer berechnen können (Berechenbarkeit). In diesem Zusammenhang folgt unweigerlich die Frage: Welche Mittel benötigen wir um eines der berechenbaren Probleme zu berechnen (Turing-Vollständigkeit)? Außerdem gehen wir der Frage nach, was die Essenz der Computer ist (universelle Turingmaschine), wenn sie doch in Form von Smartwatches und Rechenzentren eine sehr unterschiedliche Gestalt annehmen. Was macht sie dann zu Computern?

Beginnen wir mit einer kurzen Untersuchung von Hard- und Software, d.h., der Bauteile des Computers und der Programmcodes. Stellen Sie sich vor Sie haben einen Addierer als Bauteil. Er steht Ihnen also als Hardware zur Verfügung. Nehmen wir weiter an, dass der Befehl ladd(a,b) diesen realisiert, d.h., die beiden Binärzahlen a und b durch ein Bauteil addiert. Dazu benötigen Sie selbstverständlich eine Kontrolleinheit, welche den Befehl ladd(a,b) so interpretiert, dass sie den Addierer mit den Zahlen a und b füttert und dann aktiviert. Aber gehen wir einmal davon aus, all das hätten zur Verfügung. Wir haben schließlich gesehen, wie dies durch eine Komposition aus Gattern (siehe Manipulation) möglich ist.

Um zwei Zahlen a, b zu multiplizieren könnten wir aus mehreren Addierern einen Multiplizierer bauen. Wir können demnach durch Komposition von bereits existierenden Bauteilen, ein neues Bauteil mit einer neuen Funktion konstruieren. Doch genauso gut können wir durch Programmcode den Addierer mehrfach aufrufen und erhalten so das gleiche Endergebnis. 3 * 5 ist schließlich dasselbe wie 3 + 3 + 3 + 3 + 3.

Show code cell source Hide code cell source

# Transformation einer Zahl in Decimaldarstellung zu ihrer Binärdarstellung
def to_binary(number):
    binary_number = []
    while number != 0:
        r = number % 2
        number = number // 2
        binary_number = [r] + binary_number
    return binary_number

# Transformation einer Zahl in Binärdarstellung zu ihrer Decimaldarstellung
def to_decimal(binary_number):
    decimal_number = 0
    i = len(binary_number)-1
    for bit in binary_number:
        decimal_number += bit * 2**i
        i += -1
    return decimal_number
# Zahl in Binärdarstellung 111 0100 1111 wird umgewandelt

def ladd(a,b): # Wir nehmen an diese Funktion wird durch Bauteile/Hardware umgesetzt
    return to_binary(to_decimal(a) + to_decimal(b))

def mul(a, b):  # Wir nehmen an diese Funktion durch Code/Software umgesetzt
    result = [0 for i in range(len(a))]
    for _ in range(to_decimal(b)): # Python versteht unser Binärsystem nicht
        result = ladd(result,a)
    return result

print(f'{[0,0,1,1]} * {[1,0,0,1]} = {mul([0,0,1,1], [1,0,0,1])}')
print(f'{to_decimal([0,0,1,1])} * {to_decimal([1,0,0,1])} = {to_decimal(mul([0,0,1,1], [1,0,0,1]))}')

[0, 0, 1, 1] * [1, 0, 0, 1] = [1, 1, 0, 1, 1]
3 * 9 = 27

Halten wir also fest: Wir können einen Multiplizierer als Bauteil konstruieren, z.B. indem wir mehrere Addierer hintereinander schalten, oder wir schreiben Programmcode der die Multiplikation durch das mehrfache Aufrufen des Addierers realisiert. Offensichtlich gibt es eine gewisse Ähnlichkeit zwischen Hardware und Software. Wo liegt aber der Unterschied?

Interessiert uns nur das Ergebnis, so ist es egal welche der beiden Methoden wir verwenden. Im Endeffekt sparen wir uns bei der zweiten Berechnung ein Bauteil. In der Praxis spielt es allerdings eine entscheidende Rolle wie lange die Berechnung dauert. Ein Multiplizierer, der als Bauteil vorliegt, wird seine Arbeit deutlich schneller verrichten als die Aufsummierung der Ergebnisse des Addierers vollzogen wird. Werden bestimmte Berechnungen sehr häufig benötigt, so ist es sinnvoll darüber nachzudenken, ob man für diese nicht extra angefertigte Bauteile anbietet.

Die Grafikkarte (GPU) ist ein solches Beispiel. Theoretisch kann die CPU all das berechnen, was die Grafikkarte berechnen kann. Allerdings ist die Grafikkarte darauf optimiert eine bestimmte Operation auf eine Vielzahl an Daten parallel anzuwenden (Single Instruction Multiple Data). Moderne CPUs können das mittlerweile auch, allerdings ist deren Parallelität geringer, d.h., sie besitzen weniger Prozessorkerne. Auch verwenden viele Grafikkarten eine weniger genaue Darstellung der Fließkommazahlen, da bei der Generierung von Bildern oder Animationen kleine Fehler nicht auffallen. Moderne Grafikkarten werden wegen ihres hohen Datendurchsatzes heute für das maschinelle Lernen eingesetzt. Sie sind deshalb mit speziellen Bauteilen ausgestattet, mit denen sich kleiner Matrizen sehr effizient multiplizieren lassen.

Software steuert die Hardware an. Es besteht hier also eine Art Umweg. Löst ein Bauteil das Problem, so ist es mit sehr großer Wahrscheinlichkeit schneller als bestehende Softwarelösung.

Auf algorithmischer Ebene ähneln sich Hardware und Software sehr. Sie gleichen sich, mit dem feinen Unterschied, dass Software eine bestimmte Hardware benötigt um überhaupt lauffähig zu sein.

7.6.1. Turingmaschinen

Der Unterschied zwischen Hard- und Software ist geringer als wir vielleicht angenommen hatten. Klar ist aber auch: Ein Computer ohne Hardware ist nicht funktionsfähig. Wir können nun eine zentrale Fragen der Informatik stellen. Salopp fragen wir:

„Wie viel“ Hardware braucht es denn?

Oder genauer gefragt:

Welche Eigenschaften muss meine Maschine haben, damit ich all das berechnen kann was berechenbar ist?

Und

Was können wir überhaupt berechnen?

Beide Fragen wollte Alan M. Turing mit seinem Berechnungsmodell, der Turingmaschine, beantworten. In seiner 1937 erschienenen Arbeit ‚On computable numbers, with an application to the Entscheidungsproblem‘ [Turing, 1937, Turing, 1938] hat er die Berechenbarkeitstheorie, und damit die Theorie der Informatik begründet. Turings Intention war es eine mathematisch klar beschreibbare Maschine anzugeben, die allgemein genug ist, um stellvertretend für jeden beliebigen algorithmischen Berechnungsprozess zu stehen. Er verwendete diese abstrakte Maschine um zu beweisen, dass es keinen Algorithmus (keine effektive Prozedur) gibt, der das sog. Entscheidungsproblem löst.

Das Entscheidungsproblem

Das Problem zu entscheiden ob ein beliebiger Ausdurck in der Prädikatenlogik erster Stufe ableitbar ist oder nicht.

Diese abstrakte Maschine, d.h. die Turingmaschine, stelle genau diese effektive Prozedur also einen Algorithmus dar. Turing wollte so den zunächst nur intuitiv gegebenen Begriff der Berechenbarkeit exakt beschreiben. Man kann bis heute sagen, dass ihm dies geglückt ist.

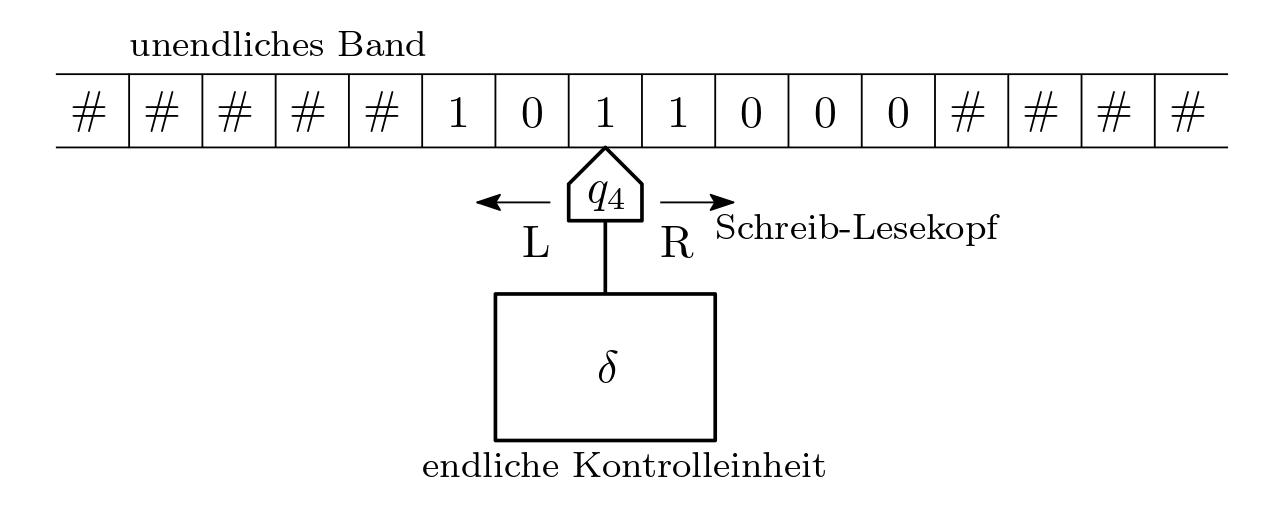
Abb. 7.15 Skizze einer Turingmaschine, die sich gerade in Zustand \(q_4\) befindet.

Die Turingmaschine (TM) besteht aus gerade einmal so viel Hardware, dass sie all das berechnen kann, was allgemein als berechenbar angesehen wird.

Turingmaschine (informell)

Eine Turingmaschine \(T\) besteht aus:

1. Einem unendlich langen Band (unendlichen Speicher) aus Zellen

2. Einem Schreib-/Lesekopf

3. Einer endlichen Übergangstabelle \(\delta\)

4. Einer endlichen Zustandsmenge \(Q\)

5. Einer endlichen Menge and Endzuständen \(F \subseteq Q\)

Der Schreib-/Lesekopf ließt oder schreibt \(0\), \(1\) oder \(\#\) in jeder Zeiteinheit an seine aktuelle Zelle auf dem Band. Dabei steht \(\#\) für eine unbeschriebene Zelle, also das Leerzeichen. Der Kopf kann zudem in einer Zeiteinheit eine Zelle nach links oder rechts fahren oder stehenbleiben. Die Maschine befindet sich in einem von endlich vielen Zuständen.

Gegeben der Zustand \(q\) und das beim Schreib-/Lesekopf stehende Zeichen \(a \in \{0, 1, \#\}\), gibt die Übergangstabelle an:

1. Den Zustand \(p\) den die Maschine einnimmt.

2. Das Zeichen was sie aufs Band schreibt.

3. Ob sich der Schreib-/Lesekopf nach links \(\text{L}\), rechts \(\text{R}\), oder gar nicht \(\text{N}\) bewegt.

Die Turingmaschine befindet sich zu Beginn in einem Startzustand \(q_0\) und die Eingabe befindet sich zu Beginn auf dem Band. Läuft die Turingmaschine irgendwann in einen Endzustand \(q_e \in E\) bleibt sie stehen und das was auf dem Band steht ist das berechnete Ergebnis. Bleibt sie anderweitig stehen, wird das Ergebnis verworfen.

Die Turingmaschine \(T\) berechnet \(T(w)\) für eine Eingabe(wort) \(w\).

Für eine formale Definition verweisen wir auf Schöning [2008] (Seite 73).

Übertragen auf Software, bilden die endliche Übergangstabelle \(\delta\) und die Zustandsmengen \(Q\), \(F\) ein Programm. Diese Tabelle fassen wir auch als Funktion

\[\delta : (Q \setminus F) \times \{0, 1, \# \} \rightarrow Q \times \{0, 1, \#\} \times \{\text{L}, \text{R}, \text{N}\}\]

auf, wobei der Definitionsbereich und der Wertebereich endliche Mengen sind. Aus diesem Grund können wir die Funktion als Tabelle auf ein Blatt Papier schreiben, oder eben als ein Programm in einer Programmiersprache. Befindet sich die Maschine in Zustand \(q\) und steht auf der aktuellen Zelle (dort wo der Schreib-/Lesekopf steht) eine 1, so liefert

\[\delta(q, 1)\]

das was die Maschine zu tun hat, z.B., \((p, 1, \text{N})\), also gehe in Zustand \(p\), schreibe eine 1 und bewege deinen Kopf nicht.

Je nachdem was wir berechnen wollen, müssen wir ein entsprechendes Programm formulieren, d.h. eine Zustandsmenge \(Q\) und eine Übergangstabelle \(\delta\). Da die Turingmaschine nur sehr simple Operationen erlaubt, ist es nicht einfach ein Programm für sie zu schreiben. Schon das Addieren von zwei Zahlen ist eine Herausforderung. Folgende Definition einer Turingmaschine \(Q = \{q_0, q_e\}\), \(F = \{q_e\}\) und \(\delta\):

Aktueller Zustand	Lesen	Nächster Zustand	Schreiben	Bewegung
\(q_0\)	1	\(q_0\)	0	\(\text{R}\)
\(q_0\)	0	\(q_0\)	1	\(\text{R}\)
\(q_0\)	\(\#\)	\(q_e\)	\(\#\)	\(\text{R}\)

berechnet das Komplement einer Binärzahl. Dabei gehen wir davon aus, dass der Schreib-/Lesekopf auf das erste Zeichen der Eingabe zeigt (links). Die Maschine bewegt ihren Kopf einmal von links nach rechts und schreibt eine 0 wenn sie eine 1 ließt und eine 1 wenn sie eine 0 ließt. Sobald sie ein Leerzeichen \(\#\) ließt geht sie in den Endzustand \(q_e\).

Sie können die Turingmaschine auf folgender Webseite ausführen. Kopieren Sie diese Beschreibung der Turingmaschine in das rechte Feld. start entspricht \(q_0\) und done \(q_e\).

input: '10101011'
blank: '#'
start state: start
table:
  done:
  start:
    '0': {write: '1', R: start}
    '1': {write: '0', R: start}
    '#': {write: '#', R: done}

Allgemeine Berechenbarkeit

Ein Problem ist berechenbar, wenn für jenes Problem eine Lösung berechnet werden kann.

Den Schreib-/Lesekopf können wir als CPU und das Band als Speicher interpretieren. Die Endlichkeit von \(Q\), \(F\) und \(\delta\) garantiert, dass unser Algorithmus durch endlich viel Text niedergeschrieben werden kann. Die Turingmaschine geht davon aus, dass ihr unendlich viel Speicher zur Verfügung steht. Das stellt aber kein Problem dar, denn sofern die Maschine stehen bleibt (unser Algorithmus terminiert) kann sie nur endlich viel Zellen auf dem Band abgefahren haben.

Turing-Berechenbarkeit

Ein Problem ist genau dann Turing-berechenbar, wenn eine Turingmaschine existiert, die bei jeder Eingabe hält und die Lösung bei gültiger Eingabe berechnet.

Gültig ist die Eingabe wenn diese das in erwarteter Codierung repräsentiert, was die Maschine verarbeiten soll. Addiert die Maschine zwei Zahlen, dann kann ein korrektes Ergebnis nur erwartet werden, wenn auf dem Band auch zwei Zahlen stehen. Oder in anderen Worten, wenn das Eingabewort \(w\) auch jene zwei Zahlen in der erwarteten Codierung repräsentiert.

Die Probleme die wir mit einer Turingmaschine berechnen können, bilden eine gewisse Problemklasse. Nach der unbeweisbaren Turing-Church-These handelt es sich bei diesen Problemen, um all diejenigen, die im allgemeinen berechenbar sind. Das heißt, für alles was wir allgemein berechnen können, gibt es eine Turingmaschine.

Turing-Church-These (unbeweisbar)

Ein Problem ist genau dann berechenbar, wenn es auch Turing-berechenbar ist.

Nehmen wir an die Turing-Church-These trifft zu, so wissen wir was berechenbar ist und wie viel Hardware es braucht! Wir brauchen soviel Hardware, dass unser Computer all das kann was eine Turingmaschine kann. Alan Turing definierte über diesen Zusammenhang den Begriff der Turing-Vollständigkeit. Eine Rechenmaschine die Turing-vollständig ist, kann all das berechnen was jedwede Turingmaschine berechnen kann. Das gleiche gilt für eine Turing-vollständige Programmiersprache (die natürlich von einem Computer auch ausgeführt werden kann).

Turing-Vollständigkeit

Eine Rechenmaschine (oder Programmiersprache) ist Turing-vollständig genau dann wenn sie all das berechnen kann was jedwede Turingmaschine berechnen kann.

Wenn Sie also verstehen möchten, „wie viel Hardware“ ein Computer braucht, lohnt sich ein Blick hin zur Turingmaschine. Uns ist klar, dass es sich dabei um ein sehr theoretisches Konstrukt handelt. Wir ersparen Ihnen die formale Definition und möchten Sie dennoch bestärken ein intuitives Verständnis über die Turingmaschine während Ihres Studiums aufzubauen.

Die Turingmaschine kommt mit erstaunlich wenig Hardware aus. Pfiffige Bastler*innen können diese Maschine als Heimwerkerprojekt im Keller bauen. Es steht ihnen zwar kein unendliches Band zur Verfügung, doch falls ein Algorithmus terminiert, kann der Schreib-/Lesekopf nur eine endliche Distanz fahren und somit ist ein endliches Band ausreichend. Wie lange dies jedoch sein muss ist im Vornhinein unklar.

Abb. 7.16 Eine konkrete Konstruktion einer Turingmaschine, Quelle.

7.6.2. Die universelle Turingmaschine

Bis heute können wir jedes berechenbare Problem durch eine bestimmte Turingmaschine berechnen. Natürlich müssen wir eine Turingmaschine für das jeweilige Problem konstruieren. Ein Computer löst aber nicht nur ein bestimmtes Problem, sondern ist im Stande jedes Problem, was durch eine Turingmaschine gelöst werden kann, zu berechnen.

Ein Computer ist das Pendant zu einer ganz bestimmten Turingmaschine, der universellen Turingmaschine (UTM). Die universelle Turingmaschine \(U\) (Computer) erhält als Eingabe eine Beschreibung einer andere Turingmaschine \(\alpha_T\) (Programmcode) und die Eingabe \(w\) der Turingmaschine \(T\). Sie simuliert \(T\) unter der Eingabe \(w\)

\[U(\alpha_T, w) = T(w).\]

Das heißt, die universelle Turingmaschine \(U\) berechnet das was die Turingmaschine \(T\) berechnen würde, indem Sie diese simuliert. \(\alpha_T\) und \(w\) stehen auf dem Band von \(U\).

Erneut ist zu betonen dass, da eine Turingmaschine \(T\) durch \(\delta\), \(Q\) und \(F\) vollständig beschrieben ist und all diese Mengen endlich sind, sichergestellt ist dass auch \(\alpha_T\) endlich ist. Der Repräsentant von \(\alpha_T\) muss ein Binärcode sein, sodass wir ihn auf das Band von \(U\) schreiben können. Wie \(U\) genau aussieht werden wir uns nicht ansehen. Sie ahnen vermutlich, dass die Übergangstabelle von \(U\) sehr groß ist.

Universelle Turingmaschine (informell)

Eine universelle Turingmaschine \(U\) ist eine Turingmaschine, die eine beliebige Turingmaschine \(T\) auf beliebiger Eingabe \(w\) simuliert.

7.6.3. Das Halteproblem

Das Halteproblem ist eines der bekanntesten Probleme der Informatik, da es wesentliche Implikationen über die Mächtigkeit von Computern offenlegt. Wir würden uns als Programmierer*innen wünschen, dass es ein Programm gäbe, welches uns für ein anderes beliebiges Programm, mit einer bestimmten Eingabe, verrät, ob dieses auch halten wird oder ob wir in einer Endlosschleife laufen. Gäbe es ein solches Programm könnten sie es verwenden um sicherzustellen, dass sie niemals eine Endlosschleife programmieren.

Das Halteproblem

Gegeben sei eine beliebige Beschreibung \(\alpha_T\) einer Turingmaschine \(T\) und einer beliebigen Eingabe \(w\), so verlangt das Halteproblem, nach der Antwort der Frage ob \(T(w)\) hält oder nicht.

Leider hat sich herausgestellt, dass das Halteproblem nicht berechenbar ist. Der Beweis ist sehr elegant und gut verständlich. Der Trick besteht darin eine Turingmaschine zu konstruieren, die eine andere Turingmaschine entgegennimmt und genau dann hält, wenn die andere Maschine nicht hält und ansonsten nicht hält. Wäre das Halteproblem lösbar, müsste es eine solche Maschine geben. Was passiert aber wenn wir diese Maschine nun mit einer Beschreibung von sich selbst füttern? Es entsteht ein Paradoxon und deshalb kann es eine solche Maschine nicht geben. Einen Beweis finden sie z.B. in Schöning [2008] (Seite 119).

Unberechenbarkeit des Halteproblems

Das Halteproblem ist nicht berechenbar.

Wir können natürlich \(T(w)\) ausführen und einfach abwarten ob die Turingmaschine \(T\) mit der Eingabe \(w\) hält oder nicht. Wenn sie aber nicht hält, können wir das niemals feststellen—wir müssten unendlich lange warten.

Das bedeutet: Es wird niemals einen Algorithmus geben (geschrieben in einer Turing-vollständigen Sprache), welcher für beliebige Programme prüfen kann ob diese auch terminieren. Das bedeutet jedoch nicht, dass wir dies nicht im Einzelfall selbst prüfen können oder das es Programme gibt, die für viele Programme prüfen können ob diese terminieren. Es gibt also Hoffnung.

7.6.4. Zusammenfassung

Weshalb reiten wir so auf diesen theoretischen Konzepten herum? Was kümmern uns imaginäre Turingmaschinen? Diese Maschinen können zwar all das berechnen was ein Computer berechnet, funktionieren aber doch ganz anders. Insbesondere sind sie extrem langsam.

Computer und Programmiersprachen sind Werkzeuge, um unsere Konzepte, welche durch Computational Thinking entstehen, zu realisieren. Was aber können wir überhaupt mit diesen Werkzeugen realisieren? Die Antwort folgt aus der eben besprochenen Turingmaschine, denn jeder Ihnen bekannte Computer und jede Programmiersprache welche Sie erlernen werden ist Turing-vollständig!

Jeder Computer kann genau das berechnen, was Turing-berechenbar ist. Selbstverständlich arbeiten Computer mit vollkommen anderen Bauteilen, was sie viel effizienter macht. Im wesentlichen sind sie dennoch nichts anderes als effiziente Turingmaschinen. John von Neumann’s Prinzip des speicherprogrammierten Computers basiert auf Alan Turing’s Turingmaschine.

Für alle gängigen Programmiersprachen gilt, dass Sie mit ihnen Algorithmen formulieren können, die eine Lösung berechnen, welche auch von einer Turingmaschine berechnet werden kann!

Exercise 7.13 (Kompilieren und Interpretieren)

Angenommen Sie haben zwei Turing-vollständige Programmiersprachen \(L_1\) und \(L_2\). Ihr Computer versteht jedoch nur die Sprache \(L_1\). Können Sie ein Programm \(\alpha_{T_2}\), geschrieben in der Sprache \(L_2\), ausführen und wenn ja wie?

Solution to Exercise 7.13 (Kompilieren und Interpretieren)

Ja das ist möglich! Zur Übung verwenden wir für unsere Lösung die Notation der Beschreibung \(\alpha_T\) einer Turingmaschine \(T\) und die Programmausführung \(T(w)\) für eine Eingabe \(w\).

1. Kompilieren: Da beide Sprachen Turing-vollständig sind, können Sie einen Übersetzer/Compiler \(\alpha_{T_C}\) in der Sprache \(L_1\) schreiben, sodass für jedes beliebige Programm \(\alpha_{T_2} \in L_2\) gilt: \(T_C(\alpha_{T_1}) = \alpha_{T_2}\) mit \(T_1(w) = T_2(w)\) für jede beliebige Eingabe \(w\). Diesen Vorgang nennen wir kompilieren.

2. Interpretieren: Sie können auch einen Interpreter \(\alpha_{T_I}\) in der Sprache \(L_1\) schreiben. Dieser gleicht einer universellen Turingmaschine und simuliert Programme \(\alpha_{T_2}\), welche in der Sprache \(L_2\) geschrieben sind. Das heißt \(T_I(\alpha_{T_2}, w) = T_2(w)\) für eine beliebige Eingabe \(w\).

Gehen wir nun zurück zur Frage nach dem Unterschied zwischen Hard-/ und Software. Der wesentlichen Unterschied zwischen dem Computer (Hardware) und einem Programm (Software) ist die Art und Weise wie die Turing-Vollständigkeit realisiert wird—durch elektrische Bauteile oder eine Programmiersprache. Programme als auch Computer sind Turingmaschinen und da der Computer Programme also andere Turingmaschinen simuliert, ist er eine universelle Turingmaschine.

Computer sind universelle Turingmaschinen

Ein handelsüblicher Computer ist eine universelle Turingmaschine.

Sobald ein Computer Turing-vollständig ist, sind alle weiteren Bauteile ein Bonus. In der Theorie ist die universelle Turingmaschine ebenso „schnell“ wie ein moderner Computer. In der Praxis wäre sie allerdings unfassbar langsam. In der Theorie ist auch jeder Prozessor „gleich schnell“. In der Praxis ist das natürlich nicht der Fall. Die Turingmaschine hilft uns dabei die Begriffe „schnell“, „schneller“, „langsamer“ und „gleich schnell“ formal zu definieren.

Zusätzliche oder effizientere Hardware dient im wesentlichen der Beschleunigung bestimmter Berechnungen. Ein Beispiel, was wir oben bereits besprochen haben ist die Grafikkarte (GPU). In der Theorie ist sie „genauso schnell“ wie eine CPU. Dennoch hat jeder gängige Heim-Computer eine Grafikkarte, da diese für Berechnungen im 3D-Grafikbereich optimiert ist.

Wichtig ist festzuhalten, dass sich Hardware und Software auf konzeptioneller Ebene gleichen. Hardware ist die Manifestation von Software und Software ist die Manifestation des Computational Thinkings und so entspringt auch Hardware aus dem Computational Thinking!

7.6.5. Begründer der Informatik

Man muss sich vor Augen halten, dass Alan Turing bereits 1937 die Grundlagen für alle modernen Computer und Programmiersprachen dieser Welt gelegt hat. Und wir sollten auch erwähnen, dass es ihm die Gesellschaft in jener Zeit nicht gerade gedankt hat. Turing wurde 1952 wegen homosexueller Handlungen strafrechtlich verfolgt. Als Alternative zum Gefängnis akzeptierte er eine Hormonbehandlung mit DES, ein Verfahren, das allgemein als chemische Kastration bezeichnet wird. Turing starb am 7. Juni 1954, 16 Tage vor seinem 42. Geburtstag, an einer Zyankali-Vergiftung. Eine Untersuchung stellte seinen Tod als Selbstmord fest, aber es wurde angemerkt, dass die bekannten Beweise auch mit einer versehentlichen Vergiftung übereinstimmen könnten.

Abb. 7.17 Alan M. Turing, Quelle

Königin Elisabeth II. gewährte 2013 eine posthume Begnadigung. Der Begriff Alan Turing-Gesetz wird heute informell verwendet, um sich auf ein Gesetz aus dem Jahr 2017 im Vereinigten Königreich zu beziehen, das Männer rückwirkend begnadigte, die aufgrund historischer Gesetze, die homosexuelle Handlungen unter Strafe stellten, verwarnt oder verurteilt wurden.

Folgende Errungenschaften kann man Alan Turing zuschreiben:

1. Turingmaschine: Turing formulierte das Konzept der Turingmaschine, ein einfaches theoretisches Gerät, das als Grundlage für den Bereich der theoretischen Informatik dient [Turing, 1937].

2. Entscheidungsproblem: Turing zeigte, dass es für bestimmte Klassen von mathematischen Problemen keine allgemeine algorithmische Lösung gibt, was Hilberts Entscheidungsproblem beantwortete [Turing, 1937].

3. Zweiter Weltkrieg und Kryptoanalyse: Turing spielte eine zentrale Rolle bei der Entschlüsselung des deutschen Enigma-Codes, was den Alliierten half, den Zweiten Weltkrieg zu gewinnen.

4. Automatischer Rechenplan: Turing arbeitete an der Konzeption und Teilkonstruktion des Automatic Computing Engine (ACE), eines der ersten Konzepte für einen universellen Computer.

5. Künstliche Intelligenz: Mit dem Turing-Test schuf er ein Kriterium, um die Fähigkeit einer Maschine zur Ausführung von „intelligentem“ oder „menschlichem“ Verhalten zu bewerten.

6. Morphogenese: Turing veröffentlichte Arbeiten zur biologischen Morphogenese, insbesondere zur Erklärung der Entstehung von Mustern in der Natur, wie Streifen und Flecken bei Tieren [Turing, 1952].

7. Programmiersprachen und Algorithmen: Obwohl er keine spezielle Programmiersprache entwickelte, beeinflussten seine Theorien zur Berechenbarkeit und seine Arbeit an den ersten Computern die Entwicklung der ersten Programmiersprachen und Algorithmen.

8. Homosexualität und gesellschaftliche Auswirkungen: Trotz seiner Verurteilung und chemischen Kastration aufgrund seiner Homosexualität hat Turing posthum als LGBT-Ikone und als Beispiel für die schädlichen Auswirkungen von Diskriminierung Anerkennung gefunden.

9. Posthume Ehrungen: Turing wurde 2013 von Königin Elisabeth II. posthum begnadigt, und sein Einfluss wird durch zahlreiche Ehrungen, darunter Filme, Bücher und Namensgebungen (z.B. die Turing-Auszeichnung) anerkannt.