7.4. Manipulation#
Eingabegeräte transformieren Information, wie etwa einen Tastendruck oder die Aufnahmen einer Videokamera, in elektrische Signale. Sie realisieren eine bestimmte Interpretation \(I\). Die Tastatur interpretiert unseren Tastendruck einer bestimmten Taste und gibt ihre Bedeutung an die anderen Bauteile des Computers weiter. Die elektrischen Signale (Strom aus und Strom an) gelangen über mikroskopisch kleine Leitungen in sogenannte Schaltkreise. Dort werden die Signale, d. h. die Bits und Byte weiterverarbeiten.
Logikgatter oder kurz Gatter sind konzeptionelle Anordnungen von elektrischen Schaltungen, welche boolsche Operationen durchführen.
Gatter und Bauteile
Gatter beschreiben die Funktionsweise. Elektrische Schaltkreise und Transistoren sind eine mögliche Realisierung. Gatter sind konzeptionelle Bauteile wohingegen elektrische Schaltkreise, Transistoren, Leitungen und Flip-Flops (später mehr dazu) physikalische Bauteile sind.
Ein oder zwei Signale gelangen in ein Gatter und, je nachdem um welches Gatter es sich handelt, wird ein bestimmtes Ausgabesignal ausgegeben. Das Ausgabesignal hängt von den ein oder zwei Eingabesignalen und dessen Typ des Gatters ab. Jedes Gatter realisiert eine (mathematische) Funktion.
7.4.1. Basis Gatter#
Das einfachste Not-Gatter nimmt als Eingabe ein Signal und gibt dessen Negation davon aus. Aus 0 wird 1 und aus 1 wird 0.
def lnot(bit):
return int(not bit)
print(lnot(0))
print(lnot(1))
1
0
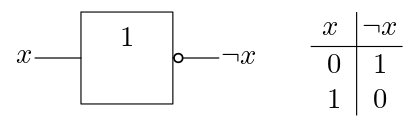
Abb. 7.7 Das Symbol für das Not-Gatter (links) und seine Ein- und Ausgabewerte (rechts).#
Ein weiteres sehr einfaches Gatter ist das sogenannte AND-Gatter. Es kombiniert zwei Signale und gibt genau dann 1 aus, wenn beide Eingabesignale gleich 1 sind.
def land(in1, in2):
return in1 and in2
print(land(0,0))
print(land(0,1))
print(land(1,0))
print(land(1,1))
0
0
0
1
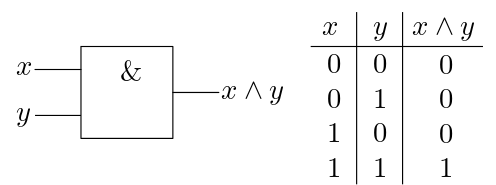
Abb. 7.8 Das Symbol für das AND-Gatter (links) und seine Ein- und Ausgabewerte (rechts).#
Zu guter Letzt fehlt noch das OR-Gatter. Es kombiniert zwei Signale und gibt 1 aus genau dann wenn eines oder beide der Eingabesignale gleich 1 sind.
def lor(in1, in2):
return in1 or in2
print(lor(0,0))
print(lor(0,1))
print(lor(1,0))
print(lor(1,1))
0
1
1
1
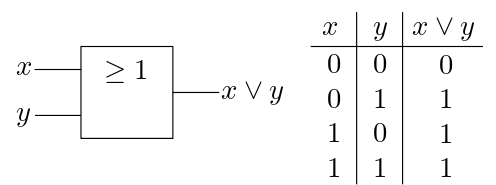
Abb. 7.9 Das Symbol für das OR-Gatter (links) und seine Ein- und Ausgabewerte (rechts).#
Exercise 7.10 (OR-Gatter)
Das Symbol für das OR-Gatter enthält das größer gleich Zeichen \(\geq\).
Was könnte das für einen Grund haben?
Schreiben Sie eine Python Funktion lor(in1, in2) die sich diesen Grund zunutze macht.
Tipp: Denken Sie an die Addition.
Solution to Exercise 7.10 (OR-Gatter)
Der Grund dafür ist, dass das Gatter genau dann 1 ist wenn
gilt.
def lor(in1, in2):
return int(in1 + in2 >= 1)
print(lor(0,0))
print(lor(0,1))
print(lor(1,0))
print(lor(1,1))
Jedes Gatter können wir auch als Interpretation \(I\) beschreiben. Zum Beispiel wäre die Interpretation des AND-Gatters durch folgende Mengen gegeben:
Bedeutung \(B_{\text{AND}} = \left\{0, 1\right\}\)
Repräsentation \(R_{\text{AND}} = \left\{ 00, 01, 10, 11 \right\}\)
Interpretation \(I_{\text{AND}} = \left\{ (00, 0), (01, 0), (10, 0), (11, 1) \right\}\).
Nun gut, diese Operationen scheinen lächerlich einfach zu sein, aber kombinieren wir mehrere Gatter können wir mehr und mehr komplexe Operationen durchführen. Im Endeffekt basieren alle Berechnungen des Computers auf diesen sehr primitiven Gattern/Operationen. Die Logikgatter implementieren die sog. boolsche Algebra.
Obwohl sehr viele kleine Operationen notwendig sind, lassen sich diese Operationen sehr schnell durchführen. Signale breiten sich mit annähernd Lichtgeschwindigkeit aus und so sind gigantische Mengen an primitiven Operationen in sehr kurzer Zeit durchführbar. Je kleiner die Chips, desto kleiner ist die Distanz, welche die Signale überwinden müssen und desto schneller ist der Computer.
7.4.2. Komplement#
In Abschnitt Ganze Zahlen haben wir besprochen wie diese durch das zweier Komplement repräsentiert werden. Um aus eine Binärzahl \(k = b_{n-1}\ldots b_0\) ihr Negativ zu bilden, also \(-k\), bilden wir das Komplement und addieren eins:
Wie würden wir das Komplement \(\overline{b_{n-1}\ldots b_0}\) mit Gattern realisieren? Jedes Signal \(b_i\) muss durch ein Not-Gatter negiert werden. Somit könnten wir die Signale der Binärzahl durch \(n\) Not-Gatter hindurch schicken und würden ihr Komplement erhalten:
def complement(b3, b2, b1, b0):
return lnot(b3), lnot(b2), lnot(b1), lnot(b0)
print(complement(0,0,0,0))
print(complement(1,0,1,1))
(1, 1, 1, 1)
(0, 1, 0, 0)
7.4.3. Addierer#
Betrachten Sie einmal land und lor.
Welche mathematische Funktion realisieren diese einfachen Gatter?
Nun ja, wenn wir die beiden Eingabesignale als Zahlen interpretieren, dann ist land gleich dem Minimum min und lor gleich dem max der beiden Signale:
def lor(in1, in2):
return max(in1, in2)
def land(in1, in2):
return min(in1, in2)
print(lor(0,0))
print(lor(0,1))
print(lor(1,0))
print(lor(1,1))
print(land(0,0))
print(land(0,1))
print(land(1,0))
print(land(1,1))
0
1
1
1
0
0
0
1
Diese Operation ist sehr simpel. Dennoch berechnen wir mit nur einem Gatter bereits etwas.
Im folgenden wollen wir Ihnen durch den Bau eines \(n\)-Bit Addierers zeigen, wie wir durch Komposition aus einfachen Berechnungen/Bauteilen komplexe Berechnungen/Bauteilen realisieren können.
7.4.3.1. 1-Bit-Addierer#
Bauen wir aus den gegebenen Gattern einen Addierer der zwei Zahlen \(a, b \in \{0,1\}\) addiert. Der Addierer erhält zwei Eingabesignale \(a, b\) und gibt zwei Signale \(c = c_0, c_1\) aus. Sei \(c = c_1c_0\) das Ergebnis der Addition. Lassen Sie uns alle Möglichkeiten notieren:
Wir erhalten \(c_1 = 1\), d.h. einen Übertrag von \(1\) genau dann wenn \(a\) und \(b\) gleich \(1\) sind. Hingegen ist \(c_0\) genau dann \(1\) wenn entweder \(a\) oder \(b\), nicht aber beide, gleich \(1\) sind. Daraus ergeben sich folgende boolsche Operationen:
Wir haben diese Operationen als Python Funktion implementiert.
def ladd(in1, in0):
# c1 = a and b
out1 = land(in1,in0)
# c0 = (not c1) and (a or b)
out0 = land(lnot(out1), lor(in0, in1))
#return c1c2
return [out1, out0]
ladd(1,1)
[1, 0]
Als Gatter-Bauplan sieht das ganze wie folgt aus.
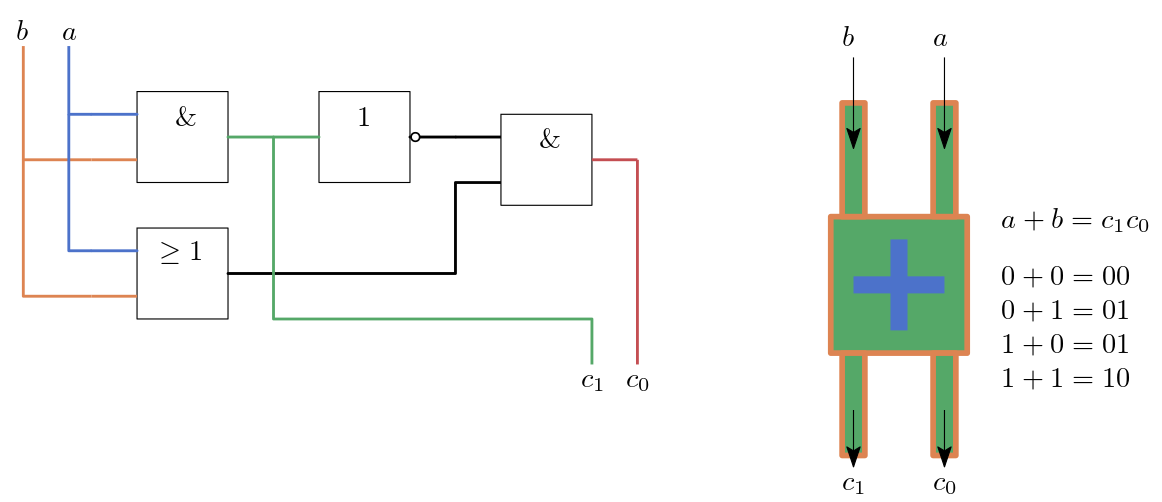
Abb. 7.10 Skizze eines 1-Bit-Addierers. Der Zusammenschluss der Gatter (links) und das Symbol für unseren Addierer (rechts).#
7.4.3.2. Erweiterter 1-Bit-Addierer#
Durch vier Gatter lassen sich also zwei 1-Bit Zahlen addieren. Was passiert wenn wir die Anzahl der Bits erhöhen? Immerhin ist das Addieren von 1-Bit Zahlen doch sehr einschränkend. Addieren wir größere Zahlen, so stellen wir fest, dass sich diese Operation auf den 1-Bit-Addierer zurückführen lässt. Wenn Sie, zum Beispiel,
berechnen, so betrachten Sie in jedem Berechnungsschritt lediglich 3 Bits:
das Bit an der \(i\)-ten Stelle der ersten Zahl
das Bit an der \(i\)-ten Stelle der zweiten Zahl
und den Übertrag der letzten (\(i-1\)-ten) 1-Bit-Addition!
So lautet die erste Rechnung \(1+1+0 = 0\) und der Übertrag ist gleich \(1\). Die zweite Rechnung lautet \(0+0+1 = 1\) und der Übertrag ist gleich \(0\). Die dritte lautet \(0+1+0 = 1\) und der Übertrag ist gleich \(0\). Die vierte und letzte lautet \(1+1+0 = 0\) und der Übertrag ist \(1\). Daraus ergibt sich:
binär, was
im Dezimalsystem ergibt.
Wir addieren also je drei 1-Bit Zahlen! Unser Addierer von oben addiert jedoch nur zwei 1-Bit Zahlen. Lassen Sie uns also einen 1-Bit-Addierer der drei Zahlen addieren kann konstruieren. Dieser dient dann der Konstruktion des \(n\)-Bit-Addierers. Wir benötigen einen 1-Bit-Addierer mit drei Eingabesignale \(u, a, b\) und weiterhin zwei Ausgabesignalen \(c_0, c_1\), jedoch interpretieren wir diesmal \(u\) als Übertrag für den nächsten Addierer!
Lassen Sie uns erneut alle Möglichkeiten notieren:
Betrachten Sie nun \(c_0\). Fragen wir uns: wann wird \(c_0\) gleich \(1\)? \(c_0\) wird genau dann \(1\), wenn genau eines der drei Eingabesignale \(1\) ist, d.h., wenn
oder alle drei Eingabesignale gleich \(1\) sind, d.h., wenn
Zusammengefasst ergibt sich
Das scheint sehr ausschweifend, jedoch nur weil wir auf sehr primitive Operationen zurückgreifen können. Wie sieht es mit \(c_1\), also unserem Übertrag aus? \(a_1\) ist genau dann \(1\) wenn mehr als 1-Bit der Eingabe gleich \(1\) ist, d.h.
Kennen wir \(c_1\) dann können wir \(c_0\) etwas kürzer schreiben. Denn anstatt zu sagen es muss genau eines der drei Eingabesignale \(1\) sein, können wir auch sagen: es gibt keinen Übertrag (\(c_1 = 0\)) und irgendein Eingabesignal ist \(1\). Aus
wird
und wir erhalten insgesamt:
def ladd(in2, in1, in0):
# u and a
and01 = land(in1,in0)
# a and b
and12 = land(in1,in2)
# u and b
and02 = land(in0,in2)
# u or a or b
or_all = lor(lor(in0, in1), in2)
# u and b1 and b
and_all = land(and01, in2)
# (u and b1) or (b1 and b) or (u and b)
out1 = lor(lor(and01, and12), and02)
# (u and a and b) or ((not c1) and (u or a or b))
out0 = lor(and_all, land(lnot(out1), or_all))
return [out1, out0]
print(ladd(0,0,0))
print(ladd(0,0,1))
print(ladd(0,1,0))
print(ladd(0,1,1))
print(ladd(1,0,0))
print(ladd(1,0,1))
print(ladd(1,1,0))
print(ladd(1,1,1))
[0, 0]
[0, 1]
[0, 1]
[1, 0]
[0, 1]
[1, 0]
[1, 0]
[1, 1]
7.4.3.3. \(n\)-Bit-Addierer#
Für einen \(n\)-Bit-Addierer brauchen wir \(n\) hintereinander geschaltene 1-Bit-Addierer, welche alle (bis auf den ersten) drei Signale aufnehmen. Wie oben erwähnt addiert der \(i\)-te 1-Bit-Addierer das \(i\)-te Bit der beiden Eingabezahlen und den Übertrag des \((i-1)\)-ten 1-Bit-Addierers. Für den ersten Addierer ist der Übertrag \(u\) gleich \(0\).
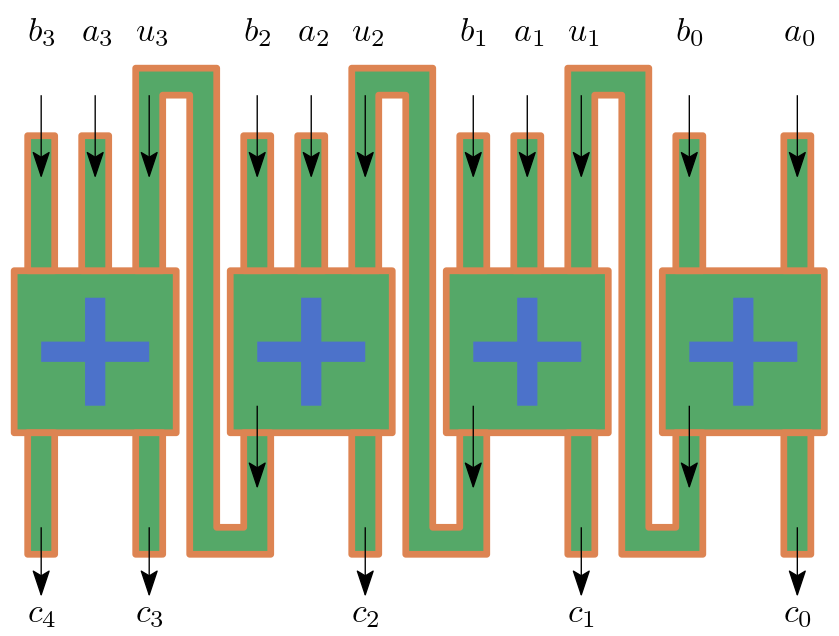
Abb. 7.11 Skizze eines 4-Bit-Addierers, der \(a + b = c\) berechnet. Dabei sind \(a, b\) 4-Bit Zahlen und \(c\) eine 5-Bit Zahl: \(c_4c_3c_2c_1c_0 = a_3a_2a_1a_0 + b_3b_2b_1b_0\)#
Hier sehen Sie den Python Code eines \(4\)-Bit-Addierers (wir lesen die Bits von rechts nach links, d.h. das Bit an der Stelle 0 in der liste ist das höchste Bit!):
def ladd4(a, b):
# a[3] und b[3] sind die erste Eingabesignale (niedrigsten Bits)
u1, c0 = ladd(a[3], b[3], 0)
u2, c1 = ladd(a[2], b[2], u1)
u3, c2 = ladd(a[1], b[1], u2)
c4, c3 = ladd(a[0], b[0], u3)
return [c4, c3, c2, c1, c0]
ladd4([0,0,1,1], [1,0,0,1])
[0, 1, 1, 0, 0]
Hängt man nun Addierer aneinander so kann man einen Multiplizierer und andere Recheneinheiten wie Fließkommaddierer und mehr bauen.
Exercise 7.11 (\(n\)-Bit-Addierer)
Definieren Sie eine Python-Funktion laddn(a, b), die unter Verwendung von ladd(in1, in2, in3) Bits variabler länge addiert.
Gehen Sie davon aus, dass die Listen a und b die gleiche Länge haben.
Hinweis: Studieren Sie den obigen Code, d.h. ladd4. Was wiederholt sich immer wieder und lässt sich somit automatisieren?
Solution to Exercise 7.11 (\(n\)-Bit-Addierer)
def laddn(a, b):
u = 0
n = len(a)
result = []
for i in range(n):
u, c = ladd(a[n-1-i], b[n-1-i], u)
result = [c] + result
result = [u] + result
return result
laddn([1,1,1,1], [1,0,0,1])
Modellierung der Gatter und Addierer
Unser Python Code modelliert den Addierer als Gatterzusammenschluss.
Natürlich können wir in Python deutlich einfacher zwei Zahlen addieren.
Es gibt auch noch andere Gatter als AND, NOT und OR z.B. NAND, XOR oder NOR, aber all diese Gatter lassen sich durch die drei fundamentalen Gatter ausdrücken.
Anzahl, Größe und Geschwindigkeit
Gatter beschreiben die Funktionsweise, realisiert durch Transistoren, sind unvorstellbar klein und können unvorstellbar oft angesteuert werden. Transistoren sind dünner als wenige Nanometer (etwa 4000 mal dünner als ein Haar) und lassen sich hunderte Milliarden Mal in der Sekunde ansteuern. Zum Beispiel befinden sich auf dem Intel i7 4770K Prozessor ca. 1.4 Milliarden Transistoren auf einer Fläche von 177 Quadratmillimeter.

