8.2. Strukturwissenschaften#

8.2.1. Nachrichtentechnik#

1948 griff Claude E. Shannon den physikalischen Begriff der Entropie auf und übetrug ihn auf die Nachrichtenübertragung. Sein Modell prägte die Informatik über viele Jahre und ist heute noch relevant. Es ist äußerst wichtig zu verstehen, dass es Shannon um die Informationsübertragung ging. Sie ist für sein Modell von zentraler Bedeutung.

Frequently the messages have meaning; that is, they refer to or are correlated according to some system with certain physical or conceptual entities. These semantic aspects of communication are irrelevant to the engineering problem. The significant aspect is that the actual message is one selected from a set of possible messages. The system must be designed to operate for each possible selection, not just the one which will actually be chosen since this is unknown at the time of design – [Shannon, 1948]

Shannon war sich bewusst, dass zur Information auch Ihre Bedeutung (Semantik) gehört, doch befand er diese für die Informationsübertragung über ein Medium als irrelevant.

Die Übertragung besteht dabei aus mehreren Teilen:

  1. Eine (Informations)-Quelle versendet eine Nachricht.

  2. Diese Nachricht wird durch einen Sender in ein Signal codiert und in einen Kanal eingespeist.

  3. Der Kanal ist das Medium der Übertragung, beispielsweise ein Netzwerkkabel. Bei dieser Übertragung kann es zu einer Störung durch eine Störquelle kommen. Unter Umständen ist das erhaltene Signal gestört.

  4. Ein Empfänger empfängt dieses, möglicherweise gestörte erhaltene Signal, decodiert es und leitet es an das Ziel weiter.

  5. Die decodierte Nachricht kommt bei ihrem Ziel an.

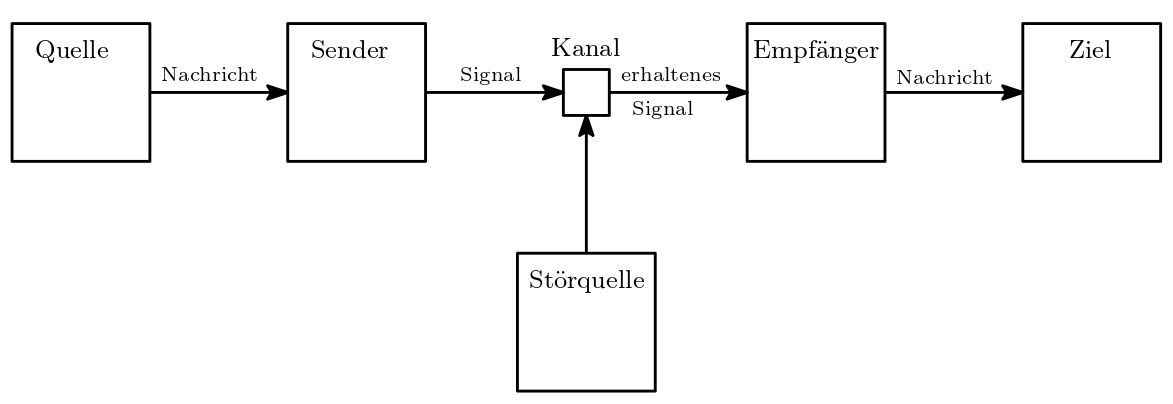
../../_images/shannon-messages.png

Abb. 8.2 Shannon’s Schema der Nachrichtenübertragung bzw. Kommunikation.#

In diesem Modell ist die Nachricht/Symbolfolge/Zeichenfolge eine Information und der Informationsgehalt steigt mit der Anzahl der möglichen Nachrichten.

If the number of [possible] messages […] is finite then this number […] can be regarded as a measure of the information produced when one message [… from the set of possible messages], all choices being equally likely – Claude E. Shannon

8.2.1.1. Information und Sinn#

Betrachten wir die folgenden beiden Zeichenfolgen:

  1. Prüfung bestanden

  2. brüeung Pfnsanedt

Nach Shannon’s Definition enthalten beide Symbolketten/Zeichenfolgen gleich viel Information. Die Anzahl der Bits, welche wir bräuchten um die beiden Nachrichten auf einem Kanal zu übertragen ist dieselbe. Intuitiv würden wir sagen, dass die erste Nachricht mehr Information beinhaltet. Dies liegt daran, dass wir automatisch die Semantik (Bedeutung) einer Zeichenfolge betrachten. Wir verwechseln dabei die Begriffe Information und Sinn. Das heißt beide Nachrichten enthalten gleich viel Information aber die zweite ergibt keinen Sinn.

Shannon’s Definition ist rein syntaktisch, denn Maschinen fehlt (bis heute) die Eigenschaft der semantischen Betrachtung—d.h. der Sinnerschließung oder der semiotischen Interpretation. In der Informatik gibt es deshalb (noch) keine befriedigende Definition des Sinns, welcher der Bedeutung der betrachteten Information gerecht wird. Im Sinne der Informationsverarbeitung bleiben wir bei der syntaktischen Betrachtung. Jedoch sei erneut betont, dass sich die Bedeutung oder der Sinn in Informationssysteme einschleicht, wenn diese Auswirkungen auf das gesellschaftliche Leben haben. Ein System, welches Ihnen automatisch einen Kredit aufgrund Ihrer getätigten Ausgaben verweigert, tut dies Aufgrund des Sinns den die Bank aus den Informationen zieht.

Gehen wir zurück zu unserem Einführungsbeispiel in der U-Bahn. Falls der Wetterbericht Ihnen lediglich mitteilen kann ob es regnet oder nicht, so ist der Informationsgehalt von „es regnet“ gering. Wenn aber der Wetterbericht Ihnen unterschiedliche Arten von Regen oder andere Wetterlagen berichten kann, so trägt eine dieser konkreten Wetterlagen einen großen Informationsgehalt in sich. Ob es draußen 25 Grad oder 25.00001 Grad hat, ist Ihnen höchst wahrscheinlich gleichgültig. Das heißt zwei durchaus sehr unterschiedliche Informationen können den annähernd gleichen Sinn ergeben. Ein Wetterbericht der Ihnen die Temperatur auf fünf Nachkommastellen genau berichtet, liefert nach Shannon’s Definition einen viel höheren Informationsgehalt als ein Dienst, der bei der ersten Nachkommastelle rundet.

8.2.1.2. Entropie (Informatik)#

Einer der Vorzüge der (strukturwissenschaftlichen) Definition ist, dass wir ein Maß für den Informationsgehalt definieren können. Shannon misst den Informationsgehalt einer Nachricht über die Entropie, welche uns in der Physik schon über den Weg gelaufen ist. Die Entropie in der Informatik ist ein Maß für den mittleren Informationsgehalt einer Nachricht.

Betrachten wir eine bestimmte endliche Menge an Zeichen die bei einer Übertragung auftauchen können. Diese Menge bezeichnet man üblicherweise als Alphabet \(\Sigma\). Sei nun \(\sigma \in \Sigma\) ein Zeichen. Wie wahrscheinlich ist es, dass ein Zeichen \(X\) einer Nachricht gleich \(\sigma\) ist, d.h. wie groß ist

\[P(X = \sigma) \stackrel{?}{=} p_\sigma\]

Wenn jedes Zeichen mit gleicher Wahrscheinlichkeit in einer Nachricht auftritt, dann ist

\[P(X = \sigma) = \frac{1}{N},\]

wobei \(N = |\Sigma|\) gleich der Anzahl der Zeichen im Alphabet \(\Sigma\) ist.

Wie viel Information steckt dann in einem Zeichen? Anders gefragt: Wie viel Unsicherheit eliminiert ein Zeichen oder wie viel Ja/Nein Fragen müssten wir stellen um auf das übertragene Zeichen \(\sigma\) zu kommen? Je kleiner \(p_\sigma\), desto mehr Unsicherheit wird eliminiert. Ein Vorschlag wäre der deshalb

\[\frac{1}{p_\sigma}.\]

Allerdings ist dieser Term nicht besonders aussagekräftig. Ist \(p_\sigma\) gleich 1, so wird eine Unsicherheit von 1 eliminiert. Stattdessen verwendet Shannon den Logarithmus:

\[\log_N\left( \frac{1}{p_\sigma} \right).\]

Es gilt:

\[\lim\limits_{p_\sigma \rightarrow 0^{+}}\log_N\left( \frac{1}{p_\sigma} \right) = \infty\]

und

\[\log_N\left( \frac{1}{1} \right) = 0.\]

Zudem ist

\[\lceil \log_N\left( 1/p_\sigma \right) \rceil\]

die Anzahl der Symbole aus \(\Sigma\), die wir benötigen um \(1/p_\sigma\) Elemente einer Menge zu codieren bzw. zu repräsentieren. Siehe hierzu die Aufgabe Sprechen in der Taucherglocke. Jedes Zeichen \(\sigma_i\) kann eine andere Auftrittswahrscheinlichkeit \(p_i\) besitzen. Der Informationsgehalt \(I\), der dann in dem \(i\)-ten Symbol \(\sigma_i\) einer Nachricht steckt, ist durch

\[I(\sigma_i) = \log_2\left( \frac{1}{p_i} \right) = -\log_2(p_i)\]

gegeben.

Entropie (Informatik)

Sei \(X\) eine Zufallsvariable einer gedächtnislosen Quelle über einem endlichen, aus Zeichen bestehenden Alphabet \(\Sigma = \left\{ \sigma_1, \ldots, \sigma_m \right\}\). Sei \(p_i = P(X = \sigma_i)\) die Wahrscheinlichkeit, dass die Zufallsvariable \(X\) das Zeichen \(\sigma_i\) annimmt. Dann ist

\[I(\sigma_i) = \log_m(1/p_i) = - \log_m(p_i)\]

der Informationsgehalt des Zeichens (notwendige Anzahl an Symbolen um \(1 / p_i\) Ereignisse zu unterscheiden).

Die Entropie eines Zeichens ist definiert als der Erwartungswert des Informationsgehalts:

\[H_1 = E[I] = \sum^m_{i=1} p_i I(\sigma_i) = - \sum^m_{i=1} p_i \log_m(p_i).\]

Die Entropie \(H_n\) für Wörter \(w \in \Sigma^n\) der Länge \(n\) ergibt sich durch

\[H_n = - \sum_{w \in \Sigma^n} p_w \log_m(p_w),\]

wobei \(p_w = P(X = w)\) die Wahrscheinlichkeit ist, mit der das Wort \(w\) auftritt.

Die Entropie \(H\) ist der Limes \(n \rightarrow \infty\)

\[H = \lim_{n \rightarrow \infty} \frac{H_n}{n}.\]

Da Computer im Binärsystem arbeiten, ist in unserem Fall \(\Sigma = \mathbb{B} = \{0, 1\}\) und \(m = 2\).

Lassen Sie sich nicht von den mathematischen Symbolen abschrecken. Kurz gesagt: Je größer die Gewissheit, desto kleiner ist der Informationsgehalt. Oder anders ausgedrückt: Je größer die Überraschung, desto größer ist der Informationsgehalt. Information führt zur Beseitigung von Unsicherheit. Je mehr Unsicherheit beseitigt wird, desto größer ist der Informationsgehalt!

Zwischen der Entropie eines Zeichens und den notwendigen Bits einer Nachricht gibt es einen schönen Zusammenhang: Ist ein bestimmtes Alphabet \(\Sigma\) mit all den Auftrittswahrscheinlichkeiten seiner Zeichen gegeben, so benötigen wir im Mittel

\[n \cdot H_1\]

Bits um eine Nachricht bestehend aus \(n\) Zeichen zu übertragen.

Das Konzept der Entropie wird schnell anhand eines Beispiels klar. Nehmen wir den Münzwurf mit einer perfekten Münze. Werfen Sie die Münze einmal, so ist der Informationsgehalt \(H_1 = 1\), denn die Wahrscheinlichkeit für Kopf oder Zahl liegt bei \(0.5\) und daraus ergibt sich:

\[H_1 = 0.5 \cdot \log_2(2) + 0.5 \cdot \log_2(2) = 0.5 + 0.5 = 1\]

Die Informationsquelle ist der Münzwurf, die Nachricht das Ergebnis des Wurfes, und der Empfänger sind wir als Beobachter*innen des Wurfs.

Exercise 8.1 (Entropie)

Welche Entropie \(H\) hat die Nachricht, die von einer Informationsquelle stammt, welche durchgehend \(1\) sendet?

Lassen Sie uns ein weiteres Beispiel betrachten. Stellen Sie sich vor, Sie hätten eine Informationsquelle die fortwährend die Folge \(0,1,0,1,0,1, \ldots\) ausspuckt. Für \(H_1\) ergibt sich \(H_1 = 1\), denn wie beim Münzwurf besteht eine Wahrscheinlichkeit von \(0.5\) ob wir eine \(0\) oder \(1\) für ein Zeichen an einer zufälligen Stelle erhalten. Das ändert sich jedoch nicht wenn wir die Wortlänge auf \(2\) erhöhen. Es ergibt sich \(H_2 = 1\), denn mit Wahrscheinlichkeit \(0.5\) sehen wir entweder \(1,0\) oder \(0,1\). Wäre die Folge rein zufällig, wäre \(H_2 = 2\), denn mit Wahrscheinlichkeit \(0.25\) sähen wir \(0,0\) oder \(0,1\) oder \(1,0\) oder \(1,1\). Es ergibt sich:

\[H_2 = 4 \cdot 0.25 \cdot \log_2(4) = \log_2(4) = 2\]

Für unsere Folge \(0,1,0,1,0,1, \ldots\) entscheidet das erste Zeichen über alle weitere Zeichen, egal wie lang das Wort ist, welches wir betrachten. Somit ist die Entropie \(H_n = 1\) und damit

\[H = \lim_{n \rightarrow \infty} \frac{H_n}{n} = \lim_{n \rightarrow \infty} \frac{1}{n} = 0.\]

Der Informationsgehalt ist gering und wir könnten mit deutlich weniger Zeichen, die gleiche Information übertragen! Die rein zufällige Folge aus \(0\) und \(1\) steht im Gegensatz dazu und enthält sehr viel Information, denn

\[H_n = \log(2^n) = n\]

und damit gilt

\[H = \lim_{n \rightarrow \infty} \frac{H_n}{n} = \lim_{n \rightarrow \infty} \frac{n}{n} = 1.\]

Bei Shannons Informationsbegriff gehen wir davon aus, dass Information in kleinste Informationsteile (Bits) zerlegbar ist. Zudem ist die Summe dieser Teilchen die Information selbst. Beim Zusammensetzen der Einzelteile, also der Kombination von Symbolen, entsteht demnach keine neue Qualität, welche eben nicht auf die einzelnen Symbole reduziert werden kann.

Information (Informatik)

Eine Information ist eine übertragene Nachricht und kann als die Summe ihrer Einzelteile betrachtet werden.

Shannons Informationsbegriff ignoriert jedwede Semantik und verdinglicht die Information, dennoch ist er aus technischer Sicht sehr nützlich. Er hilft uns zu bestimmen wie viel Zeichen (Syntax) notwendig sind, um etwas auszudrücken. Eine hohe Entropie bedeutet in diesem Zusammenhang, dass wir unsere Zeichen sparsam nutzen. Außerdem kann die Entropie als Informationsgehalt aus Sicht der digitalen Maschine verstanden werden, da sie keinerlei Semantik a priori kennt. Zwar kann der Computer, zum Beispiel zwei Binärzahlen addieren, doch hat er keinerlei Vorstellung vom Gegenstand der Zahl. Alle Manipulationen sind syntaktischer Natur, d.h., eine Manipulation von Zeichen.

Formale Methoden

Formale Methoden sind unter anderem eine Anstrengung, um wesentliche semantische Aspekte von Sprache und dem Denken auf regelgeleitete, rein syntaktische Symbolmanipulation zurückzuführen.

8.2.2. Informationstheorie#

Verlassen wir die Sicht der Nachrichtenübertragung, so hilft uns der klassische Informationsbegriff von Shannon nicht sonderlich weiter. Wie etwa unterscheidet sich der Informationsgehalt von einer zufälligen Bitfolge der Länge \(n\) zu einer angenäherten Darstellung der Kreiszahl \(\pi\) beschränkt auf \(n\) Bits? In Shannons Theorie agiert ein Zusammenschluss von Akteuren (Sender, Empfänger, Kanal, Nachricht). Um seinen Informationsbegriff auf eine einzelne Zeichenkette zu nutzten, müssten wir uns irgendwie einen künstlichen Nachrichtenkanal und Sender konstruieren.

Anstatt der Perspektive aus der Nachrichtenübertragung betrachtet die algorithmische Informationstheorie, mithilfe der Kolmogorow-Komplexität, die algorithmische Beschreibung einer Zeichenfolge. Die Kolmogorow-Komplexität einer Zeichenkette ist die Länge ihrer kürzesten Beschreibung in Form eines Algorithmus. Je kürzer der Algorithmus bzw. die Beschreibung, desto weniger Information enthält die durch ihn erzeugte/beschriebene Zeichenkette.

Kolmogorow-Komplexität

Für eine Programmiersprache \(U\), z.B. beschrieben als universelle Turingmaschine, ist der Informationsgehalt oder Kolmogorow-Komplexität \(C_U(w)\) einer Zeichenfolge \(w\) definiert als die Bitlänge des kürzesten Programms \(T\) (z.B. Turingmaschine), das ohne weitere Eingabe die Zeichenfolge \(w\) als Ausgabe erzeugt. Mathematisch ausgedrückt:

\[C_U(w) = \min\limits_{\alpha_T\in\mathbb{B}^*} \left\{ |\alpha_T| : U(\alpha_T) = T() = w\right\},\]

wobei \(T()\) bedeutet, dass die Turingmaschine \(T\), welche durch \(\alpha_T\) beschrieben ist, ohne Eingabe startet. \(|\alpha_T|\) ist die Länge der Beschreibung der Turingmaschine \(T\).

Nehmen wir an wir möchten folgende Zeichenkette

\[\text{abababababababababab}\]

also 10 mal die Zeichen \(\text{ab}\) beschreiben. In Python können wir das mit folgendem Algorithmus vollziehen:

'abababababababababab'

'abababababababababab'

Dieser Algorithmus benötigt insgesamt 22 Zeichen. Allerdings ist das nicht das kürzeste Programm. Folgender Algorithmus/Beschreibung

'ab'*10

'abababababababababab'

benötigt lediglich 7 Zeichen und erzeugt die gleiche Zeichenkette. Wie sieht es nun aus wenn wir aus dem mittleren \(\text{a}\) ein \(\text{b}\) machen? Wenn wir also

\[\text{ababababaaababababab}\]

beschreiben wollen? Folgendes Python-Programm erzeugt die neue Zeichenkette:

'ab'*4+'aa'+5*'ab'

'ababababaaababababab'

Wären wir uns sicher, dass die angegebenen Algorithmen die kürzesten Beschreibungen sind, so können wir sagen dass \(\text{abababababababababab}\) weniger Information enthält als \(\text{ababababaaababababab}\). Löschen wir ein \(\text{a}\) aus der ursprünglichen Zeichenkette, z.B. \(\text{ababbababababababab}\) so müssen wir den Python-Code wie folgt anpassen:

'ab'*2+'b'+7*'ab'

'ababbababababababab'

Obwohl die Zeichenkette kürzer ist, enthält sie mehr Information. Kürzere Zeichenketten können nach dieser Definition mehr Informationen enthalten als längere, entscheidend ist deren Beschreibungslänge.

Die kürzeste Beschreibung kann nicht länger als die nicht-algorithmische Beschreibung der Zeichenkette sein. Das bedeutet, wir können immer die Zeichenkette in Form einer Programmiersprache niederschreiben, so wie wir das ganz zu Beginn getan haben.

Algorithmische Zufälligkeit

Falls die Länge der kürzesten Beschreibung einer Zeichenkette größer oder gleich der Länge der Zeichenkette selbst ist, so nennen wir diese Zeichenkette algorithmisch zufällig und unkomprimierbar.

Problematisch an der Kolmogorow-Komplexität und im Gegensatz zur Entropie gilt, dass wir sie im Allgemeinen nicht berechnen können.

Unberechenbarkeit der Kolmogorow-Komplexität

Sei eine beliebige Zeichenkette \(w\) und eine Programmiersprache \(U\) gegeben, so ist die Kolmogorow-Komplexität \(C_U(w)\) im Allgemeinen nicht berechenbar.

Haben wir eine bestimmte Beschreibung für eine Zeichenkette, könnte es immer eine noch kürzere Beschreibung geben. Wir können jedoch immer eine Obergrenze für die Kolmogorow-Komplexität bestimmen.

Außerdem kann man zeigen, dass für zwei universelle Turingmaschinen \(U\) und \(U'\) sich \(C_U(w)\) und \(C_{U'}(w)\) für alle \(w\) maximal um eine additive Konstante unterscheiden (Theorem der Invarianz). Das geht aus der Komplexitätstheorie hervor. Somit ist die Kolmogorow-Komplexität von den verwendeten Modellierungsmitteln, z.B. Programmiersprachen, weitestgehend unabhängig.

Durch die Kolmogorow-Komplexität wechseln wir die Perspektive von der Nachricht zu ihrer Konstruktion durch einen Algorithmus. Wir suchen den kürzesten Algorithmus / die kürzeste Beschreibung für die Erzeugung einer Zeichenkette. Daraufhin analysieren wir nicht die Information selbst, sondern jenen Algorithmus. Je kürzer der Algorithmus, desto geringer der Informationsgehalt.

Eine Komprimierung ist eine algorithmische Beschreibung (Programm) einer Zeichenkette, welche kürzer als die Zeichenkette ist und diese erzeugt. Aus Sicht der Kolmogorow-Komplexität enthält ein 3000-seitiges Lexikon weniger Informationen als eine gleich lange, rein zufällig generierte Zeichenkette, obwohl das Lexikon selbstverständlich viel nützlicher ist. Wir könnten aus den Wörtern des Lexikons bestimmte Zeichenfolgen komprimieren. Für die zufällige Folge an Zeichen ist dies nicht möglich.

Auch dieser Begriff bezieht nur die Syntax einer vorliegenden Information ein. Die Semantik wird erneut ausgeklammert.