16.6. Rekursive Funktionen#
Bevor Sie fortfahren sollten Sie sich den Abschnitt Wiederholung durchgelesen haben.
Wir werden in diesem Abschnitt nicht über Rekursion an sich sprechen, sondern wie rekursive Funktionen in den allermeisten Programmiersprachen realisiert werden.
Wie realisiert der Computer Rekursion?
Was passiert bei einem rekursiven Aufruf?
Und was sind überhaupt rekursive Funktionen?
Rekursive Funktionen
Als rekursive Funktion wird eine Funktion bezeichnet, welche sich für bestimmte Argumente selbst aufruft.
Die folgende Berechnung der Fakultät ist eine rekursive Funktion, welche wir bereits eingeführt hatten.
def fac(n):
if n <= 1: # Base cases!
return 1
else: # Recursive case
return n * fac(n-1) # Recursive call
fac(4)
24
Damit eine rekursive Funktion terminiert benötigt sie mindestens einen Basisfall, d.h. einen Pfad an Anweisungen, welcher keinen Funktionsaufruf der Funktion selbst enthält. Das ist eine notwendige aber noch nicht hinreichende Bedingung. Um formal zu beweisen, dass eine rekursive Funktion terminiert und auch das richtig berechnet, verwendet man die sog. Induktion.
Im obigen Fall sehen wir recht schnell, dass alles korrekt ablaufen sollte, sofern n eine natürliche Zahl ist.
Da wir n bei jedem rekursiven Aufruf um 1 verkleinern, muss irgendwann die if-Bedingung zutreffen.
In anderen Worten kommen wir immer irgendwann in den Basisfall!
Wie aber werden die Variablen der unterschiedlichen Funktionsaufrufe verwaltet?
Gibt es nur ein einzelnes n, welches von allen Funktionsaufrufen verwendet wird?
Dieser Punkt ist äußerst wichtig.
Lassen Sie uns den Funktionsaufruf fac(4) einmal ‚ausbreiten‘:
fac(4) wird zu 4 * fac(3) wird zu 4 * fac(2) wird zu 4 * 3 * fac(1) wird schließlich zu 4 * 3 * 2 * 1.
16.6.1. Stack und Heap#
Es ist äußerst wichtig zu begreifen, dass bei jedem rekursiven Aufruf ein neuer lokaler Namensraum eröffnet wird! Das bedeutet, jeder Funktionsaufruf verwendet einen frischen Satz an Variablen. Dieser Namensraum befindet sich auf dem sog. Stack, zu deutsch Stapel.
Stack (Arbeitsspeicher)
Der Stack ist ein spezieller Bereich des Arbeitsspeichers, auf welchem die Variablen des lokalen Namensraums liegen.
Bei jedem Funktionsaufruf wird ein Namensraum automatisch auf den Stack gelegt und bei jedem Rücksprung (return) wird der entsprechende Namensraum automatisch vom Stack gelöscht.
Immer wenn wir fac aufrufen, wird ein neuer lokaler Namensraum auf den Stack gelegt.
Dieser enthält die Variable n.
Da die Funktionen rekursiv aufgerufen werden, füllt sich der Stack bis wir uns im Aufruf von fac(1) befinden.
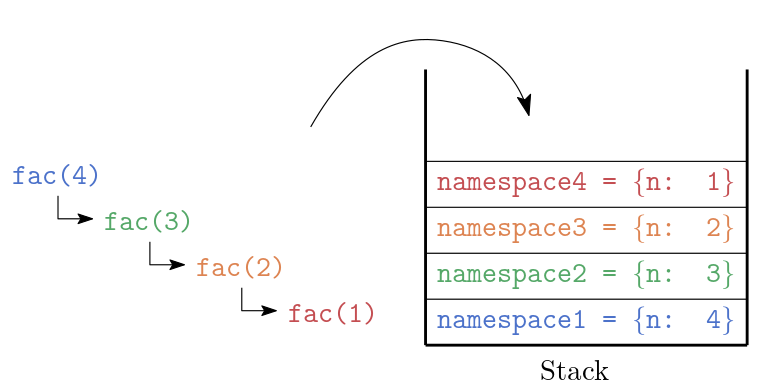
Abb. 16.1 Befüllung des Stacks durch den Aufruf der rekursiven Funktion fac(4).#
fac(1) gelangt in den Basisfall und beendet die Rekursionskette.
Es ließt sein n aus seinem Namensraum (in Abbildung 16.1 ist das der namespace4), prüft n <= 1 und liefert 1 zurück.
Durch diesen Rücksprung, wird der Namensraum gelöscht und der nächste Namensraum auf dem Stack definiert den Namensraum des aktuellen Funktionsaufrufs.
In diesem hat n den Wert 2 und wir befinden uns bereits an der Stelle return n * fac(1) und da fac(1) soeben den Wert 1 zurückgeliefert hat, wird dieser Ausdruck zu return n * 1 und somit zu return 2 * 1.
Sukzessive leert sich der Stack.
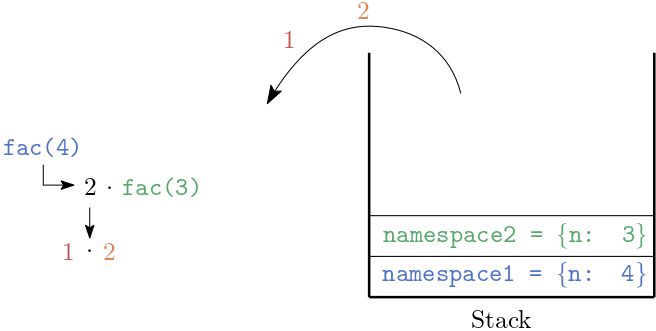
Abb. 16.2 Der Stacks leert sich beim Rücksprung.#
Wann immer eine Funktion aufgerufen wird (egal ob rekursiv oder nicht) wird oben auf dem Stack ein Speicherblock für den lokalen Namensraum reserviert und wann immer die Funktion terminiert/zurückspringt der Speicherblock wird wieder freigegeben. Der Zugriff auf den Stack ist schnell, da die Reservierung und das Freigeben wenig Verwaltungsinformation benötigt. Außerdem ist der Stack ein zusammenhängender Speicherbereich, d.h., aufeinanderfolgende Speicherzugriffe liegen nahe im Speicher beisammen.
Stack und Funktionsaufrufe
Damit wir als Programmierer*innen Codeblöcke aus Gründen der Laufzeit Funktionen vermeiden, muss der Stack sehr effizient sein!
Die maximale Tiefe des Stacks ist an eine bestimmte Zahl gebunden. Ist unsere Rekursion zu tief, läuft der Stacks voll:
fac(1000)
402387260077093773543702433923003985719374864210714632543799910429938512398629020592044208486969404800479988610197196058631666872994808558901323829669944590997424504087073759918823627727188732519779505950995276120874975462497043601418278094646496291056393887437886487337119181045825783647849977012476632889835955735432513185323958463075557409114262417474349347553428646576611667797396668820291207379143853719588249808126867838374559731746136085379534524221586593201928090878297308431392844403281231558611036976801357304216168747609675871348312025478589320767169132448426236131412508780208000261683151027341827977704784635868170164365024153691398281264810213092761244896359928705114964975419909342221566832572080821333186116811553615836546984046708975602900950537616475847728421889679646244945160765353408198901385442487984959953319101723355556602139450399736280750137837615307127761926849034352625200015888535147331611702103968175921510907788019393178114194545257223865541461062892187960223838971476088506276862967146674697562911234082439208160153780889893964518263243671616762179168909779911903754031274622289988005195444414282012187361745992642956581746628302955570299024324153181617210465832036786906117260158783520751516284225540265170483304226143974286933061690897968482590125458327168226458066526769958652682272807075781391858178889652208164348344825993266043367660176999612831860788386150279465955131156552036093988180612138558600301435694527224206344631797460594682573103790084024432438465657245014402821885252470935190620929023136493273497565513958720559654228749774011413346962715422845862377387538230483865688976461927383814900140767310446640259899490222221765904339901886018566526485061799702356193897017860040811889729918311021171229845901641921068884387121855646124960798722908519296819372388642614839657382291123125024186649353143970137428531926649875337218940694281434118520158014123344828015051399694290153483077644569099073152433278288269864602789864321139083506217095002597389863554277196742822248757586765752344220207573630569498825087968928162753848863396909959826280956121450994871701244516461260379029309120889086942028510640182154399457156805941872748998094254742173582401063677404595741785160829230135358081840096996372524230560855903700624271243416909004153690105933983835777939410970027753472000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
Wir können die maximale erlaubte Rekursionstiefe auch anpassen:
import sys
sys.setrecursionlimit(5000)
fac(1000)
402387260077093773543702433923003985719374864210714632543799910429938512398629020592044208486969404800479988610197196058631666872994808558901323829669944590997424504087073759918823627727188732519779505950995276120874975462497043601418278094646496291056393887437886487337119181045825783647849977012476632889835955735432513185323958463075557409114262417474349347553428646576611667797396668820291207379143853719588249808126867838374559731746136085379534524221586593201928090878297308431392844403281231558611036976801357304216168747609675871348312025478589320767169132448426236131412508780208000261683151027341827977704784635868170164365024153691398281264810213092761244896359928705114964975419909342221566832572080821333186116811553615836546984046708975602900950537616475847728421889679646244945160765353408198901385442487984959953319101723355556602139450399736280750137837615307127761926849034352625200015888535147331611702103968175921510907788019393178114194545257223865541461062892187960223838971476088506276862967146674697562911234082439208160153780889893964518263243671616762179168909779911903754031274622289988005195444414282012187361745992642956581746628302955570299024324153181617210465832036786906117260158783520751516284225540265170483304226143974286933061690897968482590125458327168226458066526769958652682272807075781391858178889652208164348344825993266043367660176999612831860788386150279465955131156552036093988180612138558600301435694527224206344631797460594682573103790084024432438465657245014402821885252470935190620929023136493273497565513958720559654228749774011413346962715422845862377387538230483865688976461927383814900140767310446640259899490222221765904339901886018566526485061799702356193897017860040811889729918311021171229845901641921068884387121855646124960798722908519296819372388642614839657382291123125024186649353143970137428531926649875337218940694281434118520158014123344828015051399694290153483077644569099073152433278288269864602789864321139083506217095002597389863554277196742822248757586765752344220207573630569498825087968928162753848863396909959826280956121450994871701244516461260379029309120889086942028510640182154399457156805941872748998094254742173582401063677404595741785160829230135358081840096996372524230560855903700624271243416909004153690105933983835777939410970027753472000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
Der andere Speicherbereich, welcher nicht zum Stack gehört, bezeichnen wir als Heap.
Heap (Arbeitsspeicher)
Der Heap ist ein Speicherbereich für die dynamische Speicherverwaltung. Anders als beim Stack gibt es kein Muster mit dem der Heap gefüllt bzw. geleert werden muss.
Im Heap kann man kreuz und quer Speicher reservieren und freigeben. Das macht die Verwaltung des Heaps komplexer. Im Vergleich zum Stack ist es deutlich aufwendiger zu protokollieren, welche Speicherbereiche frei und welche belegt sind.
16.6.2. Laufzeit#
Obwohl der Stack enorm effizient ist, sind iterative Lösungen fast immer schneller in ihrer Ausführung. Übersetzten wir den Code in Maschinencode, also in die niedrigste bzw. konkreteste Form, so benötigen rekursive Lösungen fast immer mehr Sprungbefehle.
Auch benötigt ein Funktionsaufruf mehr Ressourcenmanagement als ein Sprung zum Anfang einer Schleife. Vergleichen wir unsere rekursive Lösung mit der iterativen:
def fac_it(n):
result = 1
for i in range(1,n+1):
result += i
return result
Die iterative Lösung verwendet lediglich drei Variablen nämlich n, i und result, wohingegen wir bei der rekursiven Lösung für fac(n) ca. n Variablen benötigen.
Zusätzlich sind CPU’s in der von Neumann Architektur auf Schleifen optimiert. Rücksprünge kann die CPU nur vorhersagen, wenn es von ihnen nicht zu viele hintereinander gibt. Dazu verwendet die CPU einen begrenzten Speicher. Läuft dieser voll, schlägt die Vorhersage fehl und die Ausführungszeit verlängert sich drastisch.
Lassen Sie uns die Laufzeiten der beiden Implementierungen vergleichen:
%timeit fac_it(1000)
22.3 µs ± 44.5 ns per loop (mean ± std. dev. of 7 runs, 10,000 loops each)
%timeit fac(1000)
393 µs ± 1.53 µs per loop (mean ± std. dev. of 7 runs, 1,000 loops each)
Der rekursive Aufruf benötigt ca. 473 Nanosekunden, wohingegen die iterative Berechnung ca. 60 Nanosekunden benötigt. Das heißt die iterative Berechnung ist um einen Faktor von
schneller!
16.6.3. Endrekursionen (in Python?)#
Der Laufzeitvergleich hängt jedoch auch mit der verwendeten Programmiersprache zusammen. Funktionale Sprachen bieten, zum Beispiel, das Konzept der optimierten Endrekursion (engl. Tail Recursion).
Endrekursion
Endrekursion ist eine bestimmte Form der Rekursion bei der der rekursive Aufruf einer Funktion auch ihre letzte Anweisung ist.
Ist eine Funktion endrekursiv, eliminieren die Compiler oder Interpreter von funktionalen Sprachen die rekursiven Aufrufe der Funktion – der Stack bleibt (bis auf einen Eintrag) leer.
Unsere fac-Funktion ist keine Endrekursion, denn nach dem rekursiven Aufruf folgt eine Multiplikation.
Wir können daraus jedoch leicht eine Endrekursion machen:
def fac_tail(n, acc=1):
if n <= 1:
return acc
else:
return fac_tail(n-1, acc*n)
fac_tail(4)
24
Alle Arbeit ist getan und dann folgt der rekursive Aufruf.
Deshalb können wir eigentlich alle Namensräume, welche auf dem Stack liegen vergessen.
Wir haben n bereits verarbeitet und brauchen es nicht mehr.
Deshalb belastet diese Rekursion den Stack nicht, sofern unser Compiler oder Interpreter dies auch optimiert.
Endrekursion in Python
Der Python-Interpreter nutzt die Endrekursion nicht aus.
Der Python-Interpreter optimiert dies nicht!
D.h. obwohl wir n vergessen könnten, wird es auf den Stack gelegt.
Warum sich die Entwickler*innen gegen elimination von Endrekursionen (engl. Tail Recursion Elimination (TRE)) entschieden haben, hat verschiedene Gründe:
TRE zerstört den sog. Stack Trace (wichtig für Fehlermeldungen)
TRE als Option würde Entwickler*innen motivieren die Rekursion häufiger zu verwenden, doch würde der Code dann nicht überall gleich effizient laufen
Entwickler*innen von
Pythonglauben nicht an die Rekursion als Basis jeder ProgrammierungIn
Pythonwäre die Realisierung durch dessen Dynamik äußerst kompliziert, hier ein einfaches Beispiel was bereits zu Problemen führt:
def f(x):
if x > 0:
return f(x-1)
return 0
g = f
def f(x):
return x
g(5)
4
Wir binden g an das erste f.
Dann aber definieren wir f neu.
g(5) ruft das alte f auf, nennen wir es f_old.
Somit wird g(5) zu f_old(5).
Diese Funktion ruft nun das nicht rekursive neue f auf, d.h. f(5-1) wird zu f(4) wird zu 4.
Wie soll der Interpreter protokollieren welche Funktionen rekursiv sind und welche nicht oder nicht mehr?
Dadurch, dass wir Funktionsnamen in Python zur Laufzeit ändern können, wäre dies unglaublich aufwendig.
An diesem Beispiel wird deutlich, dass die Flexibilität und Dynamik einer Sprache ihren Preis hat. Für Interpreter und Compiler wird es schwerer und schwerer Optimierungen durchzuführen!

