7.3. Repräsentationen

Bevor wir genauer darauf eingehen wie der Informationskreislauf vollzogen wird, müssen wir uns ansehen wie Computer unterschiedliche Arten von Information (Text, Ton, Bild, usw.) repräsentieren.

7.3.1. Das Binärsystem

Computer arbeiten auf der Basis von zwei Zuständen (0 und 1). Salopp sagt man auch, dass sie die Binärsprache „sprechen“. Da die kleinste Informationseinheit, das Bit, nur zwei Zustände annehmen kann, sind die Operationen äußerst simpel. Die Komplexität und die damit einhergehende Rechenfähigkeit entsteht durch das Kombinieren und Hintereinanderschalten von Millionen dieser Operationen.

Als Computational Thinker*innen kümmern wir uns kaum um die genaue Manipulation der Bits und Bytes. Wir Abstrahieren diese Aufgabe durch Programmiersprachen, die uns weitaus komfortablere Möglichkeiten bieten. Dennoch sind diese Informationseinheiten und deren Manipulation von wesentlicher Bedeutung, um die Funktionsweise eines Computers zu verstehen.

In einem Computer befinden sich mikroskopisch kleine Leitungen und Schaltkreise, welche alle Informationen eines Computers speichern, übertragen und verarbeiten. Anstatt 0 und 1 verwendet der Computer also eigentlich elektrische Signale bzw. Spannungen, gespeichert in Milliarden von Transistoren und übertragen durch sog. Bus-Systeme (Leitungen/Kabel).

Wie aber lassen sich Informationen mit solchen elektrischen Signalen darstellen? Stellen wir uns eine Lampe mit zwei Zustände vor. Die Lampe ist entweder aus (0) oder sie ist an (1).

Abb. 7.2 Eine Lampe die entweder aus (links) oder an (rechts) geschaltet sein kann.

Entweder es fließt Strom hindurch, was dem Zustand 1 entspricht, oder es fließt kein Strom hindurch, was den Zustand 0 darstellt.

Natürlich könnte man mehr Zustände darstellen indem man misst wie viel Strom fließt oder wie viel Spannung angesetzt ist. Es hat sich aber herausgestellt, dass das einfache Strom an und Strom aus robuster, sicherer und effizienter ist. So lassen sich die zwei Zustände sehr einfach unterscheiden.

Mit Strom an, Strom aus können wir durch eine Interpretation zum Beispiel folgende Mengen repräsentieren:

Strom aus	Strom an
\(0\)	\(1\)
falsch	wahr
nein	ja
weiß	schwarz

Mit einer Lampe können wir jede zweielementige Menge repräsentieren. Der einzelne Zustand einer Lampe, also Strom aus oder Strom an nennen wir Bit. Es ist die kleinst mögliche Einheit an Information welche ein Computer speichern und verarbeiten kann.

Bit

Der einzelne Zustand eines Kabels oder einer Lampe, also Strom aus oder Strom an nennen wir Bit. Es ist die kleinst mögliche Einheit an Information welche ein Computer speichern und verarbeiten kann.

Benutzen wir mehrere (geordnete) Lampen so erhalten wir mehrere Bits und können so komplexere Informationen speichern. Mit zwei Lampen können wir bereits vier Zustände:

\[(0,0), (0,1), (1,0) \text{ und } (1,1).\]

darstellen. Mit drei Lampen sind es bereits acht:

\[(0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0), (1,1,1).\]

Mit jeder weiteren Lampe verdoppelt sich die Anzahl der repräsentierbaren Zustände. Und somit können wir mit \(n\) Lampen eine Menge mit \(2^n\) Elementen repräsentieren. Dieser exponentielle Anstieg ist enorm wichtig. Ohne diese Eigenschaft würden die Speicher der Computer sehr schnell volllaufen.

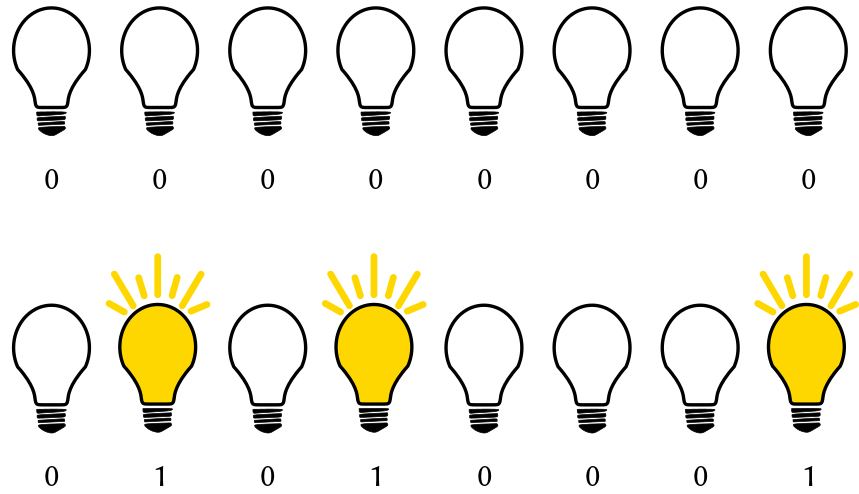
Abb. 7.3 Zwei der \(2^8 = 256\) möglichen Zustände von acht Lampen.

Weshalb verwenden wir aber kein Zahlensystem mit drei oder mehr Zuständen? Wie oben erwähnt ist es aus technischer Sicht bisher deutlich einfacher und effizienter mit nur zwei Zuständen zu arbeiten. Zudem ist die Einsparung, die wir durch mehr Zustände erzielen würden, unwesentlich.

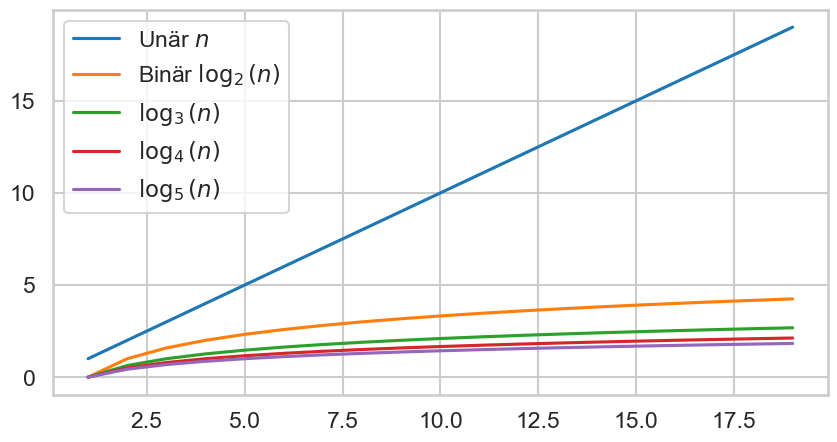
Wir könnten auch mit nur einem Zustand, z.B. Strom aus, Informationen repräsentieren. Diese sog. Unärsystem verwenden wir Menschen, wenn wir mit den Händen zählen. Das System ist allerdings für größere Datenmengen ungeeignet, da wir für eine Menge mit \(n\) Elementen \(n\) Bits bräuchten, um diese zu repräsentieren. Wechseln wir zu einem System mit drei Zuständen, bräuchten wir im Vergleich zum Binärsystem noch weniger Bits, doch ist das was wir gewinnen unwesentlich. Der Grund dafür ist das Verhalten des Logarithmus.

Der folgende Plot illustriert wie viele Bits (y-Achse) für eine Menge mit \(n\) Elementen (x-Achse) im jeweiligen Zahlensystem notwendig sind. Der Unterschied zwischen Binär und Unär ist enorm, wohingegen der Unterschied zwischen Binär und, zum Beispiel, \(\log_5(n)\), also die Verwendung von 5 unterschiedlichen Zuständen, gering ist. Dies folgt aus den Rechengesetzen des Logarithmus:

\[\log_a(x) = \frac{\log_b(x)}{\log_b(a)}\]

wobei \(\log_b(a)\) eine Konstante ist.

7.3.2. Zahlen im Binärsystem

Werfen wir einen genaueren Blick aufs Binärsystem, auch binäre Zahlensystem genannt. Um Zahlen mit Strom an und Strom aus, also den zwei Zuständen einer Lampe/Transistors/Bit zu repräsentieren, verwenden Computer das Binärsystem.

Notation verschiedener Zahlensysteme

Um der Verwirrung vorzubeugen notieren wir eine Zahl \(k\), geschrieben in der Dezimaldarstellung, auch durch \(k_{10}\) und eine Zahl \(b\) in der Binärdarstellung durch \(b_2\).

7.3.2.1. Natürliche Zahlen

In dem für Sie intuitiven Dezimalsystem schreiben wir eine Zahl mit den Ziffern \(0, 1, 2, 4, 5, 6, 7, 8, 9\) und verwenden eine Basis von \(10\). Zum Beispiel ist \(1871\) gleich

\[1 \cdot 10^3 + 8 \cdot 10^2 + 7 \cdot 10^1 + 1 \cdot 10^0.\]

Die Zahl, beschrieben als Folge von Ziffern \(d_{n-1} \ldots d_0\) mit \(d_i \in \{0,1,2,3,4,5,6,7,8,9\}\), hat den Wert

(7.1)\[d_{n-1} \ldots d_0 = d_{\class{hm-lightblue} n\class{hm-lightblue}-\class{hm-lightblue}1} \cdot 10^{\class{hm-lightblue} n\class{hm-lightblue}-\class{hm-lightblue}1} + \ldots + d_{\class{hm-lightblue} 0} \cdot 10^{\class{hm-lightblue} 0} = \sum\limits_{{\class{hm-lightblue} i}=0}^{n-1} d_{\class{hm-lightblue} i} \cdot 10^{\class{hm-lightblue} i}.\]

Im Binärsystem verwenden wir hingegen lediglich die Ziffern \(0, 1\) und die Basis \(2\). Eine Zahl als Folge von Ziffern \(b_{n-1} \ldots b_0\) mit \(b_i \in \{0,1\}\) hat den Wert

(7.2)\[ b_{n-1} \ldots b_0 = b_{\class{hm-lightblue} n\class{hm-lightblue}-\class{hm-lightblue}1} \cdot 2^{\class{hm-lightblue} n\class{hm-lightblue}-\class{hm-lightblue}1} + \ldots + b_{\class{hm-lightblue} 0} \cdot 2^{\class{hm-lightblue} 0} = \sum\limits_{{\class{hm-lightblue} i}=0}^{n-1} b_{\class{hm-lightblue} i} \cdot 2^{\class{hm-lightblue} i}.\]

Zum Beispiel hat \(1101_2\) den Wert

\[1 \cdot 2^3 + 1 \cdot 2^2 + 0 \cdot 2^1 + 1 \cdot 2^0 = 8 + 0 + 0 + 1 = 13.\]

\(1001_2\) (binär) und \(13_{10}\) (dezimal) repräsentieren den gleichen numerischen Wert, lediglich ihre Darstellung—ihr Repräsentant—ist ein anderer. Würden Sie fließend Binär sprechen, bräuchten Sie keinerlei Berechnungen um zu wissen welchen Wert \(1001_2\) repräsentiert.

# Transformation einer Zahl in Binärdarstellung zu ihrer Decimaldarstellung
def to_decimal(binary_number):
    decimal_number = 0
    i = len(binary_number)-1
    for bit in binary_number:
        decimal_number += bit * 2**i
        i += -1
    return decimal_number
# Zahl in Binärdarstellung 111 0100 1111 wird umgewandelt
to_decimal([1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1])

1871

Ok, wir können also eine Binärzahl (= Zahl in Binärdarstellung) recht einfach in eine Dezimalzahl umwandeln. Wie aber wandeln wir eine Dezimalzahl in eine Binärzahl um?

Nehmen wir als Beispiel die Dezimalzahl \(9\). Wir suchen eine Binärzahl \(b_{n-1}\ldots b_0\), sodass

(7.3)\[b_{n-1} \cdot 2^{n-1} + \ldots + b_0 \cdot 2^0 = 9\]

ergibt. Was passiert wenn wir in Gleichung (7.3) beide Seiten durch \(2\) dividieren?

\[\begin{split} \begin{split} b_{n-1} \cdot 2^{n-1} + \ldots + b_0 \cdot 2^0 &= 9 \iff \\ \left( b_{n-1} \cdot 2^{n-1} + \ldots + b_0 \cdot 2^0 \right) / 2 &= 9 / 2 \iff \\ b_{n-1} \cdot 2^{n-2} + \ldots + b_1 \cdot 2^0 + b_0 / 2 &= 4 + 1 / 2 \iff \end{split}\end{split}\]

Der Ausdruck

\[b_{n-1} \cdot 2^{n-2} + \ldots + b_1 \cdot 2^0\]

muss eine ganze Zahl ergeben. Zudem wissen wir, dass \(b_0\) entweder den Wert \(0\) oder \(1\) annimmt. Es folgt unweigerlich, dass

\[b_0 / 2 = 1 / 2 \Rightarrow b_0 = 1\]

und

\[b_{n-1} \cdot 2^{n-2} + \ldots + b_1 \cdot 2^0 = 4.\]

Wir können erneut durch zwei dividieren und erhalten:

\[b_{n-1} \cdot 2^{n-3} + \ldots + b_2 \cdot 2^0 + b_1 / 2 = 2.\]

Demnach muss \(b_1 = 0\) sein und

\[b_{n-1} \cdot 2^{n-3} + \ldots + b_2 \cdot 2^0 = 2.\]

Wir dividieren erneut durch zwei und erhalten:

\[b_{n-1} \cdot 2^{n-4} + \ldots + b_3 \cdot 2^0 + b_2 / 2 = 1.\]

Erneut muss demnach \(b_2 = 0\) sein. Schließlich dividieren wir ein letztes Mal mit 2 und erhalten:

\[b_{n-1} \cdot 2^{n-5} + \ldots + b_3 / 2 = 1/2.\]

Demnach muss \(b_3 = 1\) gelten. Alle höherwertigen Bits nehmen den Wert \(0\) an. Zusammenfassend ist demnach

\[1 \cdot 2^3 + 0 \cdot 2^2 + 0 \cdot 2^1 + 1 \cdot 2^0 = 9_{10} = 1001_2\]

Dieser Vorgang scheint komplizierter als er in Wirklichkeit ist. Wir müssen lediglich die sog. Restwertdivision immer und immer wieder anwenden. Wir dividieren die gegebene Dezimalzahl mit 2. Ergibt dies einen Rest, notieren wir eine 1 andernfalls eine 0.

Machen wir noch ein Beispiel und nehmen unsere obige Zahl \(1871\):

\[\begin{split} \begin{split} 1871 &= 935 \cdot 2 + {\class{hm-lightblue} 1} \cdot 2^0 \\ 935 &= 467 \cdot 2 + {\class{hm-lightblue} 1} \cdot 2^0 \\ 467 &= 233 \cdot 2 + {\class{hm-lightblue} 1} \cdot 2^0 \\ 233 &= 116 \cdot 2 + {\class{hm-lightblue} 1} \cdot 2^0 \\ 116 &= 58 \cdot 2 + {\class{hm-lightblue} 0} \cdot 2^0\\ 58 &= 29 \cdot 2 + {\class{hm-lightblue} 0} \cdot 2^0\\ 29 &= 4 \cdot 2 + {\class{hm-lightblue} 1} \cdot 2^0\\ 14 &= 7 \cdot 2 + {\class{hm-lightblue} 0} \cdot 2^0\\ 7 &= 3 \cdot 2 + {\class{hm-lightblue} 1} \cdot 2^0 \\ 3 &= 1 \cdot 2 + {\class{hm-lightblue} 1} \cdot 2^0 \\ 1 &= 0 \cdot 2 + {\class{hm-lightblue} 1} \cdot 2^0 \end{split}\end{split}\]

Wir erhalten somit

\[\begin{split} \begin{split} 1871_{10} &= {\class{hm-lightblue}1} {\class{hm-lightblue}1} {\class{hm-lightblue}1} {\class{hm-lightblue}0} {\class{hm-lightblue}1} {\class{hm-lightblue}0} {\class{hm-lightblue}0} {\class{hm-lightblue}1}{\class{hm-lightblue}1}{\class{hm-lightblue}1}{\class{hm-lightblue}1}_2 \\ &= {\class{hm-lightblue} 1} \cdot 2^{10} + {\class{hm-lightblue} 1} \cdot 2^9 + {\class{hm-lightblue} 1} \cdot 2^8 + {\class{hm-lightblue} 0} \cdot 2^7 + {\class{hm-lightblue} 1} \cdot 2^6 + \\ &\quad \, {\class{hm-lightblue} 0} \cdot 2^5 + {\class{hm-lightblue} 0} \cdot 2^4 + {\class{hm-lightblue} 1} \cdot 2^3 + {\class{hm-lightblue} 1} \cdot 2^2 + {\class{hm-lightblue} 1} \cdot 2^1 +{\class{hm-lightblue} 1} \cdot 2^0\\ &= {\class{hm-lightblue} 1} \cdot 1024 + {\class{hm-lightblue} 1} \cdot 512 + {\class{hm-lightblue} 1} \cdot 256 + {\class{hm-lightblue} 0} \cdot 128 + {\class{hm-lightblue} 1} \cdot 64 + \\ &\quad \, {\class{hm-lightblue} 0} \cdot 32 + {\class{hm-lightblue} 0} \cdot 16 + {\class{hm-lightblue} 1} \cdot 8 + {\class{hm-lightblue} 1} \cdot 4 + 1 \cdot 2 + {\class{hm-lightblue} 1} \cdot 1\\ &= 1024 + 512 + 256 + 64 + 8 + 4 + 2 + 1. \end{split}\end{split}\]

Der folgende Python-Code wandelt eine Dezimalzahl in eine Binärzahl (als Liste von 0, 1, gelesen von links nach rechts) um.

# Transformation einer Zahl in Decimaldarstellung zu ihrer Binärdarstellung
def to_binary(number):
    binary_number = []
    while number != 0:
        r = number % 2
        number = number // 2
        binary_number = [r] + binary_number
    return binary_number
# Zahl in Decimaldarstellung wird umgewandelt
to_binary(1871)

[1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1]

7.3.2.2. Ganze Zahlen

Uns steht kein Minus- oder Pluszeichen zur Verfügung. Alles was der Computer kennt sind Bits und Bytes. Wollen wir also anstatt der natürlichen Zahlen die ganzen Zahlen repräsentieren, müssen wir das Vorzeichen irgendwie codieren.

Wollen wir ganze Zahlen repräsentieren so entscheidet das höchste Bit, ob es sich bei der Zahl um eine negative oder positive Zahl handelt. Eine Möglichkeit bestünde darin, dieses höchste Bit als - zu interpretieren, wenn es den Wert 1 hat und als + andernfalls. In diesem Fall könnten wir Gleichung (7.2) verwenden, mit dem Unterschied, dass wir das höchste Bit ausschließen und stattdessen als Vorzeichen interpretieren.

So wäre

\[1011_2 = -011_2 = -3_{10}.\]

Möchte man jedoch mit dieser Codierung rechnen, ergeben sich einige Schwierigkeiten. Zudem verlieren wir ein Bit für das Vorzeichen.

Komplement einer Bitfolge

Das Komplement einer Bitfolge \(b_{n-1} \ldots b_0\), geschrieben als

\[\overline{b_{n-1} \ldots b_0},\]

erhalten wir indem wir jedes Bit, mit dem Wert \(0\), mit einem Bit, mit dem Wert \(1\), und jedes Bit, mit dem Wert \(1\), mit einem Bit, mit dem Wert \(0\), ersetzten.

Anstatt das Vorzeichen und den Betrag als getrennte Teile der Binärfolge zu codieren bietet das sogenannte Zweierkomplement, oder auch 2-Komplement, die bevorzugte Codierung für negative Zahlen. Das höchste Bit wird dabei nicht als Vorzeichen, sondern als negativer Anteil interpretiert.

So ist

\[1011_2 = -2^3 \cdot 1 + 2^2 \cdot 0 + 2^1 \cdot 1 + 2^0 \cdot 1 = -8 + 2 + 1 = -5\]

und

\[111_2 = -2^2 \cdot 1 + 2^1 \cdot 1 + 2^0 \cdot 1 = -4 + 2 + 1 = -1.\]

Aus Gleichung (7.2) wird

(7.4)\[\begin{split} \begin{split} b_{n-1} \ldots b_0 &= -b_{\class{hm-lightblue} n\class{hm-lightblue}-\class{hm-lightblue}1} \cdot 2^{\class{hm-lightblue} n\class{hm-lightblue}-\class{hm-lightblue}1} + b_{\class{hm-lightblue} n\class{hm-lightblue}-\class{hm-lightblue}2} \cdot 2^{\class{hm-lightblue} n\class{hm-lightblue}-\class{hm-lightblue}2} + \ldots + b_{\class{hm-lightblue} 0} \cdot 2^{\class{hm-lightblue} 0}\\ &= -b_{\class{hm-lightblue} n\class{hm-lightblue}-\class{hm-lightblue}1} \cdot 2^{\class{hm-lightblue} n\class{hm-lightblue}-\class{hm-lightblue}1} + \sum\limits_{{\class{hm-lightblue} i}=0}^{n-2} b_{\class{hm-lightblue} i} \cdot 2^{\class{hm-lightblue} i}. \end{split}\end{split}\]

Sofern es sich um eine negative Zahl handelt, d.h. \(b_{n-1} = 1\), können wir die Gleichung (7.4) auch umschreiben, indem wir das Komplement eines jeden Bit verwenden. Daher der Name Zweierkomplement:

(7.5)\[\begin{split} \begin{split} b_{n-1} \ldots b_0 &= -\overline{b}_{\class{hm-lightblue} n\class{hm-lightblue}-\class{hm-lightblue}1} \cdot 2^{\class{hm-lightblue} n\class{hm-lightblue}-\class{hm-lightblue}1} - \ldots - \overline{b}_{\class{hm-lightblue} 0} \cdot 2^{\class{hm-lightblue} 0} - 1\\ &= -\left( \sum\limits_{{\class{hm-lightblue} i}=0}^{n-1} \overline{b}_{\class{hm-lightblue} i} \cdot 2^{\class{hm-lightblue} i} \right) - 1, \quad \text{falls} \quad b_{n-1} = 1, \end{split}\end{split}\]

wobei

\[\overline{b} = 1 \iff b = 0\]

gilt.

Dieses System macht es uns enorm einfach eine Zahl \(k\) in eine Zahl \(-k\) umzuwandeln. Sei \(b_{n-1} \ldots b_0\) eine solche Zahl in Binärdarstellung, so ist ihr Komplement plus \(1\), also

\[\overline{b_{n-1} \ldots b_0} + 1\]

gleich \(-k\). Dies gilt sowohl für positive wie auch negative Zahlen \(k\). Zum Beispiel ist \(5_{10} = 0101_2\) und

\[\overline{0101}_2 + 1_2 = 1010_2+1_2 = 1011_2 = -8_{10}+2_{10}+1_{10} = -5_{10}.\]

Zudem gilt:

\[\overline{1011}_2 + 1_2 = 0100_2 + 1_2 = 0101_2 = 5_{10}.\]

Exercise 7.3 (Komplement des Komplements)

Können Sie begründen weshalb für eine Binärzahl \(b_{n-1}\ldots b_0\) folgendes gilt:

\[\overline{\overline{b_{n-1}\ldots b_0} + 1} + 1 = b_{n-1}\ldots b_0.\]

Bei der Rechnung ist die Anzahl der Bits fixiert und es entsteht möglicherweise ein Überlauf.

Solution to Exercise 7.3 (Komplement des Komplements)

Sei \(b_k\) das niedrigste erste Bit welches den Wert \(1\) annimmt. Dann folgt

\[\overline{b_{n-1}\ldots b_0} = \overline{b_{n-1}\ldots b_{k-1}}01\ldots 1.\]

In anderen Worten \(b_k\) wird zu \(0\) und alle niedrigeren Bits nehmen den Wert \(1\) an. Addieren wir nun \(1\) werden alle diese niediederen Bits \(0\) und \(b_k\) nimmt den Wert \(1\) an. Alle höheren Bits bleiben unberührt:

\[\overline{b_{n-1}\ldots b_{k-1}}01\ldots 1 + 1 = \overline{b_{n-1}\ldots b_{k-1}}10\ldots 0\]

Wiederholen wir diesen Vorgang ergibt sich

\[\begin{split} \begin{split} \overline{\overline{b_{n-1}\ldots b_{k-1}}10\ldots 0} + 1 &= b_{n-1}\ldots b_{k-1}\overline{10\ldots 0} + 1\\ &= b_{n-1}\ldots b_{k-1}01\ldots 1 + 1\\ &= b_{n-1}\ldots b_{k-1}10\ldots 0 = b_{n-1}\ldots b_{0}. \end{split} \end{split}\]

Das Bilden des Komplements ist für den Computer eine äußerst einfache und schnelle Operation, siehe Abschnitt Manipulation.

Wichtig ist festzuhalten, dass jede ganze Zahl als Binärzahl dargestellt werden kann! Und da wir jede ganze Zahl als Binärzahl, also als Folge von 0 und 1 darstellen können, können wir all das was wir durch Zahlen repräsentieren können auch durch Strom an und Strom aus endlich vieler Lampen repräsentieren.

7.3.2.3. Addieren (und Subtrahieren)

Im folgenden Abschnitt repräsentieren alle Zahlen in Binärdarstellung ganze Zahlen. Um mit dem Zweierkomplement rechnen zu können müssen wir die Anzahl der Bits fixieren, das heißt, alle Zahlen der Rechnung werden durch gleich viele Bits repräsentiert. Verwenden wir 5 Bits so ist \(00011_2 = 3_{10}\) und \(10011_2 = - 13\). Erzeugen wir einen Überlauf, d. h., bräuchten wir mehr Bits als vorhanden, so werden die höchsten Bits einfach weggelassen.

Mit diesen Annahmen funktioniert die Addition genauso wie Sie es im Dezimalsystem gewohnt sind, wobei \(1_2 + 1_2 = 0_2\) mit dem Übertrag \(1\) ergibt. Addieren wir beispielsweise die zwei 5-Bit Zahlen \(00011_2 = 3_{10}\) und \(00111_2 = 7_{10}\) ergibt dies:

\[\begin{split} \begin{split} 00011_2&\\ +\ \ 00111_2&\\ \hline \hline \text{Übertrag:} \quad 01110_2&\\ \hline \hline = 01010_2&=10_{10} \end{split}\end{split}\]

Wir müssen jedoch Vorsichtig sein! Benötigt das Ergebnis mehr Bits als zu Verfügung stehen, kommt es zu einem Überlauf.

Addieren wir beispielsweise die zwei 5-Bit Zahlen \(01011_2 = 11_{10}\) und \(00111_2 = 7_{10}\) ergibt dies \(010010_2 = 18_{10}\). Doch diese Zahl benötigt 6 Bits. Abgeschnitten ergibt dies deshalb \(10010_2 = -14_{10}\). Dies ist ein unerwünschter Überlauf!

Durch das Zweierkomplement können wir auch negative Zahlen wie gewohnt addieren. Addieren wir beispielsweise \(01011_2 = 11_{10}\) und \(1111_2 = -1_{10}\) ergibt dies:

\[\begin{split} \begin{split} 01011_2&\\ +\ \ 11111_2&\\ \hline \hline \text{Übertrag:} \quad 11110_2&\\ \hline \hline = 101010_2&=18_{10} \end{split}\end{split}\]

Jedoch benötigt \(101010_2\) erneut zu viele Bits. Schneiden wir den Überlauf weg, so ergibt dies \(01010_2 = 10_{10}\). Dies ist ein erwünschter Überlauf!

Exercise 7.4 (Erwünschter und unerwünschter Überlauf.)

In welchen Fällen kann es zu einem unerwünschten Überlauf bei der Addition zweier \(n\)-Bit Binärzahlen kommen?

Solution to Exercise 7.4 (Erwünschter und unerwünschter Überlauf.)

Ein unerwünschter Überlauf kann nur dann eintreten wenn entweder beide Zahlen positive sind oder aber beide Zahlen negativ sind.

Die Subtraktion \(a - b\) zweier ganzer Zahlen \(a, b\) lässt sich auf die Addition \(a + (-b)\) zurückführen. Subtrahieren wir beispielsweise die Zahl \(00011_2 = 3_{10}\) von \(00111_2 = 7_{10}\) können wir das auf die Addition der Zahlen \(11101_2 = -3\) und \(00111_2 = 7_{10}\) zurückführen:

\[\begin{split} \begin{split} 11101_2&\\ +\ \ 00111_2&\\ \hline \hline \text{Übertrag:} \quad 111110_2&\\ \hline \hline = 100100_2& \end{split}\end{split}\]

Der erwünschte Überlauf entsteht und aus \(100100_2\) wird \(00100_2 = 4_{10}\).

Exercise 7.5 (Addition und Subtraktion von Binärzahlen)

Berechnen Sie das Ergebnis 4-Bit-Ergebnis folgender 4-Bit-Zahlen:

1. \(0101_2 + 1001_2\)

2. \(0111_2 + 0001_2\)

3. \(0011_2 + 0100_2\)

4. \(1100_2 + 0111_2\)

Solution to Exercise 7.5 (Addition und Subtraktion von Binärzahlen)

Die Addition dieser Zahlen ergibt:

1. \(0101_2 + 1001_2 = 1110_2 = -2_{10} = 5_{10} + (-7_{10})\)

2. \(0111_2 + 0001_2 = 1000_2 = -8_{10} = 7_{10} + 1_{10}\) (unerwünschter Übertrag)

3. \(0011_2 + 0100_2 = 0111_2 = 7_{10} = 3_{10} + 4_{10}\)

4. \(1100_2 + 0111_2 = 0011_2 = 3_{10} = -4_{10} + 7_{10}\) (erwünschter Übertrag)

7.3.3. Text

Wollen wir die Buchstaben des Alphabets in Binärdarstellung schreiben, so müssen wir uns darauf einigen welche Binärzahl welchen Buchstaben repräsentiert. Zum Beispiel könnten wir folgende Zuordnung verwenden:

Buchstabe	Dezimalzahl	Binärzahl
A	0	00000
B	1	00001
C	2	00010
D	3	00011
E	4	00100
…	…	…
Z	25	11001

Da in diesem Fall unsere Menge 26 Elemente enthält brauchen wir 26 Zustände und damit mindestens 5 Bits, denn es gilt

\[2^4 < 26 \leq 2^5.\]

Exercise 7.6 (Repräsentation)

Wie viele Bits benötigen Sie wenn Sie die Kleinbuchstaben auch repräsentieren möchten?

Solution to Exercise 7.6 (Repräsentation)

Mit Kleinbuchstaben haben wir \(52\) Elemente und brauche somit \(6\) Bits denn

\[2^5 < 52 \leq 2^6\]

Ein Wort besteht natürlich aus mehreren Buchstaben. Zum Beispiel wäre BAD repräsentiert durch \(00001 00000 00011\). Im Computer würden demnach 15 Lampen/Leitungen oder Transistoren, die entweder den Zustand Strom aus oder Strom an haben, das Wort repräsentieren.

Sonderzeichen wie Leerzeichen oder weitere Zeichen müssten wir in unsere Codierung noch einfügen. Auch könnten wir einen vollkommen anderen Zeichensatz benutzten. Programme die auf diesem aufbauen müssen die Codierung lediglich kennen.

Auch können wir längere Wörter oder ganze Sätze bilden, brauchen dafür natürlich Speicherplatz. In unserem Beispiel benötigt jeder Buchstabe 5 Bits. D. h., um einen Text mit, sagen wir 300 Zeichen im Speicher zu halten, brauchen wir die Bauteile für mindestens 1500 Bits was wiederum 187.5 Bytes bzw. 0.1875 kiloByte (kB) (\(10^3\) Byte) und ca. 0.1831 kibiByte (KB/KiB) (\(2^{10}\) Byte) sind.

7.3.4. Bilder

7.3.4.1. Rastergrafiken

Bilder, Videos und Grafiken in, z. B., Computerspielen, bestehen aus winzig kleinen quadratischen Pixeln. Jeder Pixel hat eine bestimmte Farbe. Wir nennen diese Grafiken auch Rastergrafiken. Farben werden wiederum durch Zahlen repräsentiert.

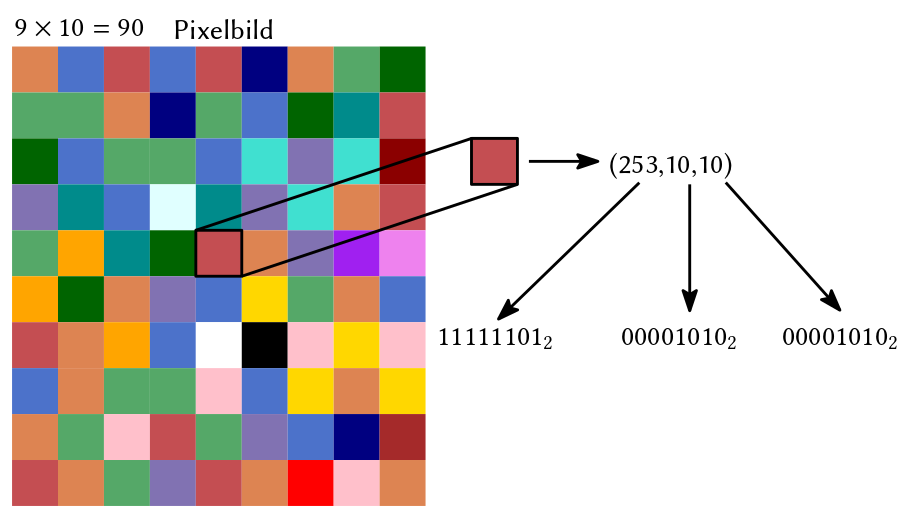
Abb. 7.4 Transformation eines Bildes in Bytes bzw. Bits.

Eine gängige Möglichkeit ist es eine Farbe durch den Anteil von Rot, Grün und Blau (RGB) zu definieren. Somit wird ein Pixel durch drei Zahlen repräsentiert und es ist üblich 256 Rot-, Blau- und Grün- Intensitäten zu verwenden. Damit lassen sich \(256^3\) unterschiedliche Farben repräsentieren. Zum Beispiel repräsentiert

\[(253, 10, 10)\]

einen sehr rötlichen Farbton. Für die 256 Intensitäten brauchen wir je 8 Bits, d.h. ein Byte.

Byte

\(8\) Bit ergeben ein Byte.

Byte

Oftmals ist ein Byte die kleinste Einheit auf die ein Computer zugreift.

Beispiel: Anstatt beispielsweise ein einzelnes Bit aus dem Speicher in die CPU zu laden, wird ein ganzes oder gar mehrere Bytes gelesen.

Pro Pixel benötigen wir demnach 3 Byte. Heute bestehen Bilder oft aus Millionen von Pixeln und ein gewöhnliches Video zeigt ca. 30 Bilder pro Sekunde. Damit wird klar, dass eine enorme Datenmenge entsteht und es verwundert nicht, dass Videos oftmals mehrere Gigabyte groß sind. Ist die Auflösung hoch, folgt daraus wiederum ein großer Energieverbrauch den die Video-Streamingdienste verursachen.

7.3.4.2. Vektorgrafiken

Eine weitere sehr interessante Technik ist es ein Bild durch einfache geometrische Objekte zu beschreiben. Zum Beispiel könnten wir ein Bild durch folgende Zeichenanweisungen repräsentieren:

Color(253,10,10)            # Wähle Pinsel mit Farbe (253,10,10)
Rectangle(0,0,100,100)      # Zeichne Rechteck
Line(1,1,99,99)             # Zeichne Linie

Was so viel bedeutet wie: Zeichne ein Rechteck von \((0,0)\) bis \((100,100)\) und eine Liniensegment, definiert durch die Punkte \((1,1)\) und \((99,99)\), in einer rötlichen Farbe.

Anstatt des „fertigen“ Bildes, speichern wir eine Vorschrift bzw. einen Algorithmus, der angibt wie dieses Bild gezeichnet wird. Diese Vorschrift wird in Binärcode umgewandelt und ein Programm, was solch eine Vorschrift lesen bzw. einen solchen Algorithmus ausführen kann, kümmert sich um die Umwandlung in eine Rastergrafik.

Diese Bilder sind sog. Vektorgrafiken. Der Vorteil der Vektorgrafik ist, dass die Beschreibung eine analoge/verlustfreie Beschreibung ist und die Digitalisierung (Verpixelung/Rasterisierung) des Bildes dynamisch, jedesmal wenn das Bild angezeigt wird, vollzogen wird. Dadurch ist es möglich die Schärfe des Bildes zu erhalten, selbst wenn Sie hineinzoomen. Man nennt diese Eigenschaft Auflösungsunabhängigkeit.

Exercise 7.7 (Vektor- vs. Rastergrafik)

Öffnen Sie ein PDF-Dokument oder eine SVG-Datei (ihr Browser kann diese in der Regel anzeigen) und zoomen Sie hinein. Öffnen Sie anschließend eine Rastergrafik, d.h. eine PNG-, JPEG-, GIF-, oder JPG-Datei und zoomen Sie hinein. Was beobachten Sie?

Solution to Exercise 7.7 (Vektor- vs. Rastergrafik)

Die Schrift im PDF-Dokument bleibt scharf. Bei einer Rastergrafik sehen wir ab einem bestimmten Zeitpunkt die einzelnen Pixel immer deutlicher.

Drucker können Vektorgrafiken oft besser darstellen, da sie ihre eigene optimale Auflösung verwenden können. Ein Nachteil der Technik ist, dass die Berechnung des Rasterbildes Rechenzeit und Speicher kostet und diese hängen nicht von der Größe des resultierenden Rasterbildes ab.

Das interessante an der Technik ist, dass wir für die persistente Speicherung Daten (die resultierenden Pixel) reduzieren und durch Rechenleistung ersetzen! Dieses Prinzip wird in der Informatik häufig verwendet. Ein Beispiel ist die Komprimierung oder Verschlüsselung von Daten.

Nehmen Sie ein sehr simples Beispiel der (verlustfreien) Komprimierung von Text: Nehmen wir an, wir hätten einen Text der aus der Folge von ab besteht also ababababab.... Sagen wir der Text ist \(200\) Zeichen lang und sagen wir jeder Buchstabe kostet uns \(1\) Byte Speicher. Dann können wir entweder alle \(200\) Zeichen speichern, was uns \(200\) Byte kostet, oder wir speichern einen Algorithmus der Form

'ab'*100

was uns 6 Byte kostet. Wir bräuchten dann ein Programm in Form eines Übersetzer, der die Anweisung 'ab'*100 versteht und ausführt. Wir verringern somit den verbrauchten Speicherplatz auf Kosten der Rechenzeit. Diese Technik ist eng mit dem Informationsbegriff verknüpft, siehe Informationstheorie.

7.3.5. Ton

Ton entsteht durch Vibration der Luft. Luft wird verdichtet und ausgedehnt, d.h. die Moleküldichte verändert sich. Diese Veränderung bewegt sich als Welle durch den Raum. Vergleichbar ist die Welle die entsteht wenn Sie einen Stein in einen See werfen. Die Energie bewegt sich durch das Medium bis an unser Ohr. Unser Ohr erkennt die oszillierende Druckveränderung (die Welle) und interpretiert diese als das was wir Ton nennen.

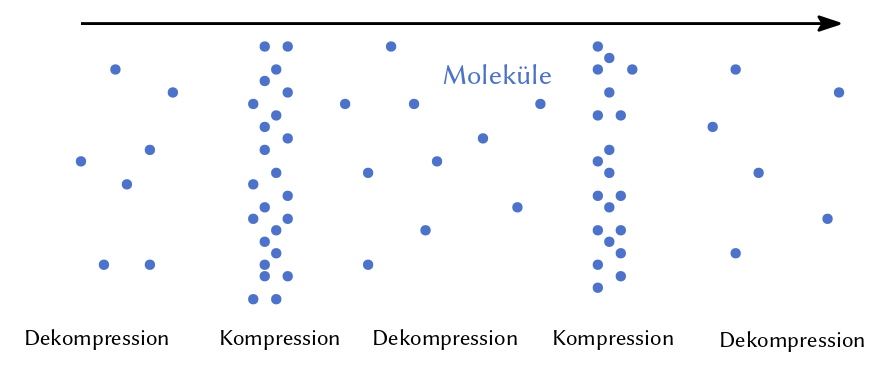
Abb. 7.5 Ein zyklischess Muster aus niedriger und hoher Moleküldichte, was mit der Zeit von links nach rechts wandert.

Die Oszillation lässt sich als periodische Funktion über die Zeit darstellen. Ton kann durch eine Funktion \(f(t)\) der Amplitude (Lautstärke) über die Zeit \(t\) dargestellt werden. Lautsprecher wandeln die Funktion wiederum in Druckveränderungen der Luft um, sodass unser Ohr die Funktion wahrnehmen kann. Die Frequenz der Oszillation, d.h. wie schnell das Wechselspiel von Kompression und Dekompression vonstattengeht, bestimmt die Tonhöhe.

Wir können keine solche (reelle) Funktion mit lediglich zwei Zuständen, d.h. Strom aus und Strom an repräsentieren, da diese unendlich viele Werte annimmt. Wir können von der Funktion aber eine sogenannte Stichprobe (engl. Sample) erstellen. Dazu werten wir die Funktion an endlich vielen Stellen \(t = t_0, \ldots, t_n\) aus und speichern die zugehörigen Werte \(\hat{f}(t_0), \ldots, \hat{f}(t_n)\) ab. Dabei ist \(\hat{f}(t_i)\) eine Annäherung des eigentlichen Funktionswerts, d.h. \(\hat{f}(t_i) \approx f(t_i)\). Je mehr Samples wir pro Sekunde machen und je genauer wir die Amplitude an den Samplepunkten treffen, desto genauer wird unsere Annäherung an \(f(t)\).

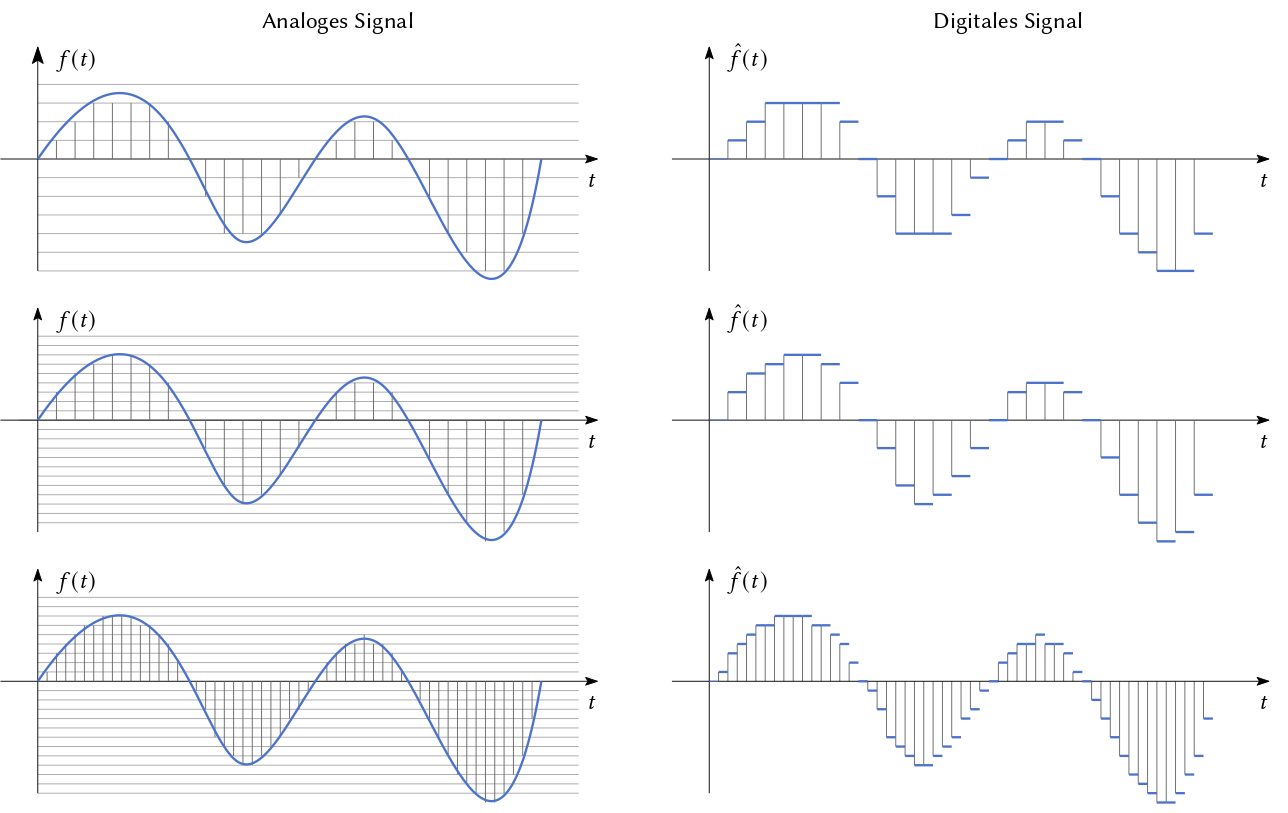
Abb. 7.6 Transformation des analogen Tons in digitale Samples. Links das analoge Signal und rechts die Samples. Erst erhöhen wir die Bit-Tiefe (zweite Zeile), dann die Sample-Rate (dritte Zeile).

Ton wird als Folge von Zahlen repräsentiert. Diese Folge transformieren Lautsprecher in Vibration und damit in Ton. Gewöhnlich verwendet man eine sog. Sample-Rate (Stichproben-Rate) von 44.1 kHz, d.h. 44100 Stichproben pro Sekunde. Der Wert der Amplitude \(\hat{f}(t_i)\), in Form einer Fließkommazahl/Gleitkommazahl, wird heute normalerweise durch 32 Bits also 4 Byte durch repräsentiert.

Exercise 7.8 (Speicherplatz)

Wie viel Speicherplatz verbraucht ein (unkomprimierter) 3-Minuten-Song der in einer Sample-Rate von 44.1 kHz und einer Bit-Tiefe von 32 Bits abgespeichert wurde?

Solution to Exercise 7.8 (Speicherplatz)

Bei \(44100\) Samplepunkte pro Sekunde, wobei jeder Punkt 32 Bits kostet, brauchen wir insgesamt

\[44100 \cdot 60 \cdot 3 \cdot 32 = 32.752\]

Megabyte also ca. \(33\) MB, was \(33 \cdot 10^6 \cdot 8\) Bits sind.

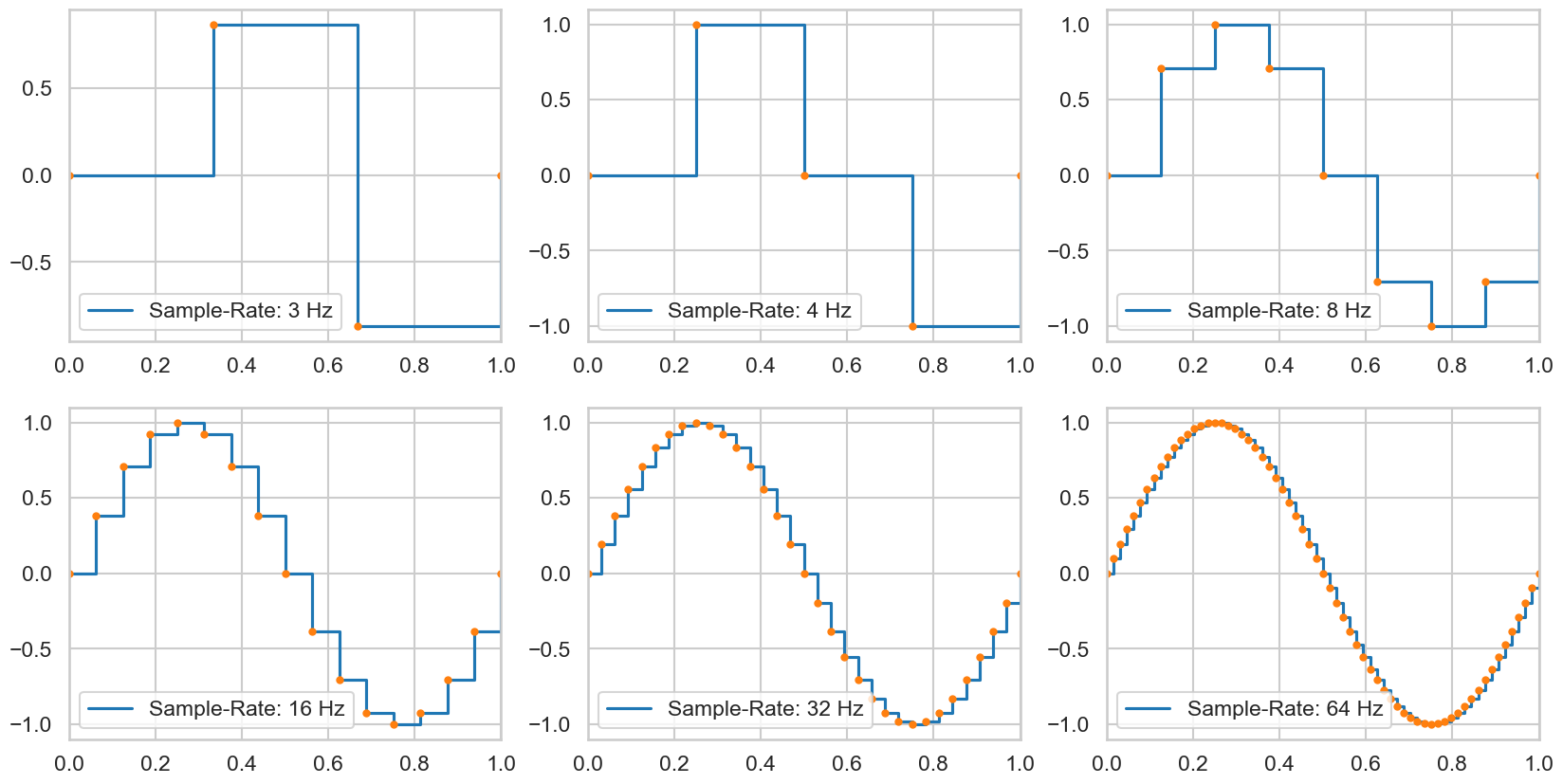
Folgender Python-Code erzeugt und plottet Samples einer Sinuswelle mit der Frequenz von \(1\) Hz über den Zeitraum von einer Sekunde. Es wird eine Sample-Rate von 3, 4, 8, 16, 32 und 64 Hz verwendet. Auch hier gilt: Sie brauchen den Code noch nicht verstehen aber vielleicht möchten Sie zu einem späteren Zeitpunkt analysieren was hier geschieht.

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

sns.set_style("whitegrid")
sns.set_context("talk")

def sine_wave(freq=200, amp=1):
    return lambda x : np.sin(freq * 2 * np.pi * x)

def sample(f, sample_rate=441000, dt=10):
    steps = 1.0/sample_rate   # Sample-Punkte von Sekunde 0 bis sekunde Sekunden dt
    t = np.arange(0,dt,steps) # in 1/sample_rate schritten
    y = f(t)                  # f(t) für alle Sample-Punkte
    t = np.append(t, [1.0])
    y = np.append(y, [f(1.0)])
    return t, y

# Sinus-Welle mit der Frequenz von 1 Hz und der Amplitude 1
f = sine_wave(freq=1.0, amp=1.0)

# Verschiedene Samples, erzeugt durch verschiedene Sample-Rates
#plt.rcParams['font.size'] = '16'
fig, axs = plt.subplots(2, 3, figsize=(20,10))
i = 0
j = 0
for sample_rate in [3,4,8,16,32,64]:
    #fig.suptitle('Samples der Sinueswelle $\\sin(2\\pi \\cdot t$) über eien Zeitraum von 1 Sekunde')
    t, y = sample(f, sample_rate=sample_rate, dt=1)
    axs[i][j].step(t, y, where='post', label=f'Sample-Rate: {sample_rate} Hz')
    axs[i][j].plot(t, y, marker='o', ms=5, linewidth=0)
    axs[i][j].set_xlim([0,1])
    axs[i][j].legend()
    if(j < 2):
        j += 1
    else:
        j = 0
        i += 1
plt.show()

Exercise 7.9 (Daten vs. Algorithmen)

Nehmen wir an Sie möchten den Ton einer einfachen \(200\) Herz Sinuswelle

\[f(t) = \sin(200 \cdot 2\pi \cdot t),\]

der sich über den Zeitraum von \(10\) Sekunden erstreckt, speichern. Wie könnten Sie diesen Ton durch extrem wenig Speicherplatz abspeichern? Oder anders gefragt: Durch was lässt sich diese Funktion repräsentieren? Tipp: Denken Sie an die Vektorgrafik.

Solution to Exercise 7.9 (Daten vs. Algorithmen)

Anstatt zu sampeln speichern wir die Funktionsbeschreibung und den Zeitraum. Zum Beispiel könnten wir die Frequenz, also \(200\) Hz, und die \(10\) Sekunden abspeichern. Das kostet uns nur wenige Bits.