10.1. Algorithmen

Der Ursprungs des Begriffs Algorithmus war lange Zeit ungeklärt. Erst recht spät fanden Historiker*innen heraus, dass der Begriff von der leichten Veränderung des Namens des berühmten persischen Autors Abu Dschaʿfar Muhammad ibn Musa al-Chwārizmī stammt. Der Begriff wurde dann durch Algorismi latinisiert und durch Algorismus ins mittelhochdeutsch übersetzt. Vor nicht allzu langer Zeit wurde das Wort mit dem griechischen Begriff Arithmetik verknüpft und so entstand schließlich der Name Algorithmus.

Lange Zeit verstand man darunter die Kombination aus arithmetischen Operationen (Addition, Subtraktion, Multiplikation und Division). Um 1950 herum deutete der Begriff auf Euklid’s berühmten Algorithmus zum finden des größten gemeinsamen Teilers. Das heißt, ab dieser Zeit verblasste die Vorstellung von der Kombination rein arithmetischer Operationen. Algorithmen begannen kombinatorische Operationen und Kontrollstrukturen zu enthalten.

Heute verbinden wir mit Algorithmus Begriffe wie Rezept, Berechnungsvorschrift, Prozess, Prozedur, Methode, Routine und so weiter.

10.1.1. Euklidischer Algorithmus

Lassen Sie uns den ersten aller noch heute relevanten Algorithmen betrachten: Den Euklidischen Algorithmus.

Exercise 10.1 (Euklidischer Algorithmus)

Gegeben seien zwei natürliche Zahlen \(n, m \in \mathbb{N}\). Wir suchen nach dem größten gemeinsamen Teiler \(\text{ggT}(n,m)\) von \(n\) und \(m\), d.h., die größte natürliche Zahl die sowohl \(n\) als auch \(m\) teilt.

Der \(\text{ggT}(44,12)\) von \(44\) und \(12\) ist zum Beispiel \(4\). Wie vieles bei den Griechen ist der Algorithmus geometrisch motiviert. Euklid berechnet den ggT, indem er nach einem gemeinsamen „Maß“ für die Längen zweier Linien sucht. Dazu zieht er wiederholt die kleiner der beiden Längen von der größeren ab. Der ggT verändert sich dadurch nicht.

Gesetzt des größter gemeinsamer Teiler

Seien \(n\), \(m\) zwei natürliche Zahlen mit \(n > m\) und \(d = n - m\), so ist der größte gemeinsame Teiler von \(n\), \(m\) und \(d\) identisch.

Beweis

Jede natürliche Zahl kann als Produkt ihrer Primfaktorzerlegung geschrieben werden. Der \(\text{ggT}(n,m)\) ergibt sich aus der Multiplikation aller Primzahlen die in beiden Zerlegungen (möglicherweise mehrfach) vorkommen.

Zum Beispiel ist: \(44 = (2 \cdot 2) \cdot 11\) und \(12 = (2 \cdot 2) \cdot 3\) und ihr \(\text{ggT}(44,12) = 2 \cdot 2\).

Seien nun

\[n = p_1 \cdot \ldots \cdot p_k \cdot q_1\]

und

\[m = p_1 \cdot \ldots \cdot p_k \cdot q_2,\]

wobei \(p_1, \ldots, p_k\) die \(k\) gleichen Primzahlen der Zerlegungen sind. Dann folgt

\[d = n - m = (p_1 \cdot \ldots \cdot p_k) \cdot (q_1 - q_2)\]

und somit gilt

\[\text{ggT}(n,m) = \text{ggT}(d,m) = \text{ggT}(n,d) = (p_1 \cdot \ldots \cdot p_k).\]

10.1.1.1. Version 1

Aus dem Gesetzt des größter gemeinsamer Teiler, folgt der euklidische Algorithmus. Wir starten mit zwei Zahlen, und ziehen solange immer und immer wieder die kleinere von der größeren ab, bis beide Zahlen gleich sind. Das Ergebnis ist der größter gemeinsamer Teiler der beiden ursprünglichen Zahlen!

Gehen wir wie Euklid vor und beschreiben diese Vorgehensweise in Pseudocode:

n <- c0
m <- c1
Solange m ungleich n:
  n <- n - m
  Falls m > n:
    t <- m
    m <- n
    n <- t

Dabei sind c0 und c1 irgendwelche natürliche Zahlen wobei c0 größer gleich c1 sein muss. Überführen wir diesen Code in ein Python-Programm um. Durch die Restwertdivision können m nicht n teilt in Python realisieren:

def gcd(n,m):
    while n != m: # Solange m ungleich n
        n = n - m
        if m > n:
          t = m
          m = n
          n = t
    return m

gcd(544, 119)

17

Die Funktion gcd hat zwei Parameter n und m die mit den Argumenten 544 und 119 initialisiert werden. Implizit wird angenommen, dass n > m gilt. Nachdem die while-Schleife (Wiederholung) verlassen wird, gibt die Funktion m zurück.

Zuweisungen werden in den allermeisten Programmiersprachen anstatt mit <- mit dem = durchgeführt (siehe auch Abschnitt Initialisierung und Zuweisung). Das mathematische \(=\) wird aufgrund dessen mit == ausgedrückt.

10.1.1.2. Version 2

Da uns die Restwertdivision als Operation zur Verfügung steht, können wir die wiederholte Subtraktion beschleunigen. Anstatt zum Beispiel 43 - 11 - 11 - 11 == 10 zu rechnen ergibt 43 % 11 == 10. Diese Operation steht Ihnen in allen gängigen Programmiersprachen zur Verfügung und kann auf dem Computer sehr schnell ausgeführt werden.

Dadurch vereinfacht sich der euklidische Algorithmus zu:

n <- c0
m <- c1
Solange m > 0:
    r <- n % m
    n <- m
    m <- r

Die Anweisungen werden von oben nach unten ausgeführt, wobei Solange eine Wiederholung markiert. Alles was unter dieser Anweisung eingerückt steht, wird wiederholt, solange die Bedingung m > 0 gilt. Nach diesen Schritten ist der Wert auf den die Variable n verweist, der größten gemeinsamen Teiler (ggT) von c0 und c1. Die Operation n % m berechnet den Rest der Restwertdivision. Unter r <- n % m verstehen wir die Zuweisung des Wertes n % m zur Variablen r.

Um einen Algorithmus zu verstehen hilft es oft ihn auszuführen. Wir möchten den ggT von \(544\) und \(119\) bestimmen. Wir beginnen mit

1. \(n \leftarrow 544\)

2. \(m \leftarrow 119\).

Wir treten in die Wiederholung ein, da \(m > 0\) gilt. Es ergibt sich:

1. \(r \leftarrow 68\)

2. \(n \leftarrow 119\)

3. \(m \leftarrow 68\)

Erneut treten wir in die Wiederholung ein, da weiterhin \(m > 0\) gilt. Es ergibt sich:

1. \(r \leftarrow 51\)

2. \(n \leftarrow 68\)

3. \(m \leftarrow 51\)

Erneut treten wir in die Wiederholung ein, da weiterhin \(m > 0\) gilt. Es ergibt sich:

1. \(r \leftarrow 17\)

2. \(n \leftarrow 51\)

3. \(m \leftarrow 17\)

Erneut treten wir in die Wiederholung ein, da weiterhin \(m > 0\) gilt. Es ergibt sich:

1. \(r \leftarrow 0\)

2. \(n \leftarrow 17\)

3. \(m \leftarrow 0\)

Da nun \(m\) den Wert \(0\) hat, verlassen wir die Wiederholung und das Ergebnis steht in \(n\).

Lassen Sie uns den Algorithmus in reneut in ein Python-Programm überführen:

def gcd(n,m):
    while m > 0:
        r = n % m
        n = m
        m = r
    return n

gcd(544, 119)

17

Die Funktion gcd hat zwei Parameter n und m die mit den Argumenten 544 und 119 initialisiert werden. Nachdem die while-Schleife (Wiederholung) verlassen wird, gibt die Funktion n zurück.

10.1.1.3. Version 3

In Python können wir das Vertauschen der Variablen durch Tupel und das sog. Packing/Unpacking kürzer schreiben. Auch ist die Bedingung einer while-Schleife wahr sofern eine ganze Zahl nicht gleich 0 ist. Daraus ergibt sich die sehr kurze Version 3:

def gcd(a,b):
    while b:
        a, b = b, a % b
    return a

gcd(544, 119)

17

Alle drei Versionen berechnen den ggT, also den gleichen Wert. Version 1 und 2 unterscheiden sich semantisch wohingegen Version 2 und 3 sich lediglich syntaktisch unterscheiden. Das sind also Algorithmen.

Was zeichnet nun aber einen Algorithmus genau aus?

10.1.2. Definition

Nach dieser Intuition wollen wir den Begriff Algorithmus klar definieren. Dabei bedienen wir uns bei Donald E. Knuth, dem Autor der Programmierbibel The Art of Programming und Urheber des Textsatzsystems TeX.

Algorithmus (informell)

Ein Algorithmus ist eine endliche Folge von unmissverständlich beschriebenen ausführbaren Anweisung (z.B. Text/Programmcode), um für eine bestimmte endliche Eingabe in endlich vielen Schritten eine endliche Ausgabe zu erzeugen, wobei zu jeder Zeit der Ausführung nur endlich viel Speicherplatz verwendet wird.

Ein Algorithmus hat demnach folgende Eigenschaften:

(1) Endlichkeit:

Identisch zur Beschreibung einer Turingmaschine, besteht ein Algorithmus aus endlich vielen Zeichen. Anders ausgedrückt, können wir ihn in endlich viel Zeit niederschreiben. Durch die Endlichkeit seiner Beschreibung, kann ein Algorithmus als Programm in einem (endlichen) Speicher abgelegt werden.

(2) Ausführbarkeit:

Jede Anweisung des Algorithmus muss ausführbar sein. Das heißt, die Semantik einer jeden Anweisung muss im jeweiligen Kontext eindeutig definiert sein. Es muss in jedem Schritt nicht nur klar sein was zu tun ist, sondern dieses was muss auch tatsächlich möglich sein.

(3) Gebundenheit:

Während der Ausführung des Algorithmus wird lediglich endlich viel Speicher bzw. eine endliche Anzahl an Variablen benötigt.

(4) Terminierung:

Die Ausführung eines Algorithmus muss nach endlich vielen Schritten enden. Die Terminierung ist das Gegenstück zur Gebundenheit bezogen auf die Zeit. (1) und (4) stellen sicher, dass ein Programm und dessen Ressourcen zusammengenommen nur endlich viel Speicher verbrauchen. In der Komplexitätstheorie spricht man hierbei von dynamischer Finitheit des Speicherbedarfs.

(5) Eingabe:

Jeder Algorithmus hat entweder keine oder eine endliche Eingabe.

(6) Ausgabe:

Jeder Algorithmus liefert mindestens eine Ausgabe, d.h., ein Ergebnis zurück.

Es gibt noch zwei optionale Eigenschaften für Algorithmen, welche oftmals gefordert werden:

(7) Determiniertheit:

Wir nennen einen Algorithmus determiniert, wenn er bei gleicher Eingabe auch die gleiche Ausgabe erzeugt. Entscheidet ein Algorithmus durch einen echten Münzwurf (kein pseudo Zufall sondern echter Zufall) über den Verlauf der Ausführung, so wäre jener Algorithmus nicht determiniert. Algorithmen basieren wenn überhaupt auf Pseudozufallszahlen, deren Erzeugung mit einem Startwert (Seed) initialisiert wird. Bei gleichem Seed und gleicher Eingabe erzeugen diese Algorithmen auch das gleiche Ergebnis. Da der Seed zur Eingabe gehört, sind jene Algorithmen determiniert.

(8) Determinismus:

Wir nennen einen Algorithmus deterministisch, wenn dieser während seiner Ausführung zu jedem Zeitpunkt die nächste Anweisung eindeutig definiert. Es gibt keine reale digitale Maschine die nichtdeterministische Algorithmen direkt umsetzten kann. Ein Beispiel für einen nichtdeterministischen Algorithmus wäre die Wanderung durch ein Labyrinth wobei Sie bei jeder Verzweigung beide Wege zeitgleich ablaufen. Dies ist nicht möglich, da Sie sich klonen müssten bzw. an zwei Orten gleichzeitig sein müssten. Verwechseln Sie dies nicht mit der Parallelität. Es ist natürlich möglich, dass sich zwei Personen bei einer Abzweigung trennen. Nichtdeterminismus bedarf jedoch der Kopie des gesamten Zustands der Maschine!

Determinismus und Determiniertheit hängen zusammen, denn Determiniertheit folgt aus dem Determinismus jedoch folgt aus der Determiniertheit nicht unbedingt der Determinismus.

Algorithmus (formal)

Eine Berechnungsvorschrift ist genau dann ein Algorithmus, wenn eine zu dieser Berechnungsvorschrift äquivalente Turingmaschine \(T\) existiert, die für jede Eingabe \(w\) stoppt und die gleiche Ausgabe wie die Berechnungsvorschrift liefert.

Im Abschnitt Berechenbarkeit haben wir bereits erwähnt, dass das Halteproblem nicht berechenbar ist. D.h., es gibt keine Turingmaschine/Algorithmus die/der für beliebige Turingmaschinen/Algorithmen prüfen kann, ob diese terminieren. Die Terminierung ist damit im Einzelfall zu prüfen.

10.1.3. Das Was und das Wie

Nach unserer Auffassung muss ein Algorithmus nicht zwangsläufig von einer Maschine verstanden werden. Die Unmissverständlichkeit bezieht sich hingegen auf einen bestimmten Kontext und im Falle der von Maschinen ausgeführten Algorithmen, gehört die Maschine zu diesem Kontext. So ist ein Kochrezept ein Algorithmus der im Kontext der Küche und des Kochens eine (hoffentlich) unmissverständliche endliche Folge von Anweisungen darstellt. Durch das Ausführen des Kochrezepts können wir mithilfe von bestimmten Kochutensilien (Eingabe) ein bestimmtes Gericht (Ausgabe) zubereiten.

Algorithmen lassen sich auch von der ausführenden Einheit, also der Maschine oder dem Koch / der Köchin loslösen. Während des Entwickelns eines Algorithmus sollte uns immer klar sein, was eine bestimmte Anweisung berechnet, d.h., was passiert, doch kann es unklar sein wie dies realisiert wird. In der Realwelt sind wir daran gewöhnt. Wir wissen zwar dass uns der Flieger von München nach Frankfurt bringt, wie das aber im Detail funktioniert ist nicht bekannt. Selbst bei den einfachsten Dingen des Alltags wissen wir sehr oft nicht wie die Dinge genau funktionieren. Bevor wir uns Gedanken über Hammer und Nagel machen, hauen wir den Hammer in die Wand.

Ein Beispiel aus der Programmierung wäre folgendes: Nehmen wir an min liefert uns die kleinste und max die größte Zahl aus einer Liste von Zahlen. Wir kennen also das Was. Wie min und max dies realisieren bleibt im folgenden Algorithmus verborgen und selbstverständlich können wir min bzw. max verwenden ohne das Wie zu kennen.

x = [1, 36, 8, 3, 41, -123, 0, 3]
x_min = min(x)
x_max = max(x)
print(x_min)
print(x_max)

-123
41

Dies ist die Norm. Ihre Algorithmen werden unmissverständlich sein, was jedoch im Detail auf der ausführenden Einheit passiert, bleibt verborgen. Je nachdem welche Programmiersprache und welche Bibliotheken/Pakete Sie verwenden, befinden Sie sich näher oder weiter weg von der ausführenden Einheit. Zusätzlich können Sie sich selbst weiter von ihr entfernen. Zum Beispiel können wir eine Funktion schreiben, die uns das größte und kleinste Element einer Liste zurückliefert:

def min_and_max(l):
    l_min = min(x)
    l_max = max(x)
    return l_min, l_max

x = [1, 36, 8, 3, 41, -123, 0, 3]
print(min_and_max(x))

(-123, 41)

Obwohl wir das Wie von min und max womöglich nicht kennen, wissen wir dass min_and_max funktioniert, da wir das Was von min und max kennen.

Je maschinennäher Sie programmieren, desto mehr Kontrolle aber auch Verantwortung haben Sie über die genaue Umsetzung (das Wie). Doch wie wir alle wissen:

With great power comes great responsibility.

Diese zusätzliche Kontrolle können Sie nicht einfach abgeben. Sie führt gewöhnlich zu einem höheren Entwicklungsaufwand.

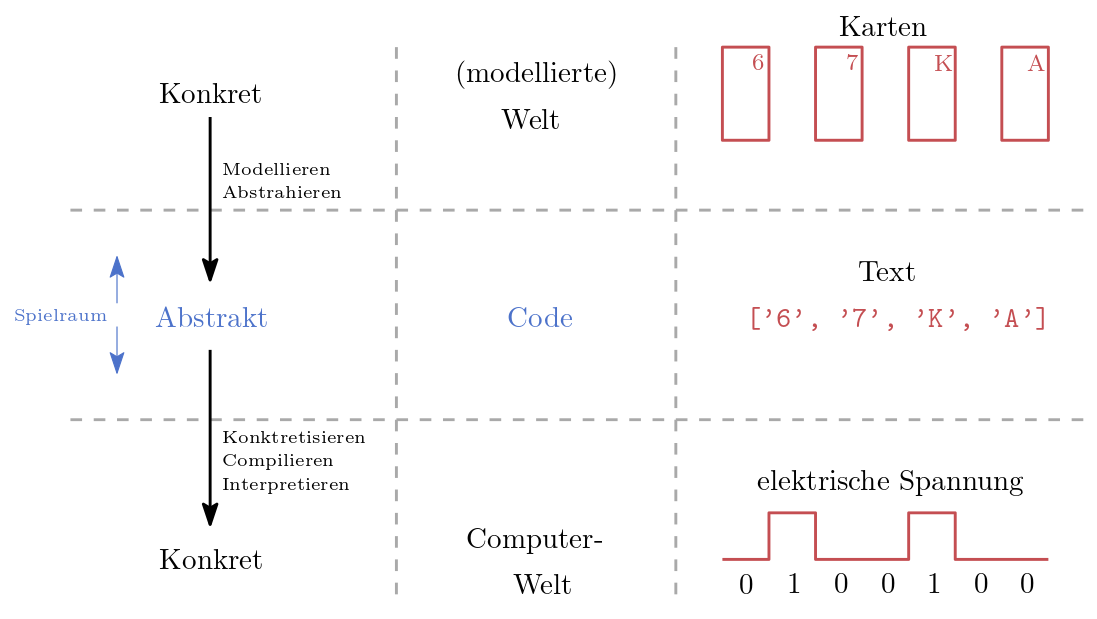
Abb. 10.1 Zusammenhang zwischen modellierter Welt, Quellcode und der realen Welt der Computer.

Je näher Sie an der Maschine programmieren, desto näher befinden Sie sich in der wirklichen physikalischen Welt der Transistoren und elektrischen Schaltkreise. Paradoxerweise führt die Nähe zur wirklichen Welt dazu, dass es schwerer wird die wirkliche Welt zu modellieren. Wir sprechen hier von zwei verschiedenen Welten, der Welt der elektrischen Schaltkreise und beispielsweise der Welt der Planeten oder die Welt des Kartensortierens. Programmiersprachen katapultieren uns in eine abstrakte Welt mit der wir eine konkrete Welt modellieren können. Das Modell wird durch die konkrete Computerwelt schlussendlich berechnet. Vergleichen Sie hierzu die Abbildung 10.1. Als Computational Thinker*innen halten wir uns meist zwischen der Welt die wir modellieren wollen und der abstrakten Welt (Code) auf.

Wie wir uns von der Maschine wegbewegen und so an Abstraktheit gewinnen, hat wiederum mit der von uns bereits diskutierten Interpretation \(I\) zu tun. Die oben beschriebene Funktion min_and_max führt zu einer neuen Interpretation in welcher min_and_max ein Repräsentant ist. Dieser repräsentiert alle notwendigen Anweisungen für die Berechnung und Rückgabe des maximalen und minimalen Elements einer Liste. min, max return l_min, l_max können wir als Bedeutungen dieser Interpretation ansehen. Gleichzeitig sind diese Anweisungen wiederum Repräsentanten einer weiteren Interpretation, welche ins Konkretere führt.

Sogenannte Hochsprachen wie Python, Java, C# abstrahieren die Welt der elektrischen Schaltkreise in eine phantastische Welt aus Datenstrukturen, Variablen, Funktionen, Klassen und Objekte. Pakete und Bibliotheken reichern diese Welt mit weiteren Algorithmen und Datenstrukturen an. Diese Pakete und Bibliotheken werden unentwegt von Programmierer*innen durch Computational Thinking erschaffen. Durch die Abstraktion wird es möglich, dass elektrische Schaltkreise ganze Galaxien simulieren, Fahrzeuge bewegen oder Transaktionen durchführen. Schlussendlich basiert jedoch alles auf zwei Zuständen, 0 und 1, unvorstellbar vieler winziger elektrischer Bauteile.

10.1.4. Die Natur eines Algorithmus

Lassen Sie uns noch ein wenig tiefer in die Natur eines Algorithmus einsteigen. Achtung! Es wird ein wenig philosophisch.

Überlegen Sie sich einmal was die Zahl \(2\) eigentlich ist? Zunächst einmal ist sie ein Zeichen was wir soeben niedergeschrieben haben. Doch angenommen vor Ihnen lägen zwei Äpfel. In diesem Fall wird die \(2\) durch diese zwei Äpfel ausgedrückt. Wir finden Formen der \(2\) an vielen verschiedenen Orten in der realen Welt aber nirgends finden wir DIE eine einzigartige \(2\).

Was DIE \(2\) wirklich ist, ist ein Problem mit dem sich viele Philosophen schon auseinander gesetzt haben. Platon ging davon aus, dass es eine echte Welt der Ideen gäbe, in der die Idee der \(2\) enthalten ist. Nach seiner Vorstellung tragen alle Repräsentanten der \(2\) die Idee der \(2\) in sich. Die Idee der \(2\) scheint durch den Repräsentanten hindurch. Vertreter dieser Strömung (z.b. Gottlob Frege, Kurt Gödel, Hilary Putnam, Penelope Maddy) werden als mathematische Platonisten bezeichnet.

Nominalisten (z.B. Ludwig Wittgenstein, Rudolf Carnap, Harty Field) lehnen diese Ideenwelt ab und definieren die \(2\) als Objekt in Raum und Zeit, welches ein Repräsentant aller zwei realen Objekte ist. So gesehen würde die \(2\) aus unserer Welt verschwinden sobald es keine Repräsentanten von ihr mehr gäbe.

Das ist ja alles schön und gut aber was hat das mit den Algorithmen zu tun? Ein Algorithmus kann auch als ein Repräsentant (oder als eine Idee der Ideenwelt) aufgefasst werden. Der euklidische Algorithmus zum Finden des größten gemeinsamen Teilers gcd, kann in vielen Unterschiedlichen Formen niedergeschrieben werden. Wie oben bereits beobachtet, kann es unterschiedliche Versionen, d.h., unterschiedliche Algorithmen geben, die genau das gleiche berechnen. Der Algorithmus kann sogar nur in unserem Kopf existieren. Ist der gcd in Java ein anderer Algorithmus als der in Python? Ändere ich die Namen meiner Variablen, ist es dann ein anderer Algorithmus? Darüber lässt sich streiten. Sicher können wir zwei Versionen auf syntaktische und semantische Unterschiede vergleichen.

Unterschiedliche Algorithmen

Unterscheiden sich zwei Beschreibungen eines Algorithmus semantisch, sprechen wir von zwei verschiedenen Algorithmen. Sind die beiden Beschreibungen semantisch identisch, dann handelt es sich auch um den gleichen Algorithmus.

Wir sagen aber gewöhnlich:

Ich habe den gcd-Algorithmus in Python programmiert

oder

Das ist der Pseudocode für den gcd-Algorithmus.

Und damit meinen wir in der Regel einen von vielen effizienten Algorithmen, welche allesamt den ggT berechnen.

Ob nun ein Algorithmus ein Repräsentant all seiner Realisierungen ist oder ob jede Realisierung ein eigener Algorithmus ist, ist in der Praxis unwichtig. Dennoch lohnt es sich ein paar Gehirnzellen dieser Fragestellung zu widmen. Beantworten Sie es für sich selbst.