22. Binäres Zeichnen#

Lernziel

In diesem Abschnitt werden wir das was wir im Abschnitt Interpretation und Repräsentation besprochen hatten konkretisieren. Wir werden eine bestimmte Interpretation nutzten um aus einer Folge von 0 und 1 Bilder

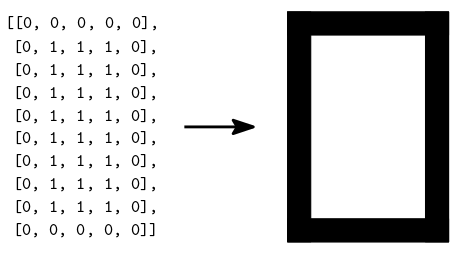
../../_images/zero-and-one-to-bw-picture.png

und Animationen zu generieren.

../../_images/flower.gif

Sie werden lernen wie Informationen erst durch einen Interpreter eine bestimmte Bedeutung erlangen. Sie werden den Umgang mit mehrdimensionalen Python-Listen und Tupeln erlernen. Außerdem werden Sie durch die Konstruktion einer eignen Interpretation in eine abstraktere Welt gelangen und sich in dieser austoben. Im Zuge dessen werden Sie Probleme in viele Teilprobleme aufteilen (Dekomposition). Sie werden Ihre Mustererkennung benötigen und auch mathematisches Denken praktizieren.

22.1. Interpretation#

Wir beginnen mit einem Schwarz-Weiß-Rasterbild. In anderen Worten: Lassen Sie uns unsere eigene Interpretation konstruieren.

Wir orientieren uns an dem sog. Rasterbild. Es hat eine bestimmte Anzahl an Pixel in \(x\) und \(y\)-Richtung. Die Anzahl \(n\) in \(x\)-Richtung bezeichnen wir als Spalten und die Anzahl \(m\) in \(y\)-Richtung bezeichnen wir als Zeilen. Wir wollen lediglich Schwarz-Weiß-Bilder zeichnen können, deshalb benötigen wir nur zwei mögliche Zustände je Pixel. Wir modellieren dies mit 0 (schwarz) und 1 (weiß). Das Bild kann als \(m \times n\)-Matrix \(B\) mit \(B \in \mathbb{B}^{m \times n}\) aufgefasst werden.

Exercise 22.1 (Bits pro Pixel)

Wie viele Bits benötigen Sie für jeden Pixel?

Jede Zeile des Bildes repräsentieren wir als Folge von 0 und 1. Da wir unser Bild verändern möchten, eignet sich in Python hierfür die Liste list.

row = [0, 1, 0, 1, 0, 1, 1]

Ein Bild modellieren wir wiederum als Liste von Zeilen (Pixelstreifen) oder eben eine Liste von Listen.

picture = [[0, 1, 0, 1, 0, 1, 1], # 1. Zeile
           [1, 1, 0, 1, 0, 1, 1], # 2. Zeile
           [0, 0, 1, 1, 1, 1, 1], # 3. Zeile
           [1, 0, 0, 1, 0, 1, 1]] # 4. Zeile

Unsere Interpretation erhält als Argument, d.h., als Repräsentanten eine zweidimensionale Liste aus Binärzahlen und liefert ein Schwarz-Weiß-Bild. Den notwendigen Interpreter, der diese Interpretation realisiert, bietet uns folgende Funktion:

import matplotlib.pyplot as plt
def plot_picture(picture):
    plt.imshow(picture, cmap='gray', vmin=0, vmax=1)

plot_picture(picture)
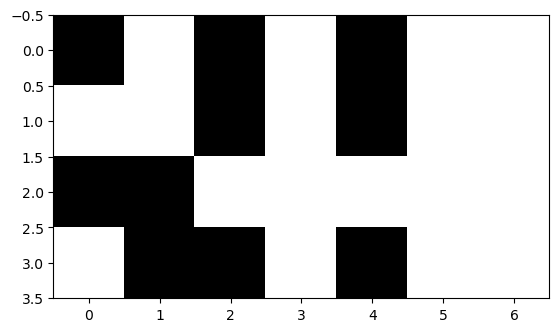
../../_images/fce4f8033e91cd22a3eff3234434810679e3d22efc3ee8b2a8369df9ddcf8c77.png

Wir haben nun alles was wir brauchen um richtig loszulegen: Eine Interpretation in Form einer Liste von Listen und einen Interpreter in Form der Funktion plot_picture.

22.1.1. Listen in Python#

Bevor wir weiter fortfahren, lassen Sie uns einen wiederholten Blick auf die Python-Liste werfen. Eine ausführlichere Diskussion zu Listen finden Sie im Abschnitt Listen im Teil PYTHON.

Der Zugriff auf einzelne Listenelemente einer zweidimensionalen Liste unterscheidet sich im Endeffekt nicht von dem der eindimensionalen Liste. Mit

picture[3][5]

1

greifen wir auf die vierte Liste der Liste picture zu und in dieser auf das sechste Element. Bedenken Sie, dass der Index einer Liste mit 0 startet. Im Falle unseres Bildes entspricht dies dem Zugriff des sechsten Elements in der vierten Zeile.

Wenn Sie mit Listen arbeiten, ist es wichtig zu wissen wie diese im Speicher abgelegt werden, siehe Abschnitt Listen und der Speicher. Wenn wir unser Rasterbild aus Listen von Listen konstruieren müssen wir dieses Wissen mit einbeziehen. Folgender Code erzeugt ein Bild mit zwei identischen Zeilen zu erzeugen.

row = [0, 1, 0, 1, 0, 1, 1]
picture = [row, row]

Da die beiden Zeilen identische sind, entsteht ein merkwürdiges Phänomen, welches die folgende Aufgabe zum Vorschein bringt.

Exercise 22.2 (Kopie einer Liste)

Ändern Sie einen einzelnen Pixel des eben konstruierten Bildes picture und lassen Sie sich das Ergebnis anzeigen. Was stellen Sie fest?

Unser Bild enthält nicht nur zwei gleiche sondern zwei identische Zeilen. Die Zeile, also der Wert [0, 1, 0, 1, 0, 1, 1] wird nicht kopiert. Stattdessen wird die Speicheradresse kopiert, sodass beide Einträge der Liste picture die gleiche Adresse enthalten:

print(f'Address of first row is {id(picture[0])}')
print(f'Address of second row is {id(picture[1])}')

Address of first row is 4474322304
Address of second row is 4474322304

Um das gewünschte Ergebnis zu erzielen, müssen wir den Wert der Liste row und nicht deren Adresse kopieren. In anderen Worten: Wir müssen eine tiefe und keine flache Kopie anlegen, siehe Abschnitt Tiefe und flache Kopie. Hierzu bietet uns Python die Listen-Methode copy() an:

row = [0, 1, 0, 1, 0, 1, 1]
picture = [row.copy(), row.copy()]

Da nun alle Listenelemente in row kopiert werden, können Sie sicher sein, dass Änderungen der Listenelemente nur jene eine Liste betreffen. Bedenken Sie jedoch, dass copy nicht zwangsläufig eine tiefe Kopie erzeugt. Es kopiert lediglich die Elemente einer Liste indem deren Adressen kopiert werden. Ist Ihre Liste eine mehrdimensionale Liste, laufen Sie in das gleiche Problem:

row = [0, 1, 0, 1, 0, 1, 1]
picture = [row.copy(), row.copy()]
picture_copy = picture.copy()
picture_copy[0][0] = 1

print(picture[0][0])
print(picture_copy[0][0])

1
1

Tiefe Kopie in Python

Verwenden Sie die Funktion deepcopy des Moduls copy um eine tiefe Kopie in Python zu erzeugen.

Um Listen zu verketten, können Sie in Python den +-Operator verwenden.

[1,2,3,4] + [5,6,7,8]

[1, 2, 3, 4, 5, 6, 7, 8]

Das Ergebnis ist eine neue eindimensionale Liste die alle Elemente der beiden Listen in genau jener Reihenfolge enthält. Allerdings unterscheidet Python zwischen

mylist += other_list

und

mylist = mylist + other_list

Ersteres, also +=, führt eine veränderbare (engl. mutable) Konkatenation durch, d.h. hier wird mylist verändert. Letzteres, also mylist + other_list, führt eine unveränderbare (engl. immutable) Konkatenation durch, wodurch eine Kopie erzeugt wird. D.h. mylist = mylist + other_list erzeugt eine völlig neue Liste und ordnet es mylist zu.

Sie mögen nun denken, dass Ergebnis ist doch identisch? Sehen wir uns folgenden Code an:

def concat_immutable(list1,list2):
    concat = list1 + list2
    return concat

def concat_mutable(list1,list2):
    list1 += list2
    return list1

a = [1,2,3,4]
b = [5,6,7,8]
c = concat_immutable(a,b)
print(f'a = {a}')
print(f'b = {b}')
print(f'c = {c}')

c = concat_mutable(a,b)
print(f'a = {a}')
print(f'b = {b}')
print(f'c = {c}')

a = [1, 2, 3, 4]
b = [5, 6, 7, 8]
c = [1, 2, 3, 4, 5, 6, 7, 8]
a = [1, 2, 3, 4, 5, 6, 7, 8]
b = [5, 6, 7, 8]
c = [1, 2, 3, 4, 5, 6, 7, 8]

concat_mutable verändert list1 und da es sich nicht um einen primitiven Datentyp handelt, wird nur die Referenz kopiert und nicht die Liste a selbst. Somit wird a += b ausgeführt und a wird verändert. Dies bezeichnen wir als sogenannten Seiteneffekt und in diesem Fall ist es ein unerwarteter Seiteneffekt, den wir vermeiden sollten! Dennoch ist += immer dann sehr sinnvoll wenn Sie eine Liste sukzessive füllen wollen. Denn jedes Mal die gesamte Liste zu kopieren kann zu einer langen Laufzeit führen.

Exercise 22.3 (Immutable vs. Mutable)

Welcher der beiden Funktionen wird bei gleicher Eingabe in kürzerer Zeit ablaufen und warum? Testen Sie beide Versionen für große n > 0.

def my_range_mutable(n):
    number = []
    for i in range(n):
        number += [i]
    return number

def my_range_immutable(n):
    number = []
    for i in range(n):
        number = number + [i]
    return number

Um über die Elemente einer Liste zu iterieren, verwendet man in Python die for-Schleife und wie immer bestimmt die Einrückung die Strukturierung (Python verzichtet auf Klammern):

for row in picture:
    print(row)

[1, 1, 0, 1, 0, 1, 1]
[0, 1, 0, 1, 0, 1, 1]

Exercise 22.4 (Iteration)

Schreiben Sie einen Code der jedes Pixel des Bildes einzeln durch print() ausgibt.

Hide code cell source 
for row in picture:
    for pixel in row:
        print(pixel)

1
1
0
1
0
1
1
0
1
0
1
0
1
1

22.1.2. Funktionen in Python#

Funktionen definieren wir mit dem Schlüsselwort def gefolgt vom Funktionsnamen und den Parametern der Funktion sowie ihrer Logik. Die Werte, die diese Parameter beim Funktionsaufruf annehmen, nennen wir Argumente.

Falls Sie mit Ihrer Funktion einen Wert, eine Liste, oder ein anderes Objekt zurückgeben möchten nutzen Sie das return-Schlüsselwort. Zum Beispiel:

x = 10
c = 100
def add(x, y):
    c = x + y
    return c
add(15, x)

25

Die Variablen x und c außerhalb der Funktion befinden sich in einem anderen Namensraum. Deshalb bleiben diese unverändert.

Durch den obigen Aufruf wird der Parameter x auf eine Speicheradresse gesetzt, die auf den Wert 15 referenziert. y hingegen wird auf die Speicheradresse von x (welches sich außerhalb der Funktion befindet) gesetzt. c wird zu 25 und wird zurückgegeben.

Falls y innerhalb der Funktion verändert wird, würde Python eine neue Kopie des Werts im Speicher anlegen, da es sich um einen unveränderlichen (immutable) Datentyp handelt. Alle atomaren Datentypen wie int, float, bool aber auch str(Zeichenketten) und tuple sind unveränderlich. Listen jedoch nicht!

Eine gute Übung ist es eine mehrdimensionale Liste zu abzuflachen (engl. flatten), d.h., aus einer mehrdimensionalen Liste wird eine Liste, welche eine Dimension weniger hat erzeugt. Hierbei bleibt die Reihenfolge der Elemente gewöhnlich erhalten.

Exercise 22.5 (Flatten)

Schreiben Sie eine Funktion flatten(mylist), die die \(n\)-dimensionalen Liste mylist in eine \(n-1\)-dimensionale Liste transformiert. Zum Beispiel soll aus [[[1,2], [3,3]], [[1,3], [4,5]]], also einer \(3\)-dimensionalen Liste, [[1,2], [3,3], [1,3], [4,5]], also eine \(2\)-dimensionale Liste werden.

Hide code cell source 
def flatten(mylist):
    result = []
    for sub_list in mylist:
        for element in sub_list:
            result.append(element)

    return result

flatten([[[1,2], [3,3]], [[1,3], [4,5]]])

[[1, 2], [3, 3], [1, 3], [4, 5]]

In unserer Lösung bewirkt result.append(element) das gleich wie result += [element] jedoch ist die erste Version klarer zu lesen denn wir wollen das Element element anhängen (engl. append).

22.2. Informationserzeugung#

Exercise 22.6 (Bild generieren)

Generieren Sie ein weißes \(10 \times 10\) Rasterbild. Dieses soll einen schwarzen Rand besitzen, welches einen Pixel breit ist. Nutzen Sie die Programmierung um sich Zeit zu sparen!

Hide code cell source 
top = [0 for i in range(10)]
center = [0] + [1 for i in range(8)] + [0]
picture = [top.copy()] + [center.copy() for i in range(8)] + [top.copy()]
picture

[[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]

Auch bei der Erzeugung dieses Bilds müssen Sie darauf achten die richtige Art von Kopien zu erzeugen. Um sich Code zu sparen kann das sog. List-Comprehension Ihnen Zeit beim Schreiben sparen.

Exercise 22.7 (Bild manipulieren)

Testen Sie Ihr generiertes Bild. Ändern Sie den Pixel in der 5-ten Zeile und und 5-ten Spalte, sowie einen Pixeln in der ersten Spalte und einen in der ersten Zeile

Hide code cell source 
picture[4][4] = 1
picture

[[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
Hide code cell source 
picture[4][0] = 1
picture

[[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [1, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
Hide code cell source 
picture[0][4] = 1
picture

[[0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [1, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 1, 1, 1, 1, 1, 1, 1, 1, 0],
 [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]

Exercise 22.8 (Variables Bild generieren)

Schreiben Sie eine Funktion, die Ihnen ein weißes Bild mit schwarzem Rand generiert. Dabei soll die Breite width und Höhe height sowie die Randbreite border_width ein Parameter der Funktion sein.

Hide code cell source 
def generate_border_picture(width=10, height=10, border_width=1):
    picture = []
    
    yborder = min(border_width,height)
    xborder = min(border_width,width)
    top = [0 for _ in range(width)]
    for _ in range(yborder):
        picture.append(top.copy())
        
    for _ in range(height-2*border_width):
        picture.append(
            [0 for _ in range(xborder)] + 
            [1 for _ in range(width-2*border_width)] + 
            [0 for _ in range(xborder)])
    
    for _ in range(min(border_width,height-yborder)):
        picture.append(top.copy())
    return picture
generate_border_picture(width=5, height=10, border_width=2)

[[0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 1, 0, 0],
 [0, 0, 1, 0, 0],
 [0, 0, 1, 0, 0],
 [0, 0, 1, 0, 0],
 [0, 0, 1, 0, 0],
 [0, 0, 1, 0, 0],
 [0, 0, 0, 0, 0],
 [0, 0, 0, 0, 0]]

Exercise 22.9 (Variable Bildgenerierung testen)

Testen Sie Ihre Funktion insbesondere für besondere Werte wie border_width > width.

Exercise 22.10 (Variable Bildgenerierung testen)

Wie bereits erwähnt plottet folgende Funktion Ihr Bild.

import matplotlib.pyplot as plt
def plot_picture(picture):
    plt.imshow(picture, cmap='gray', vmin=0, vmax=1)

Sehen Sie sich die dazugehörige Dokumentation an und nutzen Sie die Funktion.

Mit folgendem Code können wir uns unser Bild anzeigen.

picture = generate_border_picture(width=5, height=10, border_width=1)
plot_picture(picture)
../../_images/abab4a4d5e9f1b922158c73e605766bc7d96cc9a99b7149bb856574f22b00adb.png

22.3. Informationsmanipulation#

Wir haben bereits jetzt ein neues Bildformat geschaffen und ein kleines Programm, welches unser Format interpretieren und als Rasterbild anzeigt. In anderen Worten, unsere erdachte Interpretation wurde realisiert.

Jetzt können wir uns austoben und weitere Bilder generieren. Wie wäre es zum Beispiel mit einem Kreis, Rechteck oder Dreieck? Diese Objekte direkt als Ansammlung von Pixeln zu beschreiben ist schwierig und unflexibel.

Was uns das Leben deutlich leichter macht, ist die Einführung einer weiteren Interpretation. Diese soll uns in eine abstraktere Welt ka­ta­pul­tie­ren. In anderen Worten: Wir konstruieren eine Interpretation die geometrische (mathematische) Objekten wie den Kreis, ein Rechteck oder Dreieck (Repräsentanten) in eine zweidimensionale Liste aus 0 und 1 (Bedeutung) übersetzt. Diese Übersetzung bezeichnet man auch als Rasterisierung (siehe Abschnitt Vektorgrafiken).

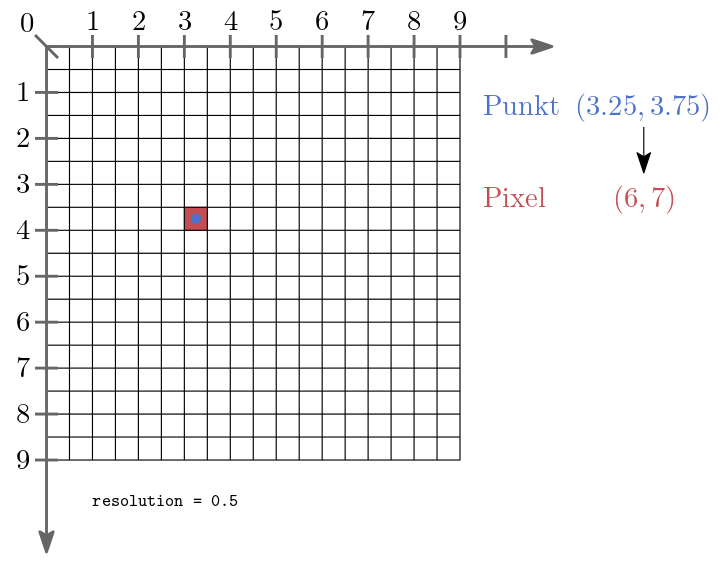
../../_images/point-to-pixel.png

Unsere geometrischen Objekte haben reelle Koordinaten z.B. können wir einen Kreis durch seinen Mittelpunkt \(c = (x,y)\) und Radius \(r\) eindeutig beschreiben. Um die Koordinaten in Pixelkoordinaten zu transformieren legen wir auf das Rasterbild ein reelles Koordinatensystem. Hat unser Bild \(n \times n\) Pixelbild und wir möchten den Raum \(10 \times 10 \subset \mathbb{R}^2\) durch das Bild abbilden, entspricht die erste Bildzeile dem Raum \(10 \times 1\).

Um keine Verzerrung zu erhalten sollten Pixel in \(x\) und in \(y\) Richtung gleich viel Anteil des Euklidischen Raumes überziehen. Die Auflösung resolution gibt an wie viel Raum ein Pixel repräsentiert. Bei einer resolution = 0.1 repräsentiert ein Pixel den Raum \(0.1 \times 0.1\). Anders ausgedrückt, braucht es \(10 \times 10\) Pixel um den Raum \(1 \times 1\) im \(\mathbb{R}^2\) zu repräsentieren.

Kennen wir die resolution, die Anzahl der Pixel in \(x\)-Richtung cols, die Anzahl der Pixel in \(y\)-Richtung rows und gehen davon aus, dass der Raum \(R\) den wir Abbilden möchten in \((0,0)\) beginnt und nur positive Werte enthält, also \(R = [0;w] \times [0;h]\), dann können wir für einen gegebenen Punkt \(p = (x,y) \in \mathbb{R}^2\) den Pixel \((i,j) \in \mathbb{N}^2\) berechnen der \(p\) enthält.

Exercise 22.11 (Pixel berechnen)

Schreiben Sie eine Funktion to_pixel(p, resolution) die Ihnen den Pixel (i,j) zurückgibt der den Punkt p = (x,y) enthält. Bedenken Sie, dass die Indexierung der Pixel mit 0 beginnt.

Hide code cell source 
def to_pixel(p, resolution):
    x, y = p
    return int(x / resolution), int(y/ resolution)

to_pixel((0.7, 0), 0.5)

(1, 0)

Soweit so gut! Widmen wir uns nun dem Problem ein Rechteck bzw. Dreieck zu zeichnen. Wir wenden die Mustererkennung an und bemerken, dass sowohl das Dreieck als auch das Rechteck aus Segmenten besteht (drei für das Dreieck und 4 für das Rechteck). Deshalb können wir das Problem in das Zeichnen mehrere Segmente zerteilen.

Ein Segment können wir durch zwei Punkte \(p_1 = (x_1, y_1)\) und \(p_2 = (x_2, y_2)\) definieren. Wir könnten aus den Punkten die Geradengleichung \(f(x) = mx + t\) berechnen und diese ‚abfahren‘. Hier würden wir jedoch auf unangenehme Sonderfälle stoßen. Zum Beispiel, lässt sich ein Segment was parallel zur \(y\)-Achse verläuft nicht durch eine Funktion beschreiben.

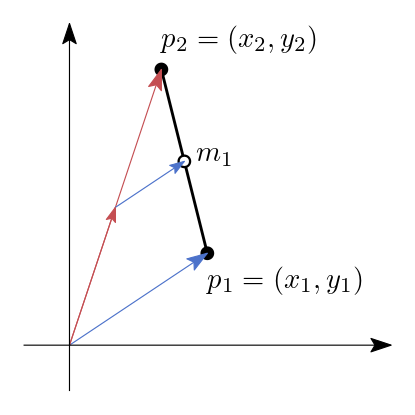
../../_images/midpoint.png

Was sagt uns folgende Beobachtung: Ist \(p_1, p_2\) gegeben dann ist der Mittelpunkt \(m_1 = ((x_1 + x_2)/2, (y_1 + y_2)/2)\) Teil des Segments. Außerdem erhalten wir neue Segmente \((p_1,m_1)\) und \((m_1,p_2)\). Wir können dies mit den beiden neuen Segmenten wiederholen und erhalten vier neue Segmente. Diesen Vorgang können wir solange fortsetzen, bis ein Segment komplett in einem Pixel enthalten ist und eine weitere Verfeinerung keine Wirkung mehr erzeugt.

Wir können diesen Vorgang rekursiv realisieren. Das heißt die Funktion, welche den Mittelpunkt berechnet, wird innerhalb dieser Funktion erneut aufgerufen. Das kann endlos so weiter gehen und wir müssen uns eine Abbruchbedingung überlegen.

Exercise 22.12 (Mittelpunkt berechnen)

Schreiben Sie eine Funktion midpoint(p1, p2) die Ihnen den Mittelpunkt (mx,my) des Segments (p1=(x1,y1), p2=(x2, y2)) zurückgibt.

Hide code cell source 
def midpoint(p1, p2):
    return (p1[0]+p2[0])/2, (p1[1]+p2[1])/2

midpoint((0,0),(3,3))

(1.5, 1.5)

Exercise 22.13 (Länge berechnen)

Schreiben Sie eine Funktion distance(p1,p2), die Ihnen die Länge des Segments (p1=(x1,y1), p2=(x2, y2)) zurückgibt.

Tipp: Sie können die Funktion sqrt der numpy Bibliothek verwenden, d.h.

import numpy as np
...
np.sqrt(...)
...

distance() können wir als Abbruchbedingung der Rekursion verwenden. Ist distance(p1,p2) <= resolution macht es keinen großen Sinn mehr das Segment (p1,p2) weiter zu verkleinern.

Exercise 22.14 (Segmentpunkte erzeugen)

Schreiben Sie eine Funktion line(p1, p2, resolution), die Ihnen Punkte des Segments (p1,p2) erzeugt und als Liste zurückgibt.

Hide code cell source 
import numpy as np
def distance(p1, p2):
    return np.sqrt((p1[0]-p2[0])**2 + (p1[1]-p2[1])**2)

def split(p1, p2, resolution, points):
    if distance(p1,p2) <= resolution:
        return points
    m1 = midpoint(p1, p2)
    points.append(m1)
    split(p1,m1,resolution,points)
    split(m1,p2,resolution,points)
    return points

def line(p1, p2, resolution):
    points = []
    split(p1, p2, resolution, points)
    return points
line((0,0),(3,0),0.1)

[(1.5, 0.0),
 (0.75, 0.0),
 (0.375, 0.0),
 (0.1875, 0.0),
 (0.09375, 0.0),
 (0.28125, 0.0),
 (0.5625, 0.0),
 (0.46875, 0.0),
 (0.65625, 0.0),
 (1.125, 0.0),
 (0.9375, 0.0),
 (0.84375, 0.0),
 (1.03125, 0.0),
 (1.3125, 0.0),
 (1.21875, 0.0),
 (1.40625, 0.0),
 (2.25, 0.0),
 (1.875, 0.0),
 (1.6875, 0.0),
 (1.59375, 0.0),
 (1.78125, 0.0),
 (2.0625, 0.0),
 (1.96875, 0.0),
 (2.15625, 0.0),
 (2.625, 0.0),
 (2.4375, 0.0),
 (2.34375, 0.0),
 (2.53125, 0.0),
 (2.8125, 0.0),
 (2.71875, 0.0),
 (2.90625, 0.0)]

Mit line können wir Punkte eines Segments erzeugen und durch to_pixel können wir diese Punkte in Pixel umwandeln. Lassen Sie uns ein Bild einer Geraden zeichnen:

resolution = 0.1
picture = generate_border_picture(width=100, height=100, border_width=0)
points = line((1,1), (9,9), resolution)
pixels = list(map(lambda point: to_pixel(point, resolution), points))
for pixel in pixels:
    picture[pixel[1]][pixel[0]] = 0
    
plot_picture(picture)
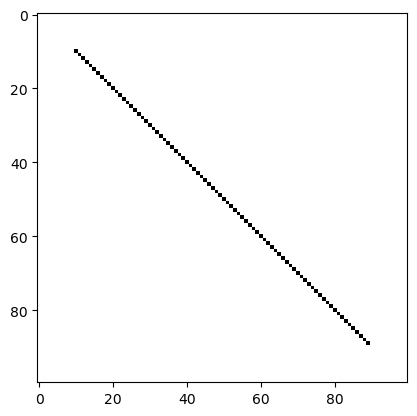
../../_images/34b6e315282f23a01bb0d6285818530a81ec8b60b79f3cf72bd9cd13ac4b070a.png

Das sieht schon recht gut aus. Da der Pixel picture[0][0] rechts oben ist, ist unser Koordinatensystem an der \(x\)-Achse gespiegelt und nach oben verschoben, was wir vernachlässigen können.

Exercise 22.15 (Linie zeichnen)

Schreiben Sie eine Funktion draw_line(picture, p1, p2, resolution), die das Segment (p1,p2) in das Bild picture hinein zeichnen. Behandeln Sie auch den Fall, dass das Segment nicht in das Bild passt (es soll dann kein Fehler erscheinen, sondern der Teil der nicht hinein passt wird abgeschnitten).

Hide code cell source 
def contains_pixel(picture, pixel):
    return pixel[0] >= 0 and pixel[0] < len(picture) and pixel[1] >= 0 and pixel[1] < len(picture[0])

def draw_line(picture, p1, p2, resolution):
    points= line(p1, p2, resolution)
    pixels = list(map(lambda point: to_pixel(point, resolution), points))
    for pixel in pixels:
        if contains_pixel(picture, pixel):
            picture[pixel[1]][pixel[0]] = 0

resolution = 0.1
picture = generate_border_picture(width=100, height=100, border_width=0)
draw_line(picture, (-1,-1), (11,11), resolution)
plot_picture(picture)
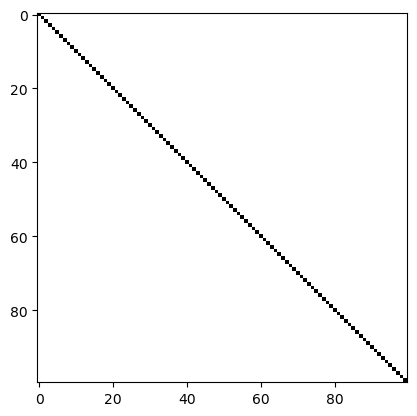
../../_images/7dd7ff07cd27a4c4f7f836992ea04e73a49d0332d787018bc53e18c538170a35.png

Jetzt haben wir alle Teilprobleme gelöst und können das Dreieck bzw. Rechteck zeichnen.

Exercise 22.16 (Dreieck zeichnen)

Schreiben Sie eine Funktion draw_triangle(picture, p1, p2, p3, resolution) die das Dreieck (p1,p2,p3) in das Bild picture hinein zeichnet.

Hide code cell source 
def draw_triangle(picture, p1, p2, p3, resolution):
    draw_line(picture, p1, p2, resolution)
    draw_line(picture, p2, p3, resolution)
    draw_line(picture, p3, p1, resolution)
    
resolution = 0.1
picture = generate_border_picture(width=100, height=100, border_width=0)
draw_triangle(picture, (1,1), (5,9), (9,1), resolution)
plot_picture(picture)
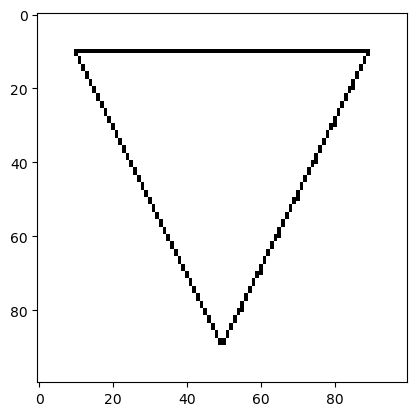
../../_images/2ba29e2aba72473666aaf051459099e46825bf6d6e9fabb33d30f868c8cca4d7.png

Exercise 22.17 (Rechteck zeichnen)

Schreiben Sie eine Funktion draw_rectangle(picture, p1, p2, p3, p4, resolution) die das Rechteck (p1,p2,p3,p4) in das Bild picture hinein zeichnet.

Hide code cell source 
def draw_rectangle(picture, p1, p2, p3, p4, resolution):
    draw_line(picture, p1, p2, resolution)
    draw_line(picture, p2, p3, resolution)
    draw_line(picture, p3, p4, resolution)
    draw_line(picture, p4, p1, resolution)
    
resolution = 0.1
picture = generate_border_picture(width=100, height=100, border_width=0)
draw_rectangle(picture, (1,1), (1,9), (9,9), (9,1), resolution)
plot_picture(picture)
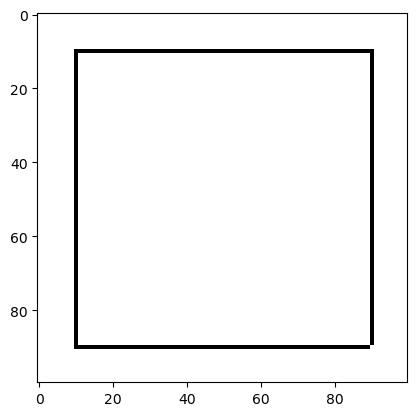
../../_images/595344a7f5235f8e5a42a607bd0d6c07da48b9ee7da3d2831a2e647cf1e7d5b2.png

Wenn wir uns die beiden Funktionen draw_triangle und draw_rectangle genauer ansehen und unsere Mustererkennung aktivieren, könnte uns etwas auffallen? Die Funktionen gleichen sich! Beide zeichnen eine Sequenz/Liste von zusammenhängenden Segmenten oder anders gesagt: Beide zeichnen ein Polygon!

Exercise 22.18 (Polygon zeichnen)

Schreiben Sie eine Funktion draw_polygon(picture, polygon, resolution) die das Polygon polygon = (p1,p2,p3,p4,p5,...) in das Bild picture hinein zeichnet. polygon kann eine Liste oder Tupel aus Punkten sein.

Annahme: Gehen Sie davon aus, dass die Reihenfolge der Punkte korrekt ist.

Hide code cell source 
def draw_polygon(picture, polygon, resolution):
    for i in range(len(polygon)):
        draw_line(picture, polygon[i-1], polygon[i], resolution)
    
resolution = 0.1
picture = generate_border_picture(width=100, height=100, border_width=0)
draw_polygon(picture, ((1,1), (1,9), (9,9), (9,1)), resolution)
plot_picture(picture)
../../_images/595344a7f5235f8e5a42a607bd0d6c07da48b9ee7da3d2831a2e647cf1e7d5b2.png

Dreieck, Rechteck und Polygon hätten wir geschafft. Für den Kreis \(K\) müssen wir zurück in unsere abstrakte Welt der geometrischen Objekte, denn einen Kreis mit lauter Segmenten darzustellen, ist möglich aber umständlich. Wir müsten erst ein Poylgon mit sehr vielen Segmenten berechnen.

Die Punkte eines Kreises lassen sich durch eine Kurve beschreiben. Sei der Kreis durch seinen Mittelpunkt \(m = (x_m, y_m)\) und den radius \(r\) beschrieben dann sind

\[K = \{(x_m + \cos(t) \cdot r, y_m + \sin(t) \cdot r) : t \in [0;2\pi]\}\]

die Punkte des Kreises bzw. der Kreis selbst. Um den Kreis zu zeichnen unterteilen wir einfach das Intervall \([0;2\pi]\) in \(n\) Teile und erhalten so \(n\) Punkte. Wir könnten z.B. \(n\) so wählen dass \(2\pi / n <\) resolution ist.

Exercise 22.19 (Kreis zeichnen)

Schreiben Sie eine Funktion draw_circle(picture, circle, resolution), die den Kreis circle = (m=(x,y), r) in das Bild picture hinein zeichnet. Sie können erneut numpy verwenden, d.h. np.sin(), np.cos(), np.pi und (optional) np.linspace().

Hide code cell source 
import numpy as np
def draw_circle(picture, circle, resolution):
    center = circle[0]
    radius = circle[1]
    n = int(6 * np.pi / resolution)
    t = np.linspace(start=0.0, stop=2 * np.pi, num=n)
    for dt in t:
        x = center[0] + np.cos(dt) * radius
        y = center[1] + np.sin(dt) * radius
        pixel = to_pixel((x, y), resolution)
        if contains_pixel(picture, pixel):
            picture[pixel[1]][pixel[0]] = 0
    
resolution = 0.1
picture = generate_border_picture(width=100, height=100, border_width=0)
draw_circle(picture, ((5,5), 3), resolution)
plot_picture(picture)
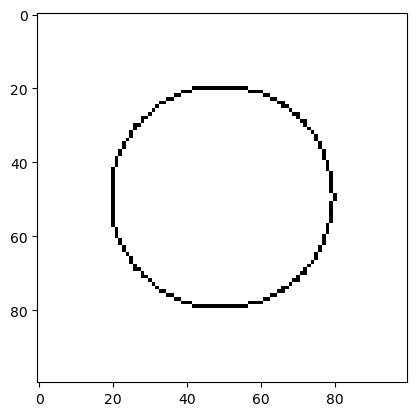
../../_images/47bf60be3dbe1dc6fa0f368f2f88eadac8683d67a4c26238a2f33254700ad6ba.png

Im Falle des Kreises beschreibt

\[k(t) = (x_m + \cos(t) \cdot r, y_m + \sin(t) \cdot r)\]

die Kurve des Kreises. Wir können aber auch andere Kurven wie zum Beispiel die Funktion \(f(x) = x^2\) durch die Kurve \(k(t) = (t, f(t))\) zeichnen. Durch wie viele Punkte die Funktion noch gut erkennbar ist, ist jedoch im allgemeinen nicht so einfach zu schätzen.

Exercise 22.20 ((mathematische) Funktion zeichnen)

Suchen Sie sich irgendeine geeignete Funktion aus und zeichnen Sie diese in einem geeigneten Intervall.

Hide code cell source 
import numpy as np
def draw_function(picture, f, start, stop, resolution):
    n = int(3 * (stop - start) / resolution)
    t = np.linspace(start=start, stop=stop, num=n)
    for dt in t:
        pixel = to_pixel((dt, f(dt)), resolution)
        if contains_pixel(picture, pixel):
            picture[pixel[1]][pixel[0]] = 0
            
resolution = 0.1
picture = generate_border_picture(width=100, height=100, border_width=0)
draw_function(picture, lambda t: (t-5)**2, 1, 9, resolution)
plot_picture(picture)
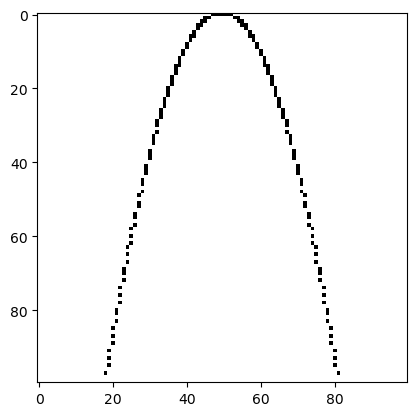
../../_images/9d17a0a374dc33371af59d3f3519ecd845bd8cdc8470eb083c9ff914793a5f68.png

22.4. Daumenkino#

Die folgende Methode (ein Interpreter) erwartet eine Liste von Bilder (in Ihrem Format) und generiert daraus eine Animation (eine Folge von Plots). Falls Sie den Parameter save auf True setzen, wird ein GIF (eine Bildfolge/Daumenkino/Minivideo) erzeugt und in der Datei 'binary-drawing.gif' abgespeichert.

import matplotlib.pyplot as plt
import matplotlib.animation as animation
from matplotlib import animation, rc
from IPython.display import HTML, display
from IPython.display import HTML

def animate(pictures, interval = 100, save = False, title = '', dpi = 80):
    cmap='gray'
    vmin = 0
    vmax = 1
    fig, ax = plt.subplots()
    plt.title(title)
    im = plt.imshow(pictures[0], animated=True, cmap = cmap, vmin = vmin, vmax = vmax)
    i = {'index': 0} # trick to enforce sideeffect
    def updatefig(*args):
        i['index'] += 1
        if i['index'] == len(pictures):
            i['index'] = 0
        im.set_array(pictures[i['index']])
        return im, 
    ani = animation.FuncAnimation(fig, updatefig, interval=interval, blit=True, save_count=len(pictures))
    if save:
        ani.save('binary-drawing.gif', dpi=dpi, writer="imagemagick")
    plt.close()
    return ani

Exercise 22.21 (Einfaches Daumenkino)

Generieren Sie folgendes GIF/Daumenkino bzw. Animation:

../../_images/daumenkino.gif

Tipp: Sie benötigen lediglich mehrere Aufrufe von generate_border_picture().

Hide code cell source 
size = 20
increase = [generate_border_picture(width=size, height=size, border_width=i) for i in range(size//2)]
decrease = [generate_border_picture(width=size, height=size, border_width=(size//2)-i) for i in range((size//2)-1)]
border_pictures = increase + decrease
ani = animate(border_pictures, save=True)
HTML(ani.to_jshtml())

MovieWriter imagemagick unavailable; using Pillow instead.

Fassen wir noch einmal kurz zusammen was wir bis jetzt geschafft haben: Wir haben uns ein Format / eine Interpretation für ein Schwarz-Weiß-Bild ausgedacht und umgesetzt. Mit ein wenig Hilfe durch externer Module, konnten wir unser Rasterbild anzeigen. Wir haben Algorithmen implementiert die uns Polygone (inkl. Dreiecke und Rechtecke), Kreise und sogar Funktionen zeichnen. Und jetzt haben wir sogar die Möglichkeit aus einer Folge von Bildern ein kleines Video zu generieren. Dieses Video ist wiederum nichts anderes als eine Liste von Listen von Listen bestehend aus Nullen und Einsen. Ist das nicht ganz erstaunlich?

Wir haben jetzt die Möglichkeit eine unbegrenzte Menge an Animationen zu erzeugen, von bewegten geometrischen Objekten bis hin zum Game Of Life - Ihre Kreativität ist das Limit.

Exercise 22.22 (Simulation eines Partikels)

Generieren Sie eine Animation eines Balls, welcher sich in einer Box bewegt, d.h. der Ball bewegt sich mit konstanter Geschwindigkeit und prallt von der Wand ab.

../../_images/daumenkino_ball.gif

Tipps: Schreiben Sie erst eine Methode die einen Kreis circle = (m = (x,y), r) in einer Box fortbewegt und diese Bewegung als Liste von Kreisen zurückgibt. Anschließend können Sie mit draw_circle() diese Liste in eine Liste von Bildern umwandeln. Bedenken Sie, dass sie für jeden Kreis ein neues Bild durch generate_border_picture() generieren müssen.

Hide code cell source 
def generate_ball_box(width, height, circle, resolution):
    w = int(width/resolution)
    h = int(height/resolution)
    picture = generate_border_picture(width=w, height=h, border_width=1)
    ball = draw_circle(picture, circle, resolution)
    return picture

def animate_ball(nframes):
    resolution = 0.1
    box_width = 10
    box_height = 10
    x = 5
    y = 5
    radius = 1
    velocity = [0.1,0.3]
    
    animation = []
    time = 1
    for i in range(nframes):
        # collision detection
        if x - radius <= 0 or x + radius >= box_width:
            velocity[0] = -velocity[0]
        if y - radius <= 0 or y + radius >= box_height:
            velocity[1] = -velocity[1]
        
        x = x + velocity[0] * time
        y = y + velocity[1] * time
        circle = ((x,y),radius)
        animation.append(generate_ball_box(box_width,box_height,circle,resolution))
    return animation

ani = animate(animate_ball(nframes=100), save=True)
HTML(ani.to_jshtml())

MovieWriter imagemagick unavailable; using Pillow instead.

Exercise 22.23 (Eigenes Daumenkino)

Erzeugen Sie Ihr eigenes Daumenkino. Vielleicht ein bewegtes Dreieck oder eine fortlaufende Sinuswelle oder etwas ganz anderes?

22.5. Fourier-Zeichnungen (optional)#

Was nun folgt ist ein sich Austoben in der Welt die wir uns geschaffen haben. Wir möchten Ihnen eine ganz bestimmte Zeichenmethode nicht vorenthalten.

Stellen Sie sich ein Blatt Papier vor. Auf diesem zeichnen Sie einen Kreis \(K_0\). Anhand dieses Kreises zeichnen Sie einen weiteren Kreis \(K_1\), sodass der Mittelpunkt von \(K_1\), während Sie zeichnen, auf \(K_0\) wandert. Nachdem Sie fertig sind, löschen Sie \(K_0\).

Ihr Ergebnis hängt davon ab, wie schnell sie auf \(K_0\) wandern und wie schnell Sie \(K_1\) zeichnen, d.h. das Ergebnis hängt von den Frequenzen und Radii ab.

Zeichnen Sie beide Kreise mit der gleichen Frequenz und starten Sie beide Kreise bei \(y = 0\), so ist \(K_1\) ein Kreis wobei dessen Radius die Summe der Radii der beiden Kreise ist.

Angenommen

\[K_0(t) = (x_0 + \cos(\omega_0 \cdot t) \cdot r_0, y_0 + \sin(\omega_0 \cdot t) \cdot r_0)\]

und

\[K_1(t) = (\cos(\omega_1 \cdot t) \cdot r_1, \sin(\omega_1 \cdot t) \cdot r_1)\]

dann gilt für ihre gezeichnete Kurve

\[K(t) = K_0(t) + K_1(t)\]

Wir können das weiter verallgemeinern und von \(n\) Kreisen ausgehen, dann gilt für ihre Zeichnung:

\[K(t) = \sum_{i=0}^{n-1} K_i(t)\]

Exercise 22.24 (Fourier-Zeichnungen)

Schreiben Sie eine Funktion draw_circular(picture, center, frequencies, radii, resolution, start stop), die die oben beschriebene Zeichentechnik implementiert. Dabei soll center gleich \((x_0, y_0)\), frequencies eine Liste die alle Frequenzen \(\omega_0, \ldots \omega_{n-1}\) und radii eine Liste die alle Radii \(r_0, \ldots, r_{n-1}\) enthält sein. start und stop sollen ihr (Zeichen-)Intervall definieren.

Als Motivation hier ein Beispiel:

resolution = 0.1
picture = generate_border_picture(width=100, height=100, border_width=0)
draw_circular(picture, (5,5), [4,15], [3,0.7], resolution, 0.0, 2*np.pi)
plot_picture(picture)

ergibt

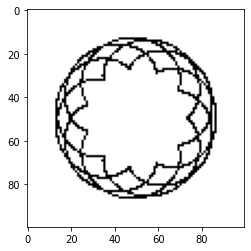
../../_images/fourier-drawing.png
Hide code cell source 
def draw_circular(picture, center, frequencies, radii, resolution, start=0.0, stop=2*np.pi):
    n = int(2*max(frequencies)*(stop-start) / resolution)
    t = np.linspace(start=start, stop=stop, num=n)
    for dt in t:
        x = center[0]
        y = center[1]
        
        for i in range(min(len(frequencies), len(radii))):
            radius = radii[i]
            frequency = frequencies[i]
            x = x + np.cos(frequency*dt) * radius
            y = y + np.sin(frequency*dt) * radius
        
        pixel = to_pixel((x, y), resolution)
        if contains_pixel(picture, pixel):
            picture[pixel[1]][pixel[0]] = 0
            
resolution = 0.1
picture = generate_border_picture(width=100, height=100, border_width=0)
draw_circular(picture, (5,5), [1,5,4], [2,1,0.5], resolution, 0.0, 2*np.pi)
plot_picture(picture)
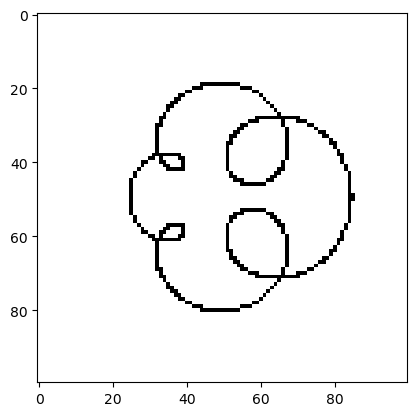
../../_images/2c403fa1bfcf9249dc9a802e67d190a34f8ef6d20ef07f564e15c38178fa17d3.png

Es ergeben sich interessante Fragen. Zum Beispiel, mit welchen Argumenten erhalten Sie ein harmonisches (ein eher einfaches) Bild und warum? Wann erhalten Sie hingegen ein komplexeres Gebilde? Was hat das mit den harmonischen bzw. unharmonischen Schwingungen und einem harmonischen bzw. unharmonischen Ton zu tun? Können wir durch unsere Zeichenmethode Ton zeichnen? Welche Objekte können wir überhaupt mit dieser Methode zeichen, eine Gerade, ein Rechteck?

Falls Sie sich mehr mathematisches Wissen zu diesem Thema aneignen möchten, ist folgendes exzellentes Video von Grant Sanderson ein wunderbarer Einstieg.