Kontrollstrukturen

Inhalt

10.3. Kontrollstrukturen#

Durch Wiederholung in Form von Schleifen und (rekursiven) Funktionen vermeiden wir es Anweisungen, die wir mehrfach ausführen wollen, auch mehrfach niederzuschreiben. Erst durch diese fundamentale Eigenschaft, ist es überhaupt möglich, dass wir die Anzahl der ausgeführten Anweisungen von der Länge des Programmcodes entkoppeln.

Fallunterscheidungen erlauben es uns wiederum bestimmte Anweisungen nur dann auszuführen, wenn eine bestimmte Bedingung zur Laufzeit des Programms erfüllt ist.

Schleifen und Fallunterscheidungen kombiniert mit Variablen, bilden bereits alles was wir benötigen. Um unseren Programmcode zu strukturieren und bestimmte Programmteile an verschiedenen Stellen aufzurufen, gibt es zusätzlich das Konzept der Programmierfunktionen oder kurz Funktionen.

Kontrollstrukturen

Kontrollstrukturen sind Anweisungen, welche die Abarbeitungsreihenfolge von anderen Anweisungen, und damit den Programmablauf kontrollieren.

Zusammenfassend konzentrieren wir uns auf:

Fallunterscheidungen (bedingte Ausführung)
Schleifen (Wiederholung)
Funktionen (Wiederholung)

Wie bereits erwähnt, muss eine Programmiersprache nur sehr wenige und auch nur sehr primitive Kontrollstrukturen anbieten damit diese als Turing-vollständig gilt. Theoretisch ist es bereits ausreichend wenn eine Programmiersprache

Variablen unterstützt, auf die wir einen konstanten Wert addieren oder subtrahieren können und
eine Wiederholung unterstützt, dessen Abbruchbedingung vor dem Eintritt in die Wiederholung unbekannt ist (while-Schleife)

Die Fallunterscheidung, lässt sich (in hässlicher Form) durch eine Schleife ausdrücken.

10.3.1. Fallunterscheidungen#

Die erste Kontrollstruktur realisiert die bedingte Ausführung, das bedeutet, eine bestimmte Sequenz von Anweisungen A1, ... ,An wird nur dann ausgeführt, wenn eine Bedingung B zutrifft.

if B:
    A1
    ...
    An

Die Bedingung B kann nur zu wahr True oder falsch False ausgewertet werden. Gewöhnlich hängt der Wahrheitswert der Bedingung vom Programmablauf ab, d.h., er ist erst zur Laufzeit bekannt. Zum Beispiel gibt folgendes Programm 'you win!' mit einer (pseudo) Wahrscheinlichkeit von 50% aus, da der Variablen x ein Zufallswert zwischen 0 und 1 (Gleichverteilung) zugewiesen wird.

import random as rnd

x = rnd.random()
if x > 0.5:
    print('you win!')

you win!

Es gibt von diesen Fallunterscheidungen verschiedene Varianten, wobei diese lediglich syntaktischer Zucker sind. Für Python besprechen wir alle Möglichkeiten im Teil PYTHON in Kontrollstrukturen.

10.3.2. Wiederholung#

Das fundamentale Prinzip der Wiederholung ist zentraler Bestandteil des Computational Thinkings. Blicken wir in den Werkzeugkasten der Algorithmen so finden wir die Wiederholung überall. Sortieralgorithmen, die Berechnung eines Gleichungssystems, das Verarbeiten eines Bildes, die Schaltflächen einer App, überall finden wir Schleifen, die unsere Informationen iterativ verarbeiten.

Nach der Definition eines Algorithmus, muss dieser aus endlich vielen Anweisungen bestehen. Will man jedoch eine variable Menge an Information verarbeiten, so muss ein Algorithmus, abhängig von der Eingabegröße, unterschiedlich viele Anweisungen ausführen. Das bedeutet, dass die Länge des Algorithmus (Textlänge) unabhängig von der Anzahl der auszuführenden Anweisungen (für eine gegebenen Eingabe) sein muss! Nach dem Schubfachprinzip bedeutet dies wiederum, dass in diesem Fall Teile des Algorithmus öfters durchlaufen werden - Wiederholung muss also in irgendeiner Form stattfinden.

Überraschenderweise hat sich herausgestellt, dass Wiederholung in Kombination mit der Fallunterscheidung ausreicht, um alles berechnen zu können was wir bisher als natürlich berechenbar ansehen. Nach der unbeweisbaren Church-Turing-These werden wir kein Problem finden, welches natürlich berechenbar aber nicht durch einen Computer berechnet werden kann. Die Fallunterscheidung in Kombination mit der Wiederholung ist scheinbar ausreichend.

Nun haben Sie vielleicht die Hoffnung, Sie müssten nur die Wiederholung und die Fallunterscheidungen beherrschen und können dann jedes Problem lösen. Leider sind diese beiden Techniken derart grundlegend, dass sie eine notwendige nicht aber ausreichende Bedingung für die Entwicklung von Algorithmen darstellen. Wir können das mit der Sprache vergleichen. Nur weil wir Laute von uns geben können, heißt das nicht, dass wir uns in jeder Sprache verständigen können. Ein weiteres Beispiel wären die Naturwissenschaften. Nur weil wir die kleinsten Teilchen im Universum verstehen, bedeutet dass nicht, dass wir damit das entstehen von Leben oder andere komplexe Übergängen erklären können.

Wir kennen zwei Arten von Wiederholungen:

Die Iteration und
die Rekursion.

Auf der konzeptionellen Ebene erscheinen Iteration und Rekursion grundverschieden – es sind unterschiedliche Denkweisen. Wir können rekursiv oder iterativ denken.

Iteration und Rekursion

Jede Rekursion kann in eine unbestimmte Iteration und jede (unbestimmte) Iteration in eine Rekursion umgewandelt werden.

Mit unbestimmt meinen wir, dass bevor die Iteration beginnt nicht bekannt ist, wie viele Wiederholungen nötig sind.

Manche Probleme lassen sich leichter rekursiv und andere leichter iterativ lösen bzw. durchdenken. In manchen Fällen ist es beispielsweise sinnvoll eine rekursive Lösung zu entwickeln und diese dann in eine iterative umzuwandeln.

10.3.2.1. Iteration#

Wenn Sie Erfahrung im entwickeln von iterativen Algorithmen gesammelt haben und iterative Algorithmen analysiert und verwendet haben, dann werden Sie beginnen in Iterationen zu denken. Sie werden beginnen in Iterationen von Iterationen von Iterationen zu denken.

Das wohl einfachste Beispiel für eine Iteration ist die Addition einer Menge von Zahlen. Lassen Sie uns alle geraden Zahlen von 2 bis n addieren. Hierzu brauchen wir eine Variable acc, welche wir mit dem Wert 0 initialisieren und dann iterativ 2 dann 4, und so weiter addieren.

acc = 0
n = 100
for k in range(2,n,2):
    acc += k

acc

acc = 0
n = 100
k = 2
while k < n:
    acc += k
    k += 2

acc

Betrachten wir einen etwas komplizierteren Algorithmus: Den Bubblesort Algorithmus. Dieser sortiert eine Liste von vergleichbaren Objekten. Wir gehen durch die Liste (1. Iterationen) und wann immer zwei nebeneinander liegende Zahlen falsch sortiert sind, vertauschen wir diese. Wir wiederholen dies (2. Iterationen) solange bis keine zwei benachbarte Zahlen falsch sortiert sind.

import random as rnd

def bubble_sort(numbers):
    finished = False
    while(not finished):
        finished = True
        for i in range(1,len(numbers)):
            if numbers[i] < numbers[i-1]:
                numbers[i], numbers[i-1] = numbers[i-1], numbers[i]
                finished = False
    
numbers = [1,2,3,4,5,6,7,8,9]
rnd.shuffle(numbers)
print(f'before sorting: {numbers}')
bubble_sort(numbers)
print(f'after sorting: {numbers}')

before sorting: [3, 4, 6, 9, 1, 8, 2, 5, 7]
after sorting: [1, 2, 3, 4, 5, 6, 7, 8, 9]

Die beiden Schleifen liefern uns auch einen Hinweis auf die Laufzeit dieses simplen Sortieralgorithmus. Nach jedem ausführen der inneren Schleife befindet sich ein neues Element an seiner korrekten Position. Damit brauchen wir maximal so viele Durchläufe (1. Iterationen) wie es Elemente sind. Jeder Durchlauf benötigt ebenfalls maximal so viel Schritte wie es Elemente sind. Damit hat der Algorithmus im schlechtesten Fall eine quadratische Laufzeit. Das bedeutet, wollen wir \(n\) Zahlen sortieren ist die Zeitkomplexität des Algorithmus gleich \(\mathcal{O}(n^2)\).

Exercise 10.2 (Fallunterscheidung durch Schleife)

Schreiben Sie ein Programm, welches den Algorithmus von oben (die zufällige Ausgabe von 'you win!') realisiert, ohne eine Fallunterscheidung zu verwenden.

Solution to Exercise 10.2 (Fallunterscheidung durch Schleife)

import random as rnd

x = rnd.random()
for i in range(int(0.5+x)):
    print('you win!')

10.3.2.2. Rekursion#

Rekursion ist dieses scheinbar unverständliche Konzept, welches Mathematiker*innen lieben und vor dem Programmierer*innen anfänglich davonlaufen. Derweil würden wir behaupten, dass die rekursive Denkweise uns Menschen näher ist als das Denken in Iterationen. Rekursive Lösungen sind oft eleganter, kürzer, verständlicher aber leider auch langsamer als iterative Lösungen. Die Rekursion hängt dabei stark mit der Induktion zusammen, siehe Abschnitt vollständige Induktion.

Nehmen wir die Berechnung der Fakultät, einmal iterativ

\[\text{fac}_\text{it}(n) = n \cdot (n-1) \cdot (n-2) \cdot \ldots \cdot 1 = \prod\limits_{i=1}^n i\]

def fac_it(n):
    result = 1
    for i in range(1,n+1):
        result *= i
    return result

fac_it(5)

und einmal rekursiv

\[\begin{split}\text{fac}_\text{rec}(n) = \begin{cases} 1 & \text{ falls } n = 0\\ n \cdot \text{fac}_\text{rec}(n-1) & \text{ sonst}\end{cases}\end{split}\]

def fac_rec(n):
    if n <= 1:
        return 1
    return n * fac_rec(n-1)

fac_rec(5)

Die Rekursion beinhaltet einen Selbstbezug, wohingegen die iterative Lösung diesen ausbreitet bzw. auflöst. Betrachten wir die rekursive Lösung benötigen wir für die Berechnung lediglich die Multiplikation und den Selbstbezug - keine Schleife, und abgesehen von n, nicht einmal eine Variable.

Rekursion

Als Rekursion wird ein Vorgang bezeichnet, welcher sich selbst als Teil enthält oder mithilfe von sich selbst definierbar ist.

10.3.2.3. Die Türme von Hanoi#

Probleme lassen sich immer dann leichter rekursiv lösen, wenn der Selbstbezug offensichtlich oder einfach zu finden ist. Ein Beispiel sind die sog. Türme von Hanoi.

Ein Turm bestehend aus \(n\) unterschiedlich breiten Schichten soll von einem Ort 0 zu einem anderen Ort 2 gebracht werden. Der Turm wird nach oben immer schmaler, d.h., die Schicht die über einer anderen liegt ist schmaler. Wir können nur eine einzelne Schicht bewegen und wir dürfen keine Schicht auf eine schmälere legen. Es gibt nur einen zusätzlichen Ablegeort 1. Wie bringen wir den Turm nun von Ort 0 nach Ort 2?

(1) Induktionsanfang: Hat der Turm nur eine Schicht, ist das Problem schnell gelöst: Bewege Schicht von 0 nach 2.

Besteht der Turm aus zwei Schichten, ist das Problem auch noch einfach zu lösen:

Bewege oberste Schickt von 0 nach 1.
Bewege unterste Schicht von 0 nach 2 und
Bewege dann die schmälere Schicht von 1 auf 2.

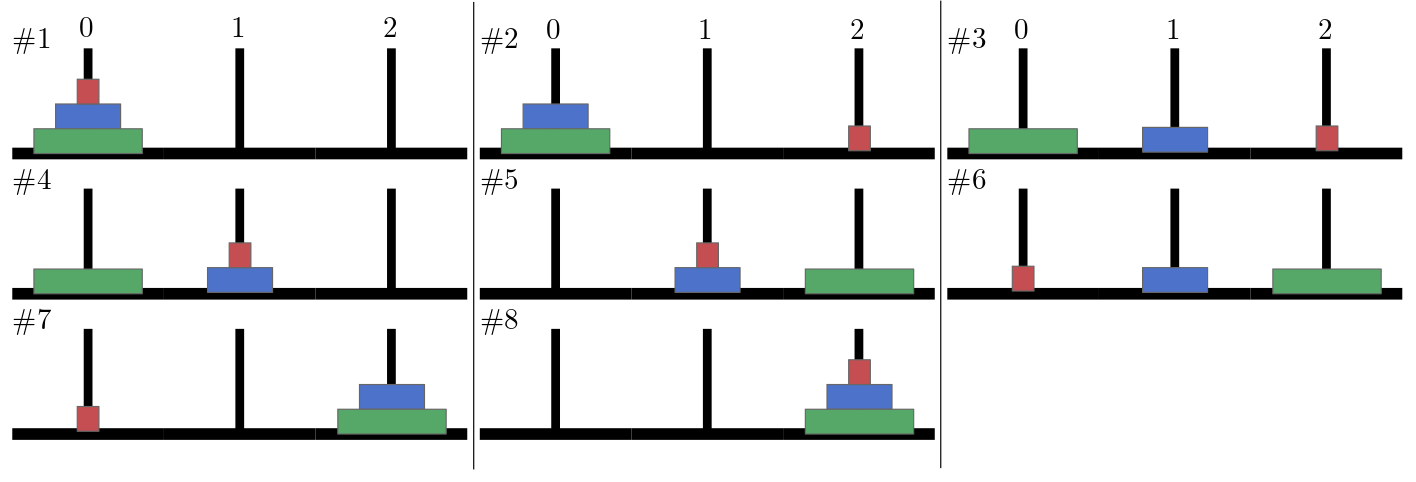
../../_images/hanoi.png — Abb. 10.2 Die Türme von Hanoi mit drei Schichten.#

Wie gehen wir aber für einen allgemeinen Fall mit \(n\) Schichten vor?

(2) Induktionsschritt: Nun,

wir bringen die obersten \(n-1\) Schichten von 0 nach 1,
die unterste Schicht von 0 nach 2 und dann
die \(n-1\) Schichten von 1 nach 2.

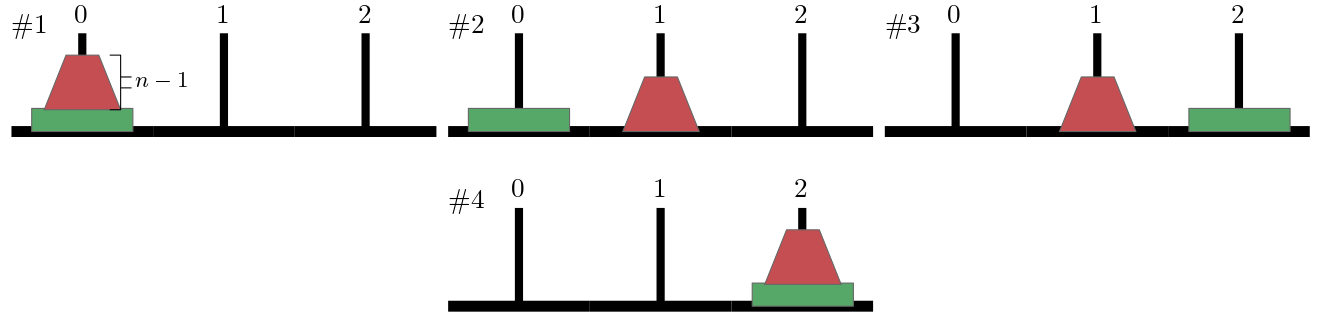
../../_images/hanoi-abstract.png — Abb. 10.3 Die Türme von Hanoi mit \(n\) Schichten.#

Diese \(n-1\) Schichten sind ein Turm, der um eine Schicht kleiner ist. Auch die eine Schicht ist ein Turm, bestehend aus nur einer Schicht. Aus dem Problem einen Turm der Höhe \(n\) zu verschieben wurde: Verschiebe Turm der Höhe \(n-1\) (Selbstbezug) + Verschiebe eine Scheibe (Rest).

Rekursiv zu denken bedeutet oft, dass wir einfach mal davon ausgehen, wir hätten das Problem bereits gelöst. Wir schreiben in einem deklarativen Stil, d.h., wir schreiben hin was wir wollen und nicht was wir tun. Wir gehen also davon aus es gäbe eine Funktion move_tower(n, fr, to, tmp), welche die obersten n Schichten eines Turms von fr nach to bringt und dabei tmp als Zwischenablage verwendet.

def move_tower(n, fr, to, tmp):
    pass

unter dieser Annahme bewegen wir den Turm wie oben beschrieben:

def move_tower(n, fr, to, tmp):
    if n == 1:
        move(fr, to)             # real move from upper most stone
    
    move_tower(n-1, fr, tmp, to) # eg 0 -> 1
    move_tower(1, fr, to, tmp)   # eg 0 -> 2
    move_tower(n-1, tmp, to, fr) # eg 1 -> 2

Um das ganze vorzuführen modellieren wir einen Turm als Liste von Zahlen und die drei Plätze als Liste der Länge 3.

def move(hanoi, fr, to):
    hanoi[to].insert(0, hanoi[fr][0])
    del hanoi[fr][0]

def move_tower(hanoi, n, fr, to, spare):
    if n == 1:
        move(hanoi, fr, to)
    else:    
        move_tower(hanoi, n-1, fr, spare, to)
        move_tower(hanoi, 1, fr, to, spare)
        move_tower(hanoi, n-1, spare, to, fr)

n = 6
tower = list(range(n))
hanoi = [tower, [], []]
print(hanoi)

move_tower(hanoi, n, 0, 2, 1)
print(hanoi)

[[0, 1, 2, 3, 4, 5], [], []]
[[], [], [0, 1, 2, 3, 4, 5]]

Erstaunlich, wie kurz die Lösung am Ende ausfällt. Es fühlt sich fast so an als hätten wir an irgendeiner Stelle betrogen.

Aber Vorsicht! Zu beweisen, dass der Algorithmus korrekt funktioniert ist nicht trivial. In anderen Worten, es ist nicht offensichtlich, dass der Algorithmus korrekt ist dennoch ist es intuitiv plausibel. Wir die Korrektheit mit einem Induktionsbeweis zeigen. Dazu müssen wir zeigen:

Induktionsschritt: Zeige \(A(n_0)\), d.h., move_tower liefert das korrekte Ergebnis für einen Turm der aus nur einer Scheibe besteht (\(n_0 = 1\))
Induktionsschritt: Zeige \(A(n) \Rightarrow A(n+1)\), d.h. falls move_tower das richtige Ergebnis für Turm mit \(n\) Schreiben liefert, dann liefert die Funktion auch das richtige Ergebnis für \(n+1\) Scheiben.

Um eine gute iterative Lösung zu finden braucht es Gehirnschmalz, doch denken Sie daran: Es gibt sie immer!

Exercise 10.3 (Türme von Hanoi)

Zeigen Sie, dass der oben beschriebene Algorithmus das korrekte Ergebnis liefer.