Namensregister

Inhalt

24. Namensregister#

Sie kennen womöglich gar keinen ausgedruckten Namensregister mehr. Vor langer langer Zeit in einer weit entfernten Galaxie gab es noch so etwas wie Telefonbücher und zwar als wirkliches reales Buch! In einem solchen Buch standen die Telefonnummern der Menschen, welche in einem bestimmten Ort wohnen.

Lernziel

In der Übung Speicher - alles ist eine Liste hatten wir uns angesehen, wie eine Liste im Arbeitsspeicher realisiert wird. In dieser Übung lernen Sie wie aus dieser Liste mittels einer Hashfunktion die zweite wichtige Datenstruktur, das Wörterbuch / Dictionary entsteht. Sie werden Ihr eigenes Wörterbuch Schritt für Schritt entwickeln.

Ein Telefonbuch liefert Ihnen für einen gegebenen Namen die zugehörige Telefonnummer der Familie oder Person. Falls es keine zwei Personen mit dem gleichen Haushalt gibt, so können wir das Telefonbuch als mathematische Funktion interpretieren. Der Definitionsbereich sind die Namen der Haushalte und der Wertebereich ist die Menge zugehörigen Telefonnummern.

Warum ist ein Buch voller Namen und Telefonnummern nützlich? Welche wesentliche Eigenschaft des Telefonbuchs macht es nützlich?

Exercise 24.1 (Eigenschaft des Telefonbuch)

Aufgrund welcher Eigenschaft finden wir im Telefonbuch eine Telefonnummer recht schnell?

Solution to Exercise 24.1 (Eigenschaft des Telefonbuch)

Das Telefonbuch ist eine nach Namen sortierte Liste von Einträgen!

24.1. Binäre Suche im Telefonbuch#

24.1.1. Informelle Beschreibung#

Wenn wir in einer solchen sortierten Liste nach einem Eintrag suchen gehen wir intuitiv anders vor als wenn die Liste unsortiert wäre. Im Fall der unsortierten Liste bleibt uns nichts anderes übrig als die Liste von vorne bis hinten zu durchsuchen (lineare Suche).

Exercise 24.2 (Suchen im Telefonbuch)

Beschreiben Sie informell, wie Sie nach der Telefonnummer von Fr. Reichel suchen.

Solution to Exercise 24.2 (Suchen im Telefonbuch)

Wir schätzen erst ab wo die Namen mit dem Buchstaben R beginnen. Wir schlagen das Buch recht weit hinten auf und betrachten den ersten und letzten Namen der Seite. Ist der erste Name lexikographisch kleiner und der letzte lexikographisch größer als Reichel, so suchen wir den Namen auf der Seite.

Ist der erste Name lexikographisch größer als Reichel, finden wir den Namen im vorderen Teil des Buches. Ist der letzte Name lexikographisch kleiner als Reichel, finden wir den Namen im hinteren Teil des Buches.

Wir nehmen den entsprechenden Teil und schlagen die Seite in der Mitte dieses Teils auf. Den anderen Teil werden wir nie wieder betrachten.

Diesen Prozess wiederholen wir bis wir die entsprechende Seite gefunden haben. Dann können wir entweder den Namen auf der Seite mit einer linearen Suche auffinden oder die gleiche binäre Suche mit den Namen auf der Seite vollziehen.

Im Abschnitt Sprechen in der Taucherglocke haben wir unter Suchalgorithmen bereits diese sogenannte binäre Suche angewendet. Wir möchten an dieser Stelle ein wenig Formalismus einbringen um eine eindeutigere Beschreibung der binäre Suche zu erhalten. Wie jede neue Sprache kann der Formalismus abschreckend wirken, doch bietet er ähnlich wie die Programmiersprachen eine Möglichkeit sich unmissverständlich auszudrücken.

24.1.2. Formale Beschreibung#

Bei dieser Gelegenheit stellen wir Ihnen ein häufig verwendetes Konstrukt, den sog. Komperator, vor. Sei also \(E\) eine Menge von möglichen Einträgen. Sei \(\mathcal{L} = (e_0, \ldots, e_n), e_i \in E\) ein (geordnetes) Tupel. Sei

(24.1)#\[f_E : E \times E \rightarrow \{-1,0,1 \}\]

eine (Komparator-)Funktion (Comparator) oder kurz Komparator bezüglich \(E\). Dieser vergleicht zwei Elemente \(e_i, e_j \in E\) sodass

(24.2)#\[\begin{split}f_E(e_i, e_j) = \begin{cases} -1, & \quad \text{falls } e_i < e_j\\ +1, & \quad \text{falls } e_i > e_j\\ +0, & \quad \text{sonst}. \end{cases}\end{split}\]

Aus \(f_E\) lassen sich die Vergleichsoperatoren rekonstruieren:

(24.3)#\[\begin{gather} e_i < e_j \iff f(e_i, e_j) = -1 \\ e_i = e_j \iff f(e_i, e_j) = +0 \\ e_i > e_j \iff f(e_i, e_j) = +1. \end{gather}\]

Für das Tupel nehmen wir an dass

(24.4)#\[i < j \Rightarrow f_E(e_i, e_j) \leq 0 ,\]

das heißt, das Tupel ist sortiert.

Wir suchen nun ein Element \(e \in E\). Schrittweise zerteilen wir die Liste oder das Tupel \(\mathcal{L}\) in zwei gleiche Hälften und wählen eine davon. Dabei passen wir das Intervall \(I = [a;b]\) der Listenindices an, welche diese Hälften definieren.

Wir beginnen mit \(a_0 = 0, b_0 = |\mathcal{L}|-1\) und berechnen ein Pivotindex

\[k_0 = a_0 + \left \lfloor{(b_0 - a_0) / 2}\right \rfloor\]

Dabei ist \(\left \lfloor{\cdot}\right \rfloor\) das Abrunden. Falls das Pivotelement \(e_{k_0}\) gleich dem gesuchten Element \(e\) ist also

\[f_E(e, e_{k_0}) = 0,\]

sind wir fertig. Ansonsten passen wir das Suchintervall \(I_0 = [a_0;b_0]\) wie folgt an:

\[\begin{split} a_1 = \begin{cases} k_0+1, & \quad \text{falls } f_E(e, e_{k_0}) = 1\\ a_0, & \quad \text{sonst} \end{cases} \end{split}\]

\[\begin{split} b_1 = \begin{cases} k_0-1, & \quad \text{falls } f_E(e, e_{k_0}) = -1\\ b_0, & \quad \text{sonst} \end{cases} \end{split}\]

Wir haben ein neues Intervall \(I_1 = [a_1;b_1]\) und wiederholen die Schritte für die Intervallanpassung bis für irgendeine Iteration \(j\)

\[e_{k_j} = e\]

oder

\[a_j < b_j\]

gilt.

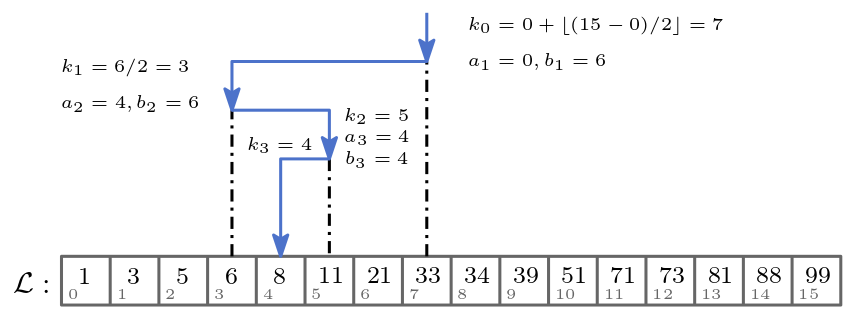
../../_images/binary-search.png — Abb. 24.1 Binäre Suche nach dem Element \(e = 8\) in einer sortierten Liste \(\mathcal{L}\) aus Zahlen.#

Zuweisung (Notation)

Falls wir uns der mathematischen Schreibweise bedienen vermeiden wir die Zuweisung über das \(=\) Zeichen. \(a = 2\) bedeutet, dass \(a\) gleich \(2\) ist. Der Ausdruck

\[a = a + 2\]

ist eine falsche Aussage. Oben haben wir stattdessen viele Variablen verwendet also

\[a_1 = a_0 + 2.\]

Stattdessen können wir auch einen anderen Operator verwenden. Üblich ist

\[a \leftarrow a + 2.\]

Lassen Sie uns ein Beispiel durchgehen. Angenommen wir haben eine Liste mit \(100\) Zahlen und wir suchen die Zahl \(e_i\) mit dem Index \(i = 66\). So ist folgende Sequenz die Sequenz der Intervalle:

\[[0;99], [50;99], [50;73], [62;73], [62;66], [65;66], [66;66]\]

Exercise 24.3 (Binäre Suchen - Intervalle)

Bestimmen Sie die Sequenz der Intervalle für eine Liste mit \(150\) Elementen und \(i = 48\).

Solution to Exercise 24.3 (Binäre Suchen - Intervalle)

\[[0;149], [0;73], [37;73], [37;54], [46;54], [46;49], [48;49]\]

24.1.3. Algorithmische Beschreibung#

Die wesentliche Eigenschaft welche die binäre Suche ausnutzt sind in Gleichungen (24.1), (24.2) und (24.4) zusammengefasst. Wir benötigen eine Ordnung, sodass es einen Komparator \(f_E\) gibt. Das Tupel bzw. unsere Liste muss sortiert sein (24.4).

Der Komparator \(f_E\) wird passend zur Menge der möglichen Listenelemente \(E\) definiert, d.h. je nachdem welche Art von Liste (Namensliste, Telefonbucheinträge, Zahlen, Klausuren) wir vorfinden, müssen wir ein geeignetes \(f_E\) konstruieren.

Zum Beispiel ist für die Klausuren \(f_E(e_i, e_j)\) gleich \(-1\) wenn der Name des Studierenden der Klausur \(e_i\) lexikographisch kleiner ist als der Name des Studierenden der Klausur \(e_j\). \(f_E\) abstrahiert alle unwichtigen Eigenschaften der Elemente der gegebenen Liste \(\mathcal{L}\).

Wie das passende \(f_E\) definiert ist, wissen wir als Entwickler*innen des Suchalgorithmus nicht und müssen es auch nicht wissen. Durch \(f_E\) haben wir das Problem in zwei Teilprobleme zerlegt:

Die Definition des Komparators \(f_E\), der zur Sortierung der Elemente passt und
die Suche unter der Annahme eines wohldefinierten Komparators.

Wir lösen lediglich das zweite Teilproblem. Um ersteres müssen sich die Anwender*innen unseres Suchalgorithmus kümmern. Durch diese Abstraktion schaffen wir es einen Suchalgorithmus zu entwickeln, der jede beliebige sortierte Liste durchsuchen kann!

Wir haben aber noch ein Problem! Nach was wollen wir denn eigentlich Suchen. In der formalen Beschreibung vergleichen wir die Elemente in der Liste mit dem gesuchten Element. Doch dieses gesuchte Element wollen wir ja gerade finden! Wir kennen es nicht aber wir kennen etwas mit dem wir es identifizieren können. Im Fall des Telefonbuchs, kennen wir den Nachnamen des Eintrags (Elements). Der Nachname ist ein sogenannter Schlüssel, der ein Element eindeutig identifiziert.

Erneut können wir diesen Schlüssel herausabstrahieren. Erneut erfolgt dies durch eine Funktion

\[g: E \rightarrow \mathcal{K},\]

wobei \(\mathcal{K}\) die Menge der Schlüssel ist. Da wir demnach Schlüssel vergleichen ändern wir den Komperator \(f_E\) zu

\[f_\mathcal{K}: \mathcal{K} \times \mathcal{K} \rightarrow \{-1,0,1 \}\]

Exercise 24.4 (Binäre Suche mit Komperator)

Transformieren Sie die formale Beschreibung (erneut) in eine Python Funktion binary_search(key, mylist, f, g), welche Ihnen das Element mit dem Schlüssel key zurückgibt.

Hinweis: In Python ist es möglich Funktionen einer anderen Funktion als Argument zu übergeben.

Ganzahlendivision (Python)

Teilen wir in Python zwei ganze Zahlen mit / so erhalten wir eine Fließkommazahl selbst wenn die Division eine Ganzzahl ergeben würde!

print(3/2)
print(type(3/2))
print(4/2)
print(type(4/2))

Python bietet aber auch die Ganzzahlendivision // an bei der das Ergebnis immer eine Ganzzahl ist. Es wird dabei stets auf die nächst liegende ganze Zahl abgerundet.

print(3//2)
print(type(3//2))
print(4//2)
print(type(4//2))

def binary_search(key, mylist, f, g = lambda x : x):
    a = 0
    b = len(mylist)-1
    k = (b-a) // 2
    while b-a >= 0:
        if f(key, g(mylist[k])) == 0:
            return mylist[k]
        elif f(key, g(mylist[k])) == -1:
            b = k-1
        else:
            a = k+1
        k = a + (b-a) // 2
    return None

In unserer Lösung belegen wir g mit der Identität als Standardargument. Das heißt, wenn die Anwender*innen kein g spezifizieren, gehen wir davon aus, dass

\[\mathcal{K} = E\]

gilt.

Exercise 24.5 (Binäre Suche von Zahlen mit Komperator)

Definieren Sie einen passenden Komparator cmp_numbers(number1, number2) für eine Liste von ganzen Zahlen, d.h. \(E = \mathbb{Z}\) und testen Sie diesen und binary_search.

def cmp_numbers(number1, number2):
    if number1 < number2:
        return -1
    elif number1 > number2:
        return 1
    return 0

print(binary_search(1, [1,2,3,4,5], cmp_numbers))
print(binary_search(7, [1,2,3,4,5], cmp_numbers))
print(binary_search(-7, [1,2,3,4,5], cmp_numbers))

1
None
None

Lassen Sie uns noch das Telefonbuchbeispiel testen. Folgender Code generiert Ihnen durch den Aufruf der Funktion random_phone_book(n) ein zufälliges Telefonbuch mit 100 Einträgen (unser Telefonbuch hat keine Seiten sondern nur Einträge).

import names
import functools as func
import numpy as np

def random_phone_number():
    pre = "0"+func.reduce(lambda a, b : str(a) + str(b), np.random.randint(10, size=3), "")
    post = func.reduce(lambda a, b : str(a) + str(b), np.random.randint(10, size=7), "")
    return pre + "-" + post

def random_phone_book(n):
    telbook = [
        {'name': names.get_last_name(), 'phone_number': random_phone_number()} for _ in range(n)
    ]
    telbook = sorted(telbook, key=lambda x: x['name'])
    return telbook

telbook = random_phone_book(100)

Sie müssen den Code nicht verstehen. Für die Generierung eines zufälligen Namens bedienen wir uns eines Paketes names. Und auch für die zufällige Telefonnummer setzten wir auf das numpy Paket. Jeder Eintrag ist ein Dictionary der Form

{'name': name, 'phone_number': telnr}

Exercise 24.6 (Binäre Suche)

Generieren Sie sich ein zufälliges Telefonbuch und benutzten Sie die Funktion binary_search(key, mylist, f, g) um einen existierenden Namen key im Telefonbuch zu finden. Sie müssen ein geeignetes f und g definieren.

Tipp: Finden Sie heraus wie Python Zeichenketten vergleicht.

index = 66
key = telbook[index]['name']
g = lambda entry : entry['name']

def cmp_strings(name1, name2):
    if name1 < name2:
        return -1
    elif name1 > name2:
        return 1
    return 0
    

print(binary_search(key, telbook, cmp_strings, g))

{'name': 'Obrien', 'phone_number': '0403-2362942'}

Zeichenkettenvergleich (Python)

In Python werden Zeichenketten lexikographisch verglichen. Zum Beispiel ergibt

"Abraham" < "Anna"

True. Jedoch müssen sie auf die Klein- und Großschreibung achten. So ergibt

"abraham" < "Anna"

False. Kleinbuchstaben sind also lexikographisch größer als Großbuchstaben.

24.2. Fächer und Markierungen#

An Telefonbüchern finden sich häufig Markierungen, welche die Suche weiter beschleunigen. Für jeden Buchstaben finden wir oft eine Markierung, sodass wir genau wissen wo wir Namen mit dem Anfangsbuchstaben, z.B. C, finden. Anstatt die binäre Suche über alle Einträge durchzuführen, müssen wir lediglich alle Einträge, die mit C starten betrachten.

Exercise 24.7 (Unterstützte binäre Suche)

Angenommen jeder Buchstabe kommt als Anfangsbuchstabe gleich häufig vor. Wie viele Schritte (Intervallanpassungen) sparen Sie sich durch die Markierungen, wenn ihr Telefonbuch 20 000 Einträge enthält?

Solution to Exercise 24.7 (Unterstützte binäre Suche)

Wir starten mit \(20 000 / 26 \approx 769\).

\[20 000 \cdot 2^{-5} < 769 < 20 000 \cdot 2^{-4}\]

Damit sparen wir uns \(5\) Schritte.

Eine weitere Variante Dinge zu Ordnen ist diese in unterschiedliche leicht identifizierbare Fächer zu packen. Wir könnten zum Beispiel für jeden Anfangsbuchstaben ein Fach eröffnen und alle Seiten des Telefonbuchs in das jeweilige Fach packen. Dafür müssten wir das Buch natürlich zerschneiden.

Diese zwei Varianten möchten wir uns ansehen

Fächer: Eine zweidimensionale Liste.
Markierungen: Eine eindimensionale Liste unterstützt durch eine Liste aus Markierungen.

Dazu werden wir zunächst Namen aus einer Datei einlesen und doppelte Einträge löschen.

24.2.1. Eine CSV Datei lesen#

Lassen Sie uns diese Markierungen nutzten. Wir werden dafür eine Liste der beliebtesten 1000 Mädchen- und Jungen-Namen von 1880 bis 2009 in den USA verwenden. Die Datei ist eine CSV (Comma Seperated Value) Datei. Eine solche Datei hat meist einen sogenannten Header (Kopfzeile) gefolgt von den jeweiligen Daten. In unserem Fall sieht der Inhalt der Datei wie folgt aus.

"year","name","percent","sex"
1880,"John",0.081541,"boy"
1880,"William",0.080511,"boy"
1880,"James",0.050057,"boy"
1880,"Charles",0.045167,"boy"
1880,"George",0.043292,"boy"
...

Wir möchten aus dieser Datei lediglich die Namen also die Spalte name extrahieren. Mit dem bekannten Modul Pandas können wir mit solchen Dateien bzw. Daten sehr viel einfacher umgehen. Doch hier möchten wir selbst Hand anlegen.

Der folgende Code öffnet die Datei baby-names.csv und ließt diese, sodass nach der Ausführung names alle Namen von baby-names.csv enthält (auch doppelte Einträge). babynames ist eine Sequenz von gelesenen Zeilen der CSV. Durch next(babynames) überspringen wir die Kopfzeile. Die for-Schleife iteriert über alle Zeilen. Jede Zeile row beinhaltet für jede Spalte einen Eintrag. row[0] ist das Jahr year und row[0] der Name name, den wir extrahieren möchten.

from csv import reader

def read_babynames():
    names = []
    with open('baby-names.csv') as file:
        babynames = reader(file, delimiter=',')
        next(babynames)
        for row in babynames:
            names.append(row[1])
    return names

names = read_babynames()
names

Show code cell output Hide code cell output

['John',
 'William',
 'James',
 'Charles',
 'George',
 'Frank',
 'Joseph',
 'Thomas',
 'Henry',
 'Robert',
 'Edward',
 'Harry',
 'Walter',
 'Arthur',
 'Fred',
 'Albert',
 'Samuel',
 'David',
 'Louis',
 'Joe',
 'Charlie',
 'Clarence',
 'Richard',
 'Andrew',
 'Daniel',
 'Ernest',
 'Will',
 'Jesse',
 'Oscar',
 'Lewis',
 'Peter',
 'Benjamin',
 'Frederick',
 'Willie',
 'Alfred',
 'Sam',
 'Roy',
 'Herbert',
 'Jacob',
 'Tom',
 'Elmer',
 'Carl',
 'Lee',
 'Howard',
 'Martin',
 'Michael',
 'Bert',
 'Herman',
 'Jim',
 'Francis',
 'Harvey',
 'Earl',
 'Eugene',
 'Ralph',
 'Ed',
 'Claude',
 'Edwin',
 'Ben',
 'Charley',
 'Paul',
 'Edgar',
 'Isaac',
 'Otto',
 'Luther',
 'Lawrence',
 'Ira',
 'Patrick',
 'Guy',
 'Oliver',
 'Theodore',
 'Hugh',
 'Clyde',
 'Alexander',
 'August',
 'Floyd',
 'Homer',
 'Jack',
 'Leonard',
 'Horace',
 'Marion',
 'Philip',
 'Allen',
 'Archie',
 'Stephen',
 'Chester',
 'Willis',
 'Raymond',
 'Rufus',
 'Warren',
 'Jessie',
 'Milton',
 'Alex',
 'Leo',
 'Julius',
 'Ray',
 'Sidney',
 'Bernard',
 'Dan',
 'Jerry',
 'Calvin',
 'Perry',
 'Dave',
 'Anthony',
 'Eddie',
 'Amos',
 'Dennis',
 'Clifford',
 'Leroy',
 'Wesley',
 'Alonzo',
 'Garfield',
 'Franklin',
 'Emil',
 'Leon',
 'Nathan',
 'Harold',
 'Matthew',
 'Levi',
 'Moses',
 'Everett',
 'Lester',
 'Winfield',
 'Adam',
 'Lloyd',
 'Mack',
 'Fredrick',
 'Jay',
 'Jess',
 'Melvin',
 'Noah',
 'Aaron',
 'Alvin',
 'Norman',
 'Gilbert',
 'Elijah',
 'Victor',
 'Gus',
 'Nelson',
 'Jasper',
 'Silas',
 'Christopher',
 'Jake',
 'Mike',
 'Percy',
 'Adolph',
 'Maurice',
 'Cornelius',
 'Felix',
 'Reuben',
 'Wallace',
 'Claud',
 'Roscoe',
 'Sylvester',
 'Earnest',
 'Hiram',
 'Otis',
 'Simon',
 'Willard',
 'Irvin',
 'Mark',
 'Jose',
 'Wilbur',
 'Abraham',
 'Virgil',
 'Clinton',
 'Elbert',
 'Leslie',
 'Marshall',
 'Owen',
 'Wiley',
 'Anton',
 'Morris',
 'Manuel',
 'Phillip',
 'Augustus',
 'Emmett',
 'Eli',
 'Nicholas',
 'Wilson',
 'Alva',
 'Harley',
 'Newton',
 'Timothy',
 'Marvin',
 'Ross',
 'Curtis',
 'Edmund',
 'Jeff',
 'Elias',
 'Harrison',
 'Stanley',
 'Columbus',
 'Lon',
 'Ora',
 'Ollie',
 'Russell',
 'Pearl',
 'Solomon',
 'Arch',
 'Asa',
 'Clayton',
 'Enoch',
 'Irving',
 'Mathew',
 'Nathaniel',
 'Scott',
 'Hubert',
 'Lemuel',
 'Andy',
 'Ellis',
 'Emanuel',
 'Joshua',
 'Millard',
 'Vernon',
 'Wade',
 'Cyrus',
 'Miles',
 'Rudolph',
 'Sherman',
 'Austin',
 'Bill',
 'Chas',
 'Lonnie',
 'Monroe',
 'Byron',
 'Edd',
 'Emery',
 'Grant',
 'Jerome',
 'Max',
 'Mose',
 'Steve',
 'Gordon',
 'Abe',
 'Pete',
 'Chris',
 'Clark',
 'Gustave',
 'Orville',
 'Lorenzo',
 'Bruce',
 'Marcus',
 'Preston',
 'Bob',
 'Dock',
 'Donald',
 'Jackson',
 'Cecil',
 'Barney',
 'Delbert',
 'Edmond',
 'Anderson',
 'Christian',
 'Glenn',
 'Jefferson',
 'Luke',
 'Neal',
 'Burt',
 'Ike',
 'Myron',
 'Tony',
 'Conrad',
 'Joel',
 'Matt',
 'Riley',
 'Vincent',
 'Emory',
 'Isaiah',
 'Nick',
 'Ezra',
 'Green',
 'Juan',
 'Clifton',
 'Lucius',
 'Porter',
 'Arnold',
 'Bud',
 'Jeremiah',
 'Taylor',
 'Forrest',
 'Roland',
 'Spencer',
 'Burton',
 'Don',
 'Emmet',
 'Gustav',
 'Louie',
 'Morgan',
 'Ned',
 'Van',
 'Ambrose',
 'Chauncey',
 'Elisha',
 'Ferdinand',
 'General',
 'Julian',
 'Kenneth',
 'Mitchell',
 'Allie',
 'Josh',
 'Judson',
 'Lyman',
 'Napoleon',
 'Pedro',
 'Berry',
 'Dewitt',
 'Ervin',
 'Forest',
 'Lynn',
 'Pink',
 'Ruben',
 'Sanford',
 'Ward',
 'Douglas',
 'Ole',
 'Omer',
 'Ulysses',
 'Walker',
 'Wilbert',
 'Adelbert',
 'Benjiman',
 'Ivan',
 'Jonas',
 'Major',
 'Abner',
 'Archibald',
 'Caleb',
 'Clint',
 'Dudley',
 'Granville',
 'King',
 'Mary',
 'Merton',
 'Antonio',
 'Bennie',
 'Carroll',
 'Freeman',
 'Josiah',
 'Milo',
 'Royal',
 'Dick',
 'Earle',
 'Elza',
 'Emerson',
 'Fletcher',
 'Judge',
 'Laurence',
 'Neil',
 'Roger',
 'Seth',
 'Glen',
 'Hugo',
 'Jimmie',
 'Johnnie',
 'Washington',
 'Elwood',
 'Gust',
 'Harmon',
 'Jordan',
 'Simeon',
 'Wayne',
 'Wilber',
 'Clem',
 'Evan',
 'Frederic',
 'Irwin',
 'Junius',
 'Lafayette',
 'Loren',
 'Madison',
 'Mason',
 'Orval',
 'Abram',
 'Aubrey',
 'Elliott',
 'Hans',
 'Karl',
 'Minor',
 'Wash',
 'Wilfred',
 'Allan',
 'Alphonse',
 'Dallas',
 'Dee',
 'Isiah',
 'Jason',
 'Johnny',
 'Lawson',
 'Lew',
 'Micheal',
 'Orin',
 'Addison',
 'Cal',
 'Erastus',
 'Francisco',
 'Hardy',
 'Lucien',
 'Randolph',
 'Stewart',
 'Vern',
 'Wilmer',
 'Zack',
 'Adrian',
 'Alvah',
 'Bertram',
 'Clay',
 'Ephraim',
 'Fritz',
 'Giles',
 'Grover',
 'Harris',
 'Isom',
 'Jesus',
 'Johnie',
 'Jonathan',
 'Lucian',
 'Malcolm',
 'Merritt',
 'Otho',
 'Perley',
 'Rolla',
 'Sandy',
 'Tomas',
 'Wilford',
 'Adolphus',
 'Angus',
 'Arther',
 'Carlos',
 'Cary',
 'Cassius',
 'Davis',
 'Hamilton',
 'Harve',
 'Israel',
 'Leander',
 'Melville',
 'Merle',
 'Murray',
 'Pleasant',
 'Sterling',
 'Steven',
 'Axel',
 'Boyd',
 'Bryant',
 'Clement',
 'Erwin',
 'Ezekiel',
 'Foster',
 'Frances',
 'Geo',
 'Houston',
 'Issac',
 'Jules',
 'Larkin',
 'Mat',
 'Morton',
 'Orlando',
 'Pierce',
 'Prince',
 'Rollie',
 'Rollin',
 'Sim',
 'Stuart',
 'Wilburn',
 'Bennett',
 'Casper',
 'Christ',
 'Dell',
 'Egbert',
 'Elmo',
 'Fay',
 'Gabriel',
 'Hector',
 'Horatio',
 'Lige',
 'Saul',
 'Smith',
 'Squire',
 'Tobe',
 'Tommie',
 'Wyatt',
 'Alford',
 'Alma',
 'Alton',
 'Andres',
 'Burl',
 'Cicero',
 'Dean',
 'Dorsey',
 'Enos',
 'Howell',
 'Lou',
 'Loyd',
 'Mahlon',
 'Nat',
 'Omar',
 'Oran',
 'Parker',
 'Raleigh',
 'Reginald',
 'Rubin',
 'Seymour',
 'Wm',
 'Young',
 'Benjamine',
 'Carey',
 'Carlton',
 'Eldridge',
 'Elzie',
 'Garrett',
 'Isham',
 'Johnson',
 'Larry',
 'Logan',
 'Merrill',
 'Mont',
 'Oren',
 'Pierre',
 'Rex',
 'Rodney',
 'Ted',
 'Webster',
 'West',
 'Wheeler',
 'Willam',
 'Al',
 'Aloysius',
 'Alvie',
 'Anna',
 'Art',
 'Augustine',
 'Bailey',
 'Benjaman',
 'Beverly',
 'Bishop',
 'Clair',
 'Cloyd',
 'Coleman',
 'Dana',
 'Duncan',
 'Dwight',
 'Emile',
 'Evert',
 'Henderson',
 'Hunter',
 'Jean',
 'Lem',
 'Luis',
 'Mathias',
 'Maynard',
 'Miguel',
 'Mortimer',
 'Nels',
 'Norris',
 'Pat',
 'Phil',
 'Rush',
 'Santiago',
 'Sol',
 'Sydney',
 'Thaddeus',
 'Thornton',
 'Tim',
 'Travis',
 'Truman',
 'Watson',
 'Webb',
 'Wellington',
 'Winfred',
 'Wylie',
 'Alec',
 'Basil',
 'Baxter',
 'Bertrand',
 'Buford',
 'Burr',
 'Cleveland',
 'Colonel',
 'Dempsey',
 'Early',
 'Ellsworth',
 'Fate',
 'Finley',
 'Gabe',
 'Garland',
 'Gerald',
 'Herschel',
 'Hezekiah',
 'Justus',
 'Lindsey',
 'Marcellus',
 'Olaf',
 'Olin',
 'Pablo',
 'Rolland',
 'Turner',
 'Verne',
 'Volney',
 'Williams',
 'Almon',
 'Alois',
 'Alonza',
 'Anson',
 'Authur',
 'Benton',
 'Billie',
 'Cornelious',
 'Darius',
 'Denis',
 'Dillard',
 'Doctor',
 'Elvin',
 'Emma',
 'Eric',
 'Evans',
 'Gideon',
 'Haywood',
 'Hilliard',
 'Hosea',
 'Lincoln',
 'Lonzo',
 'Lucious',
 'Lum',
 'Malachi',
 'Newt',
 'Noel',
 'Orie',
 'Palmer',
 'Pinkney',
 'Shirley',
 'Sumner',
 'Terry',
 'Urban',
 'Uriah',
 'Valentine',
 'Waldo',
 'Warner',
 'Wong',
 'Zeb',
 'Abel',
 'Alden',
 'Archer',
 'Avery',
 'Carson',
 'Cullen',
 'Doc',
 'Eben',
 'Elige',
 'Elizabeth',
 'Elmore',
 'Ernst',
 'Finis',
 'Freddie',
 'Godfrey',
 'Guss',
 'Hamp',
 'Hermann',
 'Isadore',
 'Isreal',
 'Jones',
 'June',
 'Lacy',
 'Lafe',
 'Leland',
 'Llewellyn',
 'Ludwig',
 'Manford',
 'Maxwell',
 'Minnie',
 'Obie',
 'Octave',
 'Orrin',
 'Ossie',
 'Oswald',
 'Park',
 'Parley',
 'Ramon',
 'Rice',
 'Stonewall',
 'Theo',
 'Tillman',
 'Addie',
 'Aron',
 'Ashley',
 'Bernhard',
 'Bertie',
 'Berton',
 'Buster',
 'Butler',
 'Carleton',
 'Carrie',
 'Clara',
 'Clarance',
 'Clare',
 'Crawford',
 'Danial',
 'Dayton',
 'Dolphus',
 'Elder',
 'Ephriam',
 'Fayette',
 'Felipe',
 'Fernando',
 'Flem',
 'Florence',
 'Ford',
 'Harlan',
 'Hayes',
 'Henery',
 'Hoy',
 'Huston',
 'Ida',
 'Ivory',
 'Jonah',
 'Justin',
 'Lenard',
 'Leopold',
 'Lionel',
 'Manley',
 'Marquis',
 'Marshal',
 'Mart',
 'Odie',
 'Olen',
 'Oral',
 'Orley',
 'Otha',
 'Press',
 'Price',
 'Quincy',
 'Randall',
 'Rich',
 'Richmond',
 'Romeo',
 'Russel',
 'Rutherford',
 'Shade',
 'Shelby',
 'Solon',
 'Thurman',
 'Tilden',
 'Troy',
 'Woodson',
 'Worth',
 'Aden',
 'Alcide',
 'Alf',
 'Algie',
 'Arlie',
 'Bart',
 'Bedford',
 'Benito',
 'Billy',
 'Bird',
 'Birt',
 'Bruno',
 'Burley',
 'Chancy',
 'Claus',
 'Cliff',
 'Clovis',
 'Connie',
 'Creed',
 'Delos',
 'Duke',
 'Eber',
 'Eligah',
 'Elliot',
 'Elton',
 'Emmitt',
 'Gene',
 'Golden',
 'Hal',
 'Hardin',
 'Harman',
 'Hervey',
 'Hollis',
 'Ivey',
 'Jennie',
 'Len',
 'Lindsay',
 'Lonie',
 'Lyle',
 'Mac',
 'Mal',
 'Math',
 'Miller',
 'Orson',
 'Osborne',
 'Percival',
 'Pleas',
 'Ples',
 'Rafael',
 'Raoul',
 'Roderick',
 'Rose',
 'Shelton',
 'Sid',
 'Theron',
 'Tobias',
 'Toney',
 'Tyler',
 'Vance',
 'Vivian',
 'Walton',
 'Watt',
 'Weaver',
 'Wilton',
 'Adolf',
 'Albin',
 'Albion',
 'Allison',
 'Alpha',
 'Alpheus',
 'Anastacio',
 'Andre',
 'Annie',
 'Arlington',
 'Armand',
 'Asberry',
 'Asbury',
 'Asher',
 'Augustin',
 'Auther',
 'Author',
 'Ballard',
 'Blas',
 'Caesar',
 'Candido',
 'Cato',
 'Clarke',
 'Clemente',
 'Colin',
 'Commodore',
 'Cora',
 'Coy',
 'Cruz',
 'Curt',
 'Damon',
 'Davie',
 'Delmar',
 'Dexter',
 'Dora',
 'Doss',
 'Drew',
 'Edson',
 'Elam',
 'Elihu',
 'Eliza',
 'Elsie',
 'Erie',
 'Ernie',
 'Ethel',
 'Ferd',
 'Friend',
 'Garry',
 'Gary',
 'Grace',
 'Gustaf',
 'Hallie',
 'Hampton',
 'Harrie',
 'Hattie',
 'Hence',
 'Hillard',
 'Hollie',
 'Holmes',
 'Hope',
 'Hyman',
 'Ishmael',
 'Jarrett',
 'Jessee',
 'Joeseph',
 'Junious',
 'Kirk',
 'Levy',
 'Mervin',
 'Michel',
 'Milford',
 'Mitchel',
 'Nellie',
 'Noble',
 'Obed',
 'Oda',
 'Orren',
 'Ottis',
 'Rafe',
 'Redden',
 'Reese',
 'Rube',
 'Ruby',
 'Rupert',
 'Salomon',
 'Sammie',
 'Sanders',
 'Soloman',
 'Stacy',
 'Stanford',
 'Stanton',
 'Thad',
 'Titus',
 'Tracy',
 'Vernie',
 'Wendell',
 'Wilhelm',
 'Willian',
 'Yee',
 'Zeke',
 'Ab',
 'Abbott',
 'Agustus',
 'Albertus',
 'Almer',
 'Alphonso',
 'Alvia',
 'Artie',
 'Arvid',
 'Ashby',
 'Augusta',
 'Aurthur',
 'Babe',
 'Baldwin',
 'Barnett',
 'Bartholomew',
 'Barton',
 'Bernie',
 'Blaine',
 'Boston',
 'Brad',
 'Bradford',
 'Bradley',
 'Brooks',
 'Buck',
 'Budd',
 'Ceylon',
 'Chalmers',
 'Chesley',
 'Chin',
 'Cleo',
 'Crockett',
 'Cyril',
 'Daisy',
 'Denver',
 'Dow',
 'Duff',
 'Edie',
 'Edith',
 'Elick',
 'Elie',
 'Eliga',
 'Eliseo',
 'Elroy',
 'Ely',
 'Ennis',
 'Enrique',
 'Erasmus',
 'Esau',
 'Everette',
 'Firman',
 'Fleming',
 'Flora',
 'Gardner',
 'Gee',
 'Gorge',
 'Gottlieb',
 'Gregorio',
 'Gregory',
 'Gustavus',
 'Halsey',
 'Handy',
 'Hardie',
 'Harl',
 'Hayden',
 'Hays',
 'Hermon',
 'Hershel',
 'Holly',
 'Hosteen',
 'Hoyt',
 'Hudson',
 'Huey',
 'Humphrey',
 'Hunt',
 'Hyrum',
 'Irven',
 'Isam',
 'Ivy',
 'Jabez',
 'Jewel',
 'Jodie',
 'Judd',
 'Julious',
 'Justice',
 'Katherine',
 'Kelly',
 'Kit',
 'Knute',
 'Lavern',
 'Lawyer',
 'Layton',
 ...]

24.2.2. Zählen von doppelten Einträgen#

Exercise 24.8 (Zählen doppelter Einträge)

Schreiben Sie eine Funktion count(name, names), welche die Anzahl der Einträge in names, die gleich name sind, zurückgibt. Zählen Sie die Vorkommen von John.

def count(name, names):
    count = 0
    for entry in names:
        if entry == name:
            count +=1 
    return count

count("John", names)

Wir möchten nun die Anzahl aller Namen in names zählen. Diese Anzahl sagt uns wie oft ein Name von 1880 bis 2008 in den Top 1000 der beliebtesten Namen in den USA war. Dazu legen wir ein Dictionary an, wobei der Schlüssel key des Dictionarys ein Name ist und dessen Wert value angibt wie oft dieser Name vorkommt. Zum Beispiel:

countings = {'John': 234, 'Anna': 201, ...}

Wir haben die folgenden beiden Funktionen entwickelt:

def count_all(names):
    countings = {}
    for name in names:
        if name in countings:
            countings[name] = count(name, names)
    return countings

und

def count_all(names):
    countings = {}
    for name in names:
        if name in countings:
            countings[name] += 1
        else:
            countings[name] = 1
    return countings

Exercise 24.9 (Zählen aller Einträge)

Welche der beiden Varianten ist die bessere? Begründen Sie Ihre Antwort.

Solution to Exercise 24.9 (Zählen aller Einträge)

Die zweite Variante ist die bessere, da sie das gleiche Ergebnis in weniger Schritten erzeugt. count iteriert durch die gesamte Liste names deshalb benötigen wir in der ersten Variante \(n \cdot n\) Schritte und in der zweiten Variante nur \(n\) Schritte, wobei \(n\) die Länge der Liste names ist.

Dieses Beispiel zeigt, dass es nicht immer von Vorteil ist, ein größeres Problem (count_all) durch Teilprobleme (count) zu lösen.

Interessanterweise haben wir durch unser Zählen auch gleich alle doppelten Einträge gelöscht, denn wenn wir nun alle Schlüssel des Dictionary in eine Liste packen, so beinhaltet diese keine doppelten Einträge mehr.

Exercise 24.10 (Einzigartige Einträge)

Sammeln Sie nun alle Schlüssel ein und packen Sie diese in eine Liste.

countings = count_all(names)
unique_names = list(countings.keys())

In Karten sortieren haben wir selbst einen Sortieralgorithmus entworfen. Selbstverständlich hat Python bereits einen solchen Algorithmus im Angebot. Diesen haben wir oben beim Generieren des zufälligen Telefonbuchs verwendet.

sorted?

bzw.

help(sorted)

Help on built-in function sorted in module builtins:

sorted(iterable, /, *, key=None, reverse=False)
    Return a new list containing all items from the iterable in ascending order.
    
    A custom key function can be supplied to customize the sort order, and the
    reverse flag can be set to request the result in descending order.

liefert Ihnen Hinweise darüber was die Funktion macht und wie sie zu benutzten ist.

Exercise 24.11 (Einzigartige Einträge sortieren)

Verwenden Sie sorted um unique_names

lexikographisch und
nach der Anzahl der Einträge in names (meist vorkommende Name ganz vorne in der Liste)

zu sortieren

unique_names_lex = sorted(unique_names)
unique_names_count = sorted(unique_names, key = lambda entry : countings[entry], reverse=True)

24.2.3. Ordnung durch Fächer#

Mit unique_names_lex haben wir eine lexikographisch sortierte Liste an beliebten Babynamen in den USA. Wäre es nicht praktisch sich die Namen, welche mit einem bestimmten Buchstaben beginnen aus der Liste herauszuziehen? Dies vereinfacht die Suche nach einem bestimmten Namen. Lassen Sie uns überdenken wie und warum wir Menschen Dinge in Fächern (engl. Buckets) ordnen.

Wie ordnen wir Menschen ganz alltägliche Dinge? Zum Beispiel in der Küche oder im Schlafzimmer? Gläser befinden sich in einem bestimmten Schrank, Teller in einem anderen. Das Besteck stecken wir in eine Schublade und diese ist oft so aufgeteilt, dass Messer, Löffel und Gabeln sich in je einem separierten Teil befinden. Hosen trennen wir von anderen Klamotten. Die Unterwäsche befindet sich an einer ganz bestimmten Stelle im Kleiderschrank. In einem Ordner sammeln wir Steuerunterlagen in dem anderen Arbeitsverträge oder Zeugnisse.

Warum machen wir das? Nun damit wir bestimmte Dinge schneller finden. Anstatt den gesamten Schrank nach einer Hose zu durchsuchen, müssen wir nur einen kleinen Teil durchwühlen. Diese Ordnung dient natürlich auch der Übersicht. So sehen wir sehr schnell, wie viele Hosen wir überhaupt besitzen und ob es Zeit wird sich mal wieder eine neue zu besorgen.

Die wesentliche Eigenschaft, die wir diesen Beispielen entziehen können ist, dass wir Dinge Fächern zuordnen. Diese Fächer können wir eindeutig und schnell identifizieren bzw. auf diese schnell zugreifen. So wissen wir in welcher Schublade sich das Besteck befindet und in welchem Unterabteil der Schublade wir zur Gabel greifen. Fächer können sortiert sein, z.B. sind unsere Hemden möglicherweise in einer ganz bestimmten Reihenfolge aufgehängt. Sie können aber auch unsortiert sein, z.B. sind alle Gabeln durcheinander in einem Schubladenabteil. Befindet sich eine bestimmte Art von Dingen in einem Fach so können wir uns einen Überblick über diese eine Art verschaffen.

Es ist kein Zufall, dass wir Menschen Dinge durch Fächer ordnen. Wir passen uns auch im Alltag den algorithmischen Strukturen an, die uns durch die Natur gegeben sind. Besonders bei den simpleren Datenstrukturen wird klar, dass es nicht die Informatiker*innen waren, die diese Strukturen erfunden haben. Sie haben diese lediglich aus der Natur abstrahiert, in ein imaginäres Objekt umgewandelt und schließlich wieder als reales Objekt auf den Computer gebracht.

In der abstrakten Welt modellieren wir mehrere Fächer meist durch eine einfache Liste. Jeder Listeneintrag repräsentiert ein Fach, was wiederum eine Liste aber auch eine andere Sammlung (Collection) sein kann, siehe untere Abbildung 24.2.

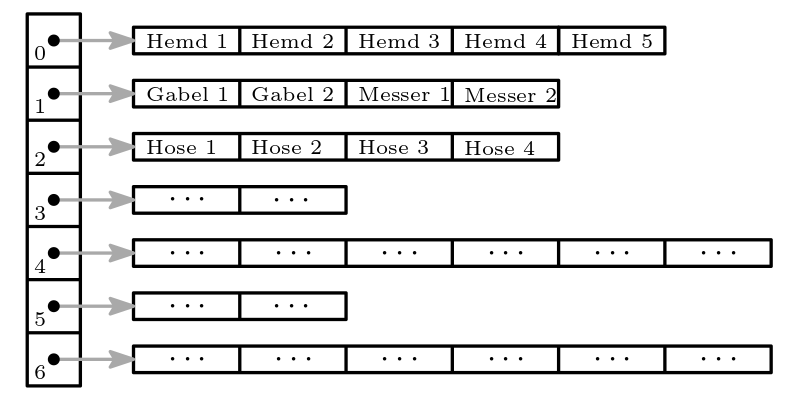
../../_images/bucket.png — Abb. 24.2 Fächer als Liste von Listen#

Da wir eine Liste zur Modellierung verwenden, müssen wir anhand des Listenindex das gewünschte Fach identifizieren können. In unserem Beispiel brauchen wir eine Funktion index_of die uns für einen Buchstaben den korrekten Index liefert.

def index_of(name):
    return ord(name[0]) - ord('A')

Wir machen aus unique_names_lex eine zweidimensionale Liste names_by_letter, sodass

names_by_letter[0] alle Namen die mit A beginnen enthält, und
names_by_letter[1] alle Namen die mit B beginnen enthält, und
…
names_by_letter[25] alle Namen die mit Z beginnen enthält.

../../_images/babynames.png — Abb. 24.3 Babynamen in Fächern#

Exercise 24.12 (Babynamen in Fächern)

Schreiben Sie eine Funktion to_lex_buckets(unique_names_lex) welche Ihnen die Sammlung aus Abbildung 24.3 erzeugt.

def to_lex_buckets(unique_names_lex):
    names_by_letter = [[]]
    letter = 'A'

    for name in unique_names_lex:
        while name[0] != letter:
            letter = chr(ord(letter)+1)
            names_by_letter.append([])     
        names_by_letter[index_of(letter)].append(name)
    return names_by_letter

names_by_letter = to_lex_buckets(unique_names_lex)

Beachten Sie, dass wir statt einer if-Kondition, eine while-Schleife verwenden. Warum? Nun es könnte sein, dass es einen Buchstaben gibt, für den gar kein Name in der Liste ist.

Um mit unserer neuen Datenstruktur zurecht zu kommen, können wir uns weitere Hilfsfunktionen basteln. Zum Beispiel wäre es praktisch auf ein bestimmtes Fach nicht über den Index 0,1,…, 25, sondern über den entsprechenden Buchstaben A,B,…,Z zuzugreifen.

Exercise 24.13 (Zugriff eines Fachs)

Schreiben Sie eine Funktion get_names(char, names_by_letter), die Ihnen für einen Buchstaben char die Liste mit allen Babynamen, welche mit char beginnen (der soeben erzeugen Datenstruktur names_by_letter) zurückliefert.

def get_names(char, names_by_letter):
    return names_by_letter[index_of(char)]

get_names('C', names_by_letter)

['Caddie',
 'Cade',
 'Caden',
 'Cadence',
 'Cael',
 'Caesar',
 'Caiden',
 'Cailyn',
 'Cain',
 'Caitlin',
 'Caitlyn',
 'Caitlynn',
 'Cal',
 'Caldonia',
 'Cale',
 'Caleb',
 'Caleigh',
 'Calhoun',
 'Cali',
 'Calista',
 'Calla',
 'Callie',
 'Callum',
 'Calvin',
 'Cam',
 'Camden',
 'Cameron',
 'Cami',
 'Camila',
 'Camilla',
 'Camille',
 'Camisha',
 'Cammie',
 'Campbell',
 'Camren',
 'Camron',
 'Camryn',
 'Candace',
 'Candi',
 'Candice',
 'Candida',
 'Candido',
 'Candis',
 'Candy',
 'Candyce',
 'Cannie',
 'Cannon',
 'Canyon',
 'Cap',
 'Capitola',
 'Cappie',
 'Caprice',
 'Captain',
 'Cara',
 'Caren',
 'Carey',
 'Cari',
 'Carie',
 'Carin',
 'Carina',
 'Carisa',
 'Carissa',
 'Carl',
 'Carla',
 'Carlee',
 'Carleen',
 'Carleigh',
 'Carlene',
 'Carleton',
 'Carley',
 'Carli',
 'Carlie',
 'Carlisle',
 'Carlo',
 'Carlos',
 'Carlota',
 'Carlotta',
 'Carlton',
 'Carly',
 'Carlyle',
 'Carlyn',
 'Carma',
 'Carmel',
 'Carmela',
 'Carmelita',
 'Carmella',
 'Carmelo',
 'Carmen',
 'Carmine',
 'Carnell',
 'Caro',
 'Carol',
 'Carolann',
 'Carole',
 'Carolee',
 'Carolina',
 'Caroline',
 'Carolyn',
 'Carolyne',
 'Carolynn',
 'Caron',
 'Carra',
 'Carri',
 'Carrie',
 'Carrol',
 'Carroll',
 'Carry',
 'Carsen',
 'Carson',
 'Carter',
 'Cary',
 'Caryl',
 'Caryn',
 'Cas',
 'Casandra',
 'Case',
 'Casey',
 'Cash',
 'Casie',
 'Casimer',
 'Casimir',
 'Casimiro',
 'Cason',
 'Casper',
 'Cass',
 'Cassandra',
 'Cassidy',
 'Cassie',
 'Cassius',
 'Cassondra',
 'Caswell',
 'Catalina',
 'Catharine',
 'Catherine',
 'Cathern',
 'Cathey',
 'Cathi',
 'Cathie',
 'Cathleen',
 'Cathrine',
 'Cathryn',
 'Cathy',
 'Catina',
 'Cato',
 'Catrina',
 'Cayden',
 'Cayla',
 'Caylee',
 'Ceasar',
 'Cecelia',
 'Cecil',
 'Cecile',
 'Cecilia',
 'Cecily',
 'Cedric',
 'Cedrick',
 'Ceil',
 'Celena',
 'Celesta',
 'Celeste',
 'Celestia',
 'Celestine',
 'Celestino',
 'Celia',
 'Celie',
 'Celina',
 'Celine',
 'Cena',
 'Ceola',
 'Cephus',
 'Cesar',
 'Ceylon',
 'Chace',
 'Chad',
 'Chadd',
 'Chadrick',
 'Chadwick',
 'Chaim',
 'Chaka',
 'Chalmer',
 'Chalmers',
 'Champ',
 'Chana',
 'Chance',
 'Chancey',
 'Chancy',
 'Chanda',
 'Chandler',
 'Chandra',
 'Chanel',
 'Chanelle',
 'Chaney',
 'Chanie',
 'Channie',
 'Channing',
 'Chantal',
 'Chante',
 'Chantel',
 'Chantelle',
 'Charissa',
 'Charisse',
 'Charity',
 'Charla',
 'Charle',
 'Charlee',
 'Charleen',
 'Charlene',
 'Charles',
 'Charley',
 'Charlie',
 'Charline',
 'Charlize',
 'Charlotta',
 'Charlotte',
 'Charlottie',
 'Charls',
 'Charlsie',
 'Charlton',
 'Charly',
 'Charmaine',
 'Charolette',
 'Chas',
 'Chase',
 'Chasity',
 'Chastity',
 'Chauncey',
 'Chauncy',
 'Chaya',
 'Chaz',
 'Che',
 'Chelsea',
 'Chelsey',
 'Chelsi',
 'Chelsie',
 'Chelsy',
 'Cher',
 'Cherelle',
 'Cheri',
 'Cherie',
 'Cherilyn',
 'Cherise',
 'Cherish',
 'Cherrelle',
 'Cherri',
 'Cherrie',
 'Cherry',
 'Cherryl',
 'Cheryl',
 'Cheryle',
 'Cheryll',
 'Chesley',
 'Chessie',
 'Chester',
 'Chestina',
 'Chet',
 'Cheyanne',
 'Cheyenne',
 'Chimere',
 'Chin',
 'China',
 'Chip',
 'Chiquita',
 'Chloe',
 'Chloie',
 'Chris',
 'Chrissie',
 'Chrissy',
 'Christ',
 'Christa',
 'Christal',
 'Christeen',
 'Christel',
 'Christen',
 'Christena',
 'Christene',
 'Christi',
 'Christian',
 'Christiana',
 'Christie',
 'Christin',
 'Christina',
 'Christine',
 'Christion',
 'Christop',
 'Christoper',
 'Christopher',
 'Christy',
 'Chrystal',
 'Chuck',
 'Chyna',
 'Chynna',
 'Ciara',
 'Ciarra',
 'Cicely',
 'Cicero',
 'Cielo',
 'Ciera',
 'Cierra',
 'Ciji',
 'Cilla',
 'Cinda',
 'Cindi',
 'Cindy',
 'Cinnamon',
 'Cinthia',
 'Citlali',
 'Citlalli',
 'Clabe',
 'Claiborne',
 'Clair',
 'Claire',
 'Clara',
 'Clarabelle',
 'Clarance',
 'Clare',
 'Clarence',
 'Claribel',
 'Clarice',
 'Clarinda',
 'Clarine',
 'Clarisa',
 'Clarissa',
 'Clark',
 'Clarke',
 'Clarnce',
 'Classie',
 'Claud',
 'Claude',
 'Claudette',
 'Claudia',
 'Claudie',
 'Claudine',
 'Claudio',
 'Claudius',
 'Claus',
 'Clay',
 'Clayton',
 'Clearence',
 'Cleave',
 'Cleda',
 'Clell',
 'Clella',
 'Clem',
 'Clemence',
 'Clemens',
 'Clement',
 'Clemente',
 'Clementina',
 'Clementine',
 'Clemie',
 'Clemma',
 'Clemmie',
 'Clemon',
 'Cleo',
 'Cleola',
 'Cleon',
 'Cleone',
 'Cleora',
 'Cleta',
 'Cletus',
 'Cleva',
 'Cleve',
 'Cleveland',
 'Clevie',
 'Clide',
 'Cliff',
 'Cliffie',
 'Clifford',
 'Clifton',
 'Clint',
 'Clinton',
 'Clive',
 'Cloe',
 'Clora',
 'Clotilda',
 'Clotilde',
 'Clovis',
 'Cloyd',
 'Clyda',
 'Clyde',
 'Clydie',
 'Clytie',
 'Coby',
 'Codey',
 'Codi',
 'Codie',
 'Cody',
 'Coen',
 'Cohen',
 'Colbert',
 'Colby',
 'Cole',
 'Coleen',
 'Coleman',
 'Coleton',
 'Coletta',
 'Colette',
 'Coley',
 'Colie',
 'Colin',
 'Colleen',
 'Collette',
 'Collie',
 'Collier',
 'Collin',
 'Collins',
 'Collis',
 'Colon',
 'Colonel',
 'Colt',
 'Colten',
 'Colter',
 'Colton',
 'Columbia',
 'Columbus',
 'Colvin',
 'Commodore',
 'Con',
 'Conard',
 'Concepcion',
 'Concetta',
 'Concha',
 'Conley',
 'Conner',
 'Connie',
 'Connor',
 'Conor',
 'Conrad',
 'Constance',
 'Constantine',
 'Consuela',
 'Consuelo',
 'Contina',
 'Conway',
 'Coolidge',
 'Cooper',
 'Cora',
 'Coraima',
 'Coral',
 'Coralie',
 'Corbett',
 'Corbin',
 'Corda',
 'Cordaro',
 'Cordelia',
 'Cordell',
 'Cordella',
 'Cordero',
 'Cordia',
 'Cordie',
 'Corean',
 'Corene',
 'Coretta',
 'Corey',
 'Cori',
 'Corie',
 'Corina',
 'Corine',
 'Corinna',
 'Corinne',
 'Corliss',
 'Cornel',
 'Cornelia',
 'Cornelious',
 'Cornelius',
 'Cornell',
 'Cornie',
 'Corrie',
 'Corrina',
 'Corrine',
 'Corry',
 'Cortez',
 'Cortney',
 'Corwin',
 'Cory',
 'Cosmo',
 'Coty',
 'Council',
 'Courtland',
 'Courtney',
 'Coy',
 'Craig',
 'Crawford',
 'Creed',
 'Creola',
 'Cressie',
 'Crete',
 'Cris',
 'Crissie',
 'Crissy',
 'Crista',
 'Cristal',
 'Cristen',
 'Cristi',
 'Cristian',
 'Cristin',
 'Cristina',
 'Cristine',
 'Cristobal',
 'Cristofer',
 'Cristopher',
 'Cristy',
 'Crockett',
 'Cruz',
 'Crysta',
 'Crystal',
 'Cuba',
 'Cullen',
 'Curley',
 'Curt',
 'Curtis',
 'Curtiss',
 'Cydney',
 'Cyndi',
 'Cyntha',
 'Cynthia',
 'Cyril',
 'Cyrus']

24.2.4. Ordnung durch Markierungen#

Wenn wir ein Telefonbuch genauer betrachten werden wir feststellen, dass es mit gut sichtbaren Markierungen versehen ist. Zum Beispiel finden wir häufig für jeden Anfangsbuchstaben eine solche Markierung. Wir können diese Markierungen auch als Fächer interpretieren, denn mithilfe von zwei aufeinanderfolgenden Markierungen beschreiben wir ein Fach. Nehmen wir zum Beispiel die Markierung für C und D, so können wir das Fach C bzw. mit dem Index 2 identifizieren.

Diese Gemeinsamkeit ist ersichtlich doch worin unterscheiden sich Markierungen von Fächern? Anders gefragt: Worin unterscheidet sich Ihr Kleiderschrank von einem Telefonbuch im wesentlichen?

Exercise 24.14 (Kleiderschrank und Telefonbücher)

Welche wesentliche Eigenschaft unterscheidet einen Kleiderschrank (Fächer) von einem Telefonbuch (Markierungen)?

Hinweis: Es geht uns um eine Eigenschaft, die sich auf die Implementierung auswirken wird.

Solution to Exercise 24.14 (Kleiderschrank und Telefonbücher)

Einen Kleiderschrank können wir jederzeit befüllen und leeren, er ist veränderlich (engl. mutable)! Wir legen neue Kleider hinein und holen Kleider heraus.

Ein Telefonbuch ist in der Regel unveränderlich (engl. immutable).

Wenn Sie sich unsere Implementierung der Fächer ansehen, wird klar, dass wir sehr einfach neue Namen hinzufügen können. Falls uns doppelte Elemente und die Sortierung innerhalb eines Fachs gleichgültig sind, reicht es das Element hinten anzuhängen. Andernfalls müssen wir die richtige Stelle identifizieren an der wir ein neues Element einfügen wollen. Wir müssen in jedem Fall nichts an der Anordnung der Fächer ändern!

Wie realisieren wir Markierungen? Eine Markierung zeigt auf eine bestimmte Seite im Telefonbuch. Im Beispiel mit den Babynamen, zeigt sie auf einen bestimmten Index der Liste aus Babynamen. Wir verwenden weiterhin unique_names_lex, fügen aber eine weitere unterstützende Liste marks hinzu, sodass

marks[0] ist der kleinste Index der Indices der Wörter die mit einem A beginnen,
marks[1] ist der kleinste Index der Indices der Wörter die mit einem B beginnen,
…
marks[25] ist der kleinste Index der Indices der Wörter die mit einem Z beginnen,

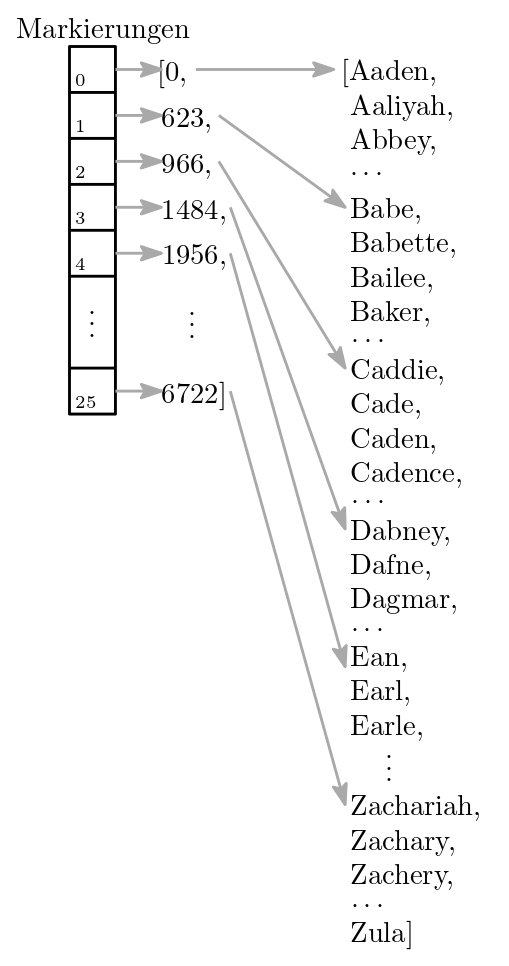
../../_images/marks.png — Abb. 24.4 Babynamen (rechts) mit Markierungen (links)#

Exercise 24.15 (Markierungen erzeugen)

Schreiben Sie eine Funktion generate_marks(names_by_letter) die Ihnen die Markierungen marks aus Abbildung 24.4 erzeugt.

def generate_marks(names_by_letter):
    marks = [0]
    letter = 'A'
    index = 0
    for name in unique_names_lex:
        while name[0] != letter:
            letter = chr(ord(letter)+1)
            marks.append(index)
        index += 1
    return marks

marks = generate_marks(unique_names_lex)
unique_names_lex[marks[1]-1]

'Azzie'

Wir können nun sehr einfach durch alle Namen iterieren, die mit einem C starten:

marks = generate_marks(unique_names_lex)

mark_index = index_of('C')
for i in range(marks[mark_index], marks[mark_index+1]-1, 1):
    print(unique_names_lex[i])

Caddie
Cade
Caden
Cadence
Cael
Caesar
Caiden
Cailyn
Cain
Caitlin
Caitlyn
Caitlynn
Cal
Caldonia
Cale
Caleb
Caleigh
Calhoun
Cali
Calista
Calla
Callie
Callum
Calvin
Cam
Camden
Cameron
Cami
Camila
Camilla
Camille
Camisha
Cammie
Campbell
Camren
Camron
Camryn
Candace
Candi
Candice
Candida
Candido
Candis
Candy
Candyce
Cannie
Cannon
Canyon
Cap
Capitola
Cappie
Caprice
Captain
Cara
Caren
Carey
Cari
Carie
Carin
Carina
Carisa
Carissa
Carl
Carla
Carlee
Carleen
Carleigh
Carlene
Carleton
Carley
Carli
Carlie
Carlisle
Carlo
Carlos
Carlota
Carlotta
Carlton
Carly
Carlyle
Carlyn
Carma
Carmel
Carmela
Carmelita
Carmella
Carmelo
Carmen
Carmine
Carnell
Caro
Carol
Carolann
Carole
Carolee
Carolina
Caroline
Carolyn
Carolyne
Carolynn
Caron
Carra
Carri
Carrie
Carrol
Carroll
Carry
Carsen
Carson
Carter
Cary
Caryl
Caryn
Cas
Casandra
Case
Casey
Cash
Casie
Casimer
Casimir
Casimiro
Cason
Casper
Cass
Cassandra
Cassidy
Cassie
Cassius
Cassondra
Caswell
Catalina
Catharine
Catherine
Cathern
Cathey
Cathi
Cathie
Cathleen
Cathrine
Cathryn
Cathy
Catina
Cato
Catrina
Cayden
Cayla
Caylee
Ceasar
Cecelia
Cecil
Cecile
Cecilia
Cecily
Cedric
Cedrick
Ceil
Celena
Celesta
Celeste
Celestia
Celestine
Celestino
Celia
Celie
Celina
Celine
Cena
Ceola
Cephus
Cesar
Ceylon
Chace
Chad
Chadd
Chadrick
Chadwick
Chaim
Chaka
Chalmer
Chalmers
Champ
Chana
Chance
Chancey
Chancy
Chanda
Chandler
Chandra
Chanel
Chanelle
Chaney
Chanie
Channie
Channing
Chantal
Chante
Chantel
Chantelle
Charissa
Charisse
Charity
Charla
Charle
Charlee
Charleen
Charlene
Charles
Charley
Charlie
Charline
Charlize
Charlotta
Charlotte
Charlottie
Charls
Charlsie
Charlton
Charly
Charmaine
Charolette
Chas
Chase
Chasity
Chastity
Chauncey
Chauncy
Chaya
Chaz
Che
Chelsea
Chelsey
Chelsi
Chelsie
Chelsy
Cher
Cherelle
Cheri
Cherie
Cherilyn
Cherise
Cherish
Cherrelle
Cherri
Cherrie
Cherry
Cherryl
Cheryl
Cheryle
Cheryll
Chesley
Chessie
Chester
Chestina
Chet
Cheyanne
Cheyenne
Chimere
Chin
China
Chip
Chiquita
Chloe
Chloie
Chris
Chrissie
Chrissy
Christ
Christa
Christal
Christeen
Christel
Christen
Christena
Christene
Christi
Christian
Christiana
Christie
Christin
Christina
Christine
Christion
Christop
Christoper
Christopher
Christy
Chrystal
Chuck
Chyna
Chynna
Ciara
Ciarra
Cicely
Cicero
Cielo
Ciera
Cierra
Ciji
Cilla
Cinda
Cindi
Cindy
Cinnamon
Cinthia
Citlali
Citlalli
Clabe
Claiborne
Clair
Claire
Clara
Clarabelle
Clarance
Clare
Clarence
Claribel
Clarice
Clarinda
Clarine
Clarisa
Clarissa
Clark
Clarke
Clarnce
Classie
Claud
Claude
Claudette
Claudia
Claudie
Claudine
Claudio
Claudius
Claus
Clay
Clayton
Clearence
Cleave
Cleda
Clell
Clella
Clem
Clemence
Clemens
Clement
Clemente
Clementina
Clementine
Clemie
Clemma
Clemmie
Clemon
Cleo
Cleola
Cleon
Cleone
Cleora
Cleta
Cletus
Cleva
Cleve
Cleveland
Clevie
Clide
Cliff
Cliffie
Clifford
Clifton
Clint
Clinton
Clive
Cloe
Clora
Clotilda
Clotilde
Clovis
Cloyd
Clyda
Clyde
Clydie
Clytie
Coby
Codey
Codi
Codie
Cody
Coen
Cohen
Colbert
Colby
Cole
Coleen
Coleman
Coleton
Coletta
Colette
Coley
Colie
Colin
Colleen
Collette
Collie
Collier
Collin
Collins
Collis
Colon
Colonel
Colt
Colten
Colter
Colton
Columbia
Columbus
Colvin
Commodore
Con
Conard
Concepcion
Concetta
Concha
Conley
Conner
Connie
Connor
Conor
Conrad
Constance
Constantine
Consuela
Consuelo
Contina
Conway
Coolidge
Cooper
Cora
Coraima
Coral
Coralie
Corbett
Corbin
Corda
Cordaro
Cordelia
Cordell
Cordella
Cordero
Cordia
Cordie
Corean
Corene
Coretta
Corey
Cori
Corie
Corina
Corine
Corinna
Corinne
Corliss
Cornel
Cornelia
Cornelious
Cornelius
Cornell
Cornie
Corrie
Corrina
Corrine
Corry
Cortez
Cortney
Corwin
Cory
Cosmo
Coty
Council
Courtland
Courtney
Coy
Craig
Crawford
Creed
Creola
Cressie
Crete
Cris
Crissie
Crissy
Crista
Cristal
Cristen
Cristi
Cristian
Cristin
Cristina
Cristine
Cristobal
Cristofer
Cristopher
Cristy
Crockett
Cruz
Crysta
Crystal
Cuba
Cullen
Curley
Curt
Curtis
Curtiss
Cydney
Cyndi
Cyntha
Cynthia
Cyril

Oder wir können uns eine Teilliste kopieren, die nur Namen beinhaltet die mit D starten:

mark_index = index_of('D')
unique_names_lex[marks[mark_index]:marks[mark_index+1]]

['Dabney',
 'Dafne',
 'Dagmar',
 'Dagny',
 'Dahlia',
 'Daija',
 'Daijah',
 'Daisey',
 'Daisha',
 'Daisie',
 'Daisy',
 'Daisye',
 'Daja',
 'Dakoda',
 'Dakota',
 'Dakotah',
 'Dale',
 'Dalia',
 'Dallas',
 'Dallin',
 'Dalton',
 'Dalvin',
 'Damarcus',
 'Damari',
 'Damarion',
 'Damaris',
 'Dameon',
 'Damian',
 'Damien',
 'Damion',
 'Damon',
 'Damond',
 'Dan',
 'Dana',
 'Danae',
 'Dandre',
 'Dane',
 'Daneen',
 'Danelle',
 'Danette',
 'Dangelo',
 'Dani',
 'Dania',
 'Danial',
 'Danica',
 'Daniel',
 'Daniela',
 'Daniele',
 'Daniella',
 'Danielle',
 'Danika',
 'Danita',
 'Dann',
 'Danna',
 'Dannie',
 'Danniel',
 'Dannielle',
 'Danny',
 'Dante',
 'Danyel',
 'Danyell',
 'Danyelle',
 'Daphne',
 'Daquan',
 'Dara',
 'Darby',
 'Darci',
 'Darcie',
 'Darcy',
 'Darell',
 'Daren',
 'Daria',
 'Darian',
 'Dariana',
 'Darien',
 'Darin',
 'Dario',
 'Darion',
 'Darius',
 'Darl',
 'Darla',
 'Darleen',
 'Darlene',
 'Darline',
 'Darlyne',
 'Darnell',
 'Darold',
 'Daron',
 'Darrel',
 'Darrell',
 'Darren',
 'Darrian',
 'Darrick',
 'Darrien',
 'Darrin',
 'Darrion',
 'Darrius',
 'Darron',
 'Darry',
 'Darryl',
 'Darryle',
 'Darryll',
 'Darryn',
 'Darvin',
 'Darwin',
 'Darwyn',
 'Daryl',
 'Daryle',
 'Daryn',
 'Dashawn',
 'Dasia',
 'Daulton',
 'Daunte',
 'Davante',
 'Dave',
 'Davey',
 'Davian',
 'David',
 'Davie',
 'Davin',
 'Davina',
 'Davion',
 'Davis',
 'Davon',
 'Davonta',
 'Davonte',
 'Davy',
 'Dawn',
 'Dawna',
 'Dawne',
 'Dawson',
 'Dax',
 'Daxton',
 'Dayami',
 'Dayana',
 'Dayanara',
 'Dayle',
 'Dayna',
 'Dayne',
 'Dayse',
 'Dayton',
 'Deacon',
 'Dean',
 'Deana',
 'Deandra',
 'Deandre',
 'Deane',
 'Deangelo',
 'Deann',
 'Deanna',
 'Deanne',
 'Deante',
 'Deasia',
 'Deb',
 'Debbi',
 'Debbie',
 'Debbra',
 'Debby',
 'Debera',
 'Debi',
 'Debora',
 'Deborah',
 'Deborrah',
 'Debra',
 'Debrah',
 'Debroah',
 'Declan',
 'Dedra',
 'Dedric',
 'Dedrick',
 'Dee',
 'Deeann',
 'Deedee',
 'Deegan',
 'Deena',
 'Deetta',
 'Deforest',
 'Deidra',
 'Deidre',
 'Deion',
 'Deirdre',
 'Deja',
 'Dejah',
 'Dejon',
 'Dejuan',
 'Del',
 'Delaney',
 'Delano',
 'Delbert',
 'Delcie',
 'Delfina',
 'Delia',
 'Deliah',
 'Delila',
 'Delilah',
 'Delina',
 'Delinda',
 'Delisa',
 'Dell',
 'Della',
 'Dellar',
 'Delle',
 'Dellia',
 'Dellie',
 'Delma',
 'Delmar',
 'Delmas',
 'Delmer',
 'Delmus',
 'Delois',
 'Delora',
 'Delores',
 'Deloris',
 'Delos',
 'Delpha',
 'Delphia',
 'Delphin',
 'Delphine',
 'Delsie',
 'Delta',
 'Delton',
 'Delvin',
 'Delwin',
 'Dema',
 'Demarco',
 'Demarcus',
 'Demario',
 'Demarion',
 'Demetra',
 'Demetri',
 'Demetria',
 'Demetric',
 'Demetrios',
 'Demetrius',
 'Demi',
 'Demian',
 'Demond',
 'Demonte',
 'Dempsey',
 'Dena',
 'Deneen',
 'Denese',
 'Denice',
 'Denine',
 'Denis',
 'Denise',
 'Denisha',
 'Denisse',
 'Denita',
 'Dennie',
 'Dennis',
 'Denny',
 'Denton',
 'Denver',
 'Denzel',
 'Denzell',
 'Denzil',
 'Deon',
 'Deondre',
 'Deonta',
 'Deontae',
 'Deonte',
 'Dequan',
 'Derald',
 'Dereck',
 'Derek',
 'Dereon',
 'Deric',
 'Derick',
 'Derik',
 'Derl',
 'Deron',
 'Derrek',
 'Derrell',
 'Derrick',
 'Derwin',
 'Deryl',
 'Desean',
 'Deshaun',
 'Deshawn',
 'Desi',
 'Desirae',
 'Desiree',
 'Desmond',
 'Dessa',
 'Dessie',
 'Destany',
 'Destin',
 'Destinee',
 'Destiney',
 'Destini',
 'Destiny',
 'Destry',
 'Devan',
 'Devante',
 'Devaughn',
 'Deven',
 'Devin',
 'Devon',
 'Devonta',
 'Devontae',
 'Devonte',
 'Devyn',
 'Deward',
 'Dewayne',
 'Dewey',
 'Dewitt',
 'Dexter',
 'Deyanira',
 'Dezzie',
 'Diallo',
 'Diamond',
 'Dian',
 'Diana',
 'Diandra',
 'Diane',
 'Diann',
 'Dianna',
 'Dianne',
 'Dicie',
 'Dick',
 'Dickie',
 'Dicy',
 'Diego',
 'Dijon',
 'Dillan',
 'Dillard',
 'Dillie',
 'Dillion',
 'Dillon',
 'Dimitri',
 'Dimitrios',
 'Dimple',
 'Dina',
 'Dinah',
 'Dink',
 'Dino',
 'Dion',
 'Dione',
 'Dionicio',
 'Dionne',
 'Dionte',
 'Dirk',
 'Dixie',
 'Dixon',
 'Diya',
 'Djuana',
 'Djuna',
 'Doc',
 'Docia',
 'Dock',
 'Doctor',
 'Dola',
 'Doll',
 'Dollie',
 'Dolly',
 'Dollye',
 'Dolores',
 'Doloris',
 'Dolph',
 'Dolphus',
 'Domenic',
 'Domenica',
 'Domenick',
 'Domenico',
 'Dominga',
 'Domingo',
 'Dominic',
 'Dominick',
 'Dominik',
 'Dominique',
 'Dominque',
 'Domonique',
 'Don',
 'Dona',
 'Donaciano',
 'Donal',
 'Donald',
 'Donat',
 'Donato',
 'Donavan',
 'Donavon',
 'Dondre',
 'Donell',
 'Donia',
 'Donie',
 'Donita',
 'Donn',
 'Donna',
 'Donnell',
 'Donnie',
 'Donny',
 'Donovan',
 'Donta',
 'Dontae',
 'Donte',
 'Dora',
 'Dorathea',
 'Dorathy',
 'Dorcas',
 'Doreen',
 'Dorene',
 'Doretha',
 'Doretta',
 'Dori',
 'Dorian',
 'Dorinda',
 'Dorine',
 'Doris',
 'Dorla',
 'Dorman',
 'Dorotha',
 'Dorothea',
 'Dorothy',
 'Dorr',
 'Dorris',
 'Dorsey',
 'Dortha',
 'Dorthea',
 'Dorthey',
 'Dorthy',
 'Dosha',
 'Doshia',
 'Doshie',
 'Dosia',
 'Doss',
 'Dossie',
 'Dot',
 'Dottie',
 'Dotty',
 'Doug',
 'Douglas',
 'Douglass',
 'Dove',
 'Dovie',
 'Dow',
 'Doyle',
 'Dozier',
 'Drake',
 'Draven',
 'Drema',
 'Drew',
 'Drucilla',
 'Drury',
 'Drusilla',
 'Duane',
 'Duard',
 'Dudley',
 'Duff',
 'Duke',
 'Dulce',
 'Dulcie',
 'Duncan',
 'Durell',
 'Durrell',
 'Durward',
 'Durwood',
 'Dustan',
 'Dustin',
 'Dusty',
 'Duwayne',
 'Dwain',
 'Dwaine',
 'Dwan',
 'Dwane',
 'Dwayne',
 'Dwight',
 'Dwyane',
 'Dyan',
 'Dylan',
 'Dyllan',
 'Dylon']

Wir hatten festgehalten, dass sich ein Telefonbuch mit Markierungen nicht verändert. Welches Problem tritt auf wenn wir Elemente in die Liste der sortierten Babynamen einfügen?

Exercise 24.16 (Elemente einfügen und Markierungen anpassen)

Schreiben Sie folgende Hilfsfunktionen:

add_name(name, unique_names_lex, marks): Fügt einen Namen name an die korrekte Stelle in unique_names_lex ein.
remove_name_(name, unique_names_lex, marks): Löscht einen Namen name (falls vorhanden).

Beide Funktionen passen marks entsprechend an! Die Sortierung soll erhalten bleiben! Eventuell macht es Sinn eine weitere Hilfsfunktion index_of_element(name, unique_names_lex, marks) zu schreiben, welche Ihnen den Index i des Namen name in unique_names_lex zurückliefert.

Tipp: Verwenden Sie die Methoden der Python-Liste append, insert und pop.

def index_of_element(name, unique_names_lex, marks):
    if name < unique_names_lex[0]:
        return 0
    
    if name > unique_names_lex[len(unique_names_lex)-1]:
        return len(unique_names_lex)
    
    letter = name[0]
    mark_index = ord(letter)-ord("A")
    start = marks[mark_index]
    end = marks[mark_index+1]
    
    for i in range(start, end, 1):
        if unique_names_lex[i] == name:
            return i
        if unique_names_lex[i] > name:
            if unique_names_lex[i-1] < name:
                return i-1
            
def add_element(name, unique_names_lex, marks):
    # 1. compute index
    index = index_of_element(name, unique_names_lex, marks)

    # 2. insert if name is not contained
    if unique_names_lex[index] != name:
        unique_names_lex.insert(index, name)
       
        # 3. adapt marks
        letter = name[0]
        mark_index = ord(letter)-ord("A")
        for i in range(mark_index+1, len(marks), 1):
            marks[i] +=1
        return True
    return False
    
def remove_element(name, unique_names_lex, marks):
    # 1. compute index
    index = index_of_element(name, unique_names_lex, marks)
    
    # 2. delete if name is contained
    if unique_names_lex[index] == name:
        unique_names_lex.pop(index)
        
        # 3. adapt marks
        letter = name[0]
        mark_index = ord(letter)-ord("A")
        for i in range(mark_index+1, len(marks), 1):
            marks[i] -=1
        return True
    return False
        
print(index_of_element(unique_names_lex[88], unique_names_lex, marks) == 88)
print(index_of_element(unique_names_lex[2388], unique_names_lex, marks) == 2388)
name = "Mustermann"
print(len(unique_names_lex))
add_element(name, unique_names_lex, marks)
print(len(unique_names_lex))
remove_element(name, unique_names_lex, marks)
print(len(unique_names_lex))

True
True
6782
6783
6782

Immer wenn wir die Liste mit sortierten Babynamen ändern, müssen wir auch marks anpassen. Je nachdem wie viele Markierungen wir haben, kann dies viel Zeit kosten.

24.3. Hashing und das Dictionary#

In Speicher - alles ist eine Liste haben wir uns angesehen wie Listen im Arbeitsspeicher realisiert werden. Erinnern Sie sich! Im Speicher liegen nur Zahlen und aus diesen Zahlen haben wir uns den Datentyp Liste gebastelt.

Was wir nicht beschrieben haben ist wie die zweite wesentliche Datenstruktur, das Dictionary im Speicher realisiert ist. Wie der Titel dieser Aufgabe betont, ist alles eine Liste. Der Arbeitsspeicher ist eine Liste durch den wir Python-Listen erhalten und die Basis des Dictionary ist Liste die im Speicher liegt.

In diesem Abschnitt werden wir uns gemeinsam erarbeiten wie wir von einer Liste zu einem Wörterbuch/Dictionary gelangen. Der Schlüssel hierfür sind die sogenannten Hashingverfahren.

Datenstrukturen die das Hashing verwenden versuchen die Speicheradresse (siehe Speicher - alles ist eine Liste) bzw. den Index eines Elements in einer Liste direkt durch einfache arithmetische Operationen aus einem Schlüssel key des Elements zu berechnen. Genau genommen verwendet unsere obige Fächer-Datenstruktur ein einfache Hashfunktion, denn wir berechnen anhand des Anfangsbuchstaben eines Elements (d.h. seinem key) einen Index.

Mit ‚versuchen‘ meinen wir, dass zwei unterschiedliche Elemente mit unterschiedlichen Schlüsseln durchaus den gleichen Index ergeben können. Dies bezeichnen wir als Kollision. Diese Kollisionen müssen wir irgendwie auflösen und wir hoffen, dass wir möglichst weniger solcher Kollisionen erzeugen.

Universum, Schlüssel, Liste und Hashfunktion

Für die weitere Diskussion benötigen wir folgende Definitionen:

Ein Universum \(\mathcal{U}\) an möglichen Schlüsseln, zum Beispiel \(\mathcal{U} \subseteq \mathbb{N}_0\),
eine Menge an Schlüsseln \(\mathcal{K} \subseteq \mathcal{U}\),
eine Liste \(\mathcal{L}\) mit \(|\mathcal{L}| = n\), oft auch Hashtabelle genannt, und
eine Hashfunktion \(h : \mathcal{U} \rightarrow \{0, \ldots, n-1\}\)

In unserer Fächer-Datenstruktur, lösen wir Kollisionen auf indem wir alle Elemente mit gleichem Index in eine zweite Liste packen. Ein solches Verfahren heißt offenes Hashing mit geschlossener Adressierung.

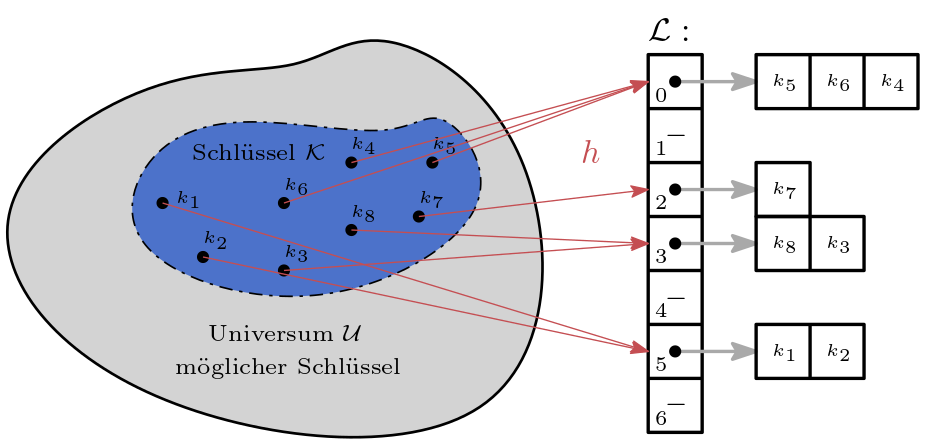
../../_images/open-hashing.png — Abb. 24.5 Offenes Hashing realisiert durch Fächer.#

Exercise 24.17 (Offenes Hashing)

Benennen Sie \(\mathcal{U}\), \(\mathcal{K}\), \(n\) unserer Fächer-Datenstruktur und beschreiben Sie \(h\).

Solution to Exercise 24.17 (Offenes Hashing)

\(\mathcal{U}\) = alle möglichen Zeichenketten
\(\mathcal{K}\) = alle Zeichenketten in unique_names_lex
\(n = 26\)
\(h\): Entspricht index_of(name) und berechnet aus dem ersten Zeichen einer Zeichenkette die Stelle des Buchstabens im Alphabet (beginnend bei Null).

Eine weitere Möglichkeit eine Kollision aufzulösen ist es nur eine große Liste zu verwenden. Tritt eine Kollision auf, so wird nach einem anderen freien Platz gesucht. Für diese Technik muss \(\mathcal{L}\) deutlich größer sein. Sobald die Liste droht voll zu laufen muss sie vergrößert werden.

Ein solches Verfahren heißt geschlossenes Hashing mit offener Adressierung. In Abbildung 24.6 ist dieses mit einer der einfachsten Kollisionsauflösungen skizziert: Falls ein Platz belegt ist suchen wir aufsteigend nach dem nächst liegenden freien Platz.

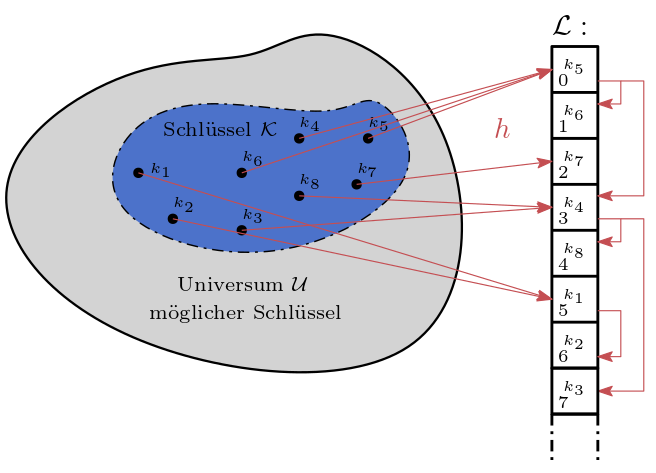
../../_images/closed-hashing.png — Abb. 24.6 Geschlossenes Hashing#

Egal welche Technik verwendet wird, eine solche Sammlung enthält keine doppelten Schlüssel. Wir nennen eine solche Sammlung auch Hashtable. Ziel ist es in konstant vielen Schritten \((\mathcal{O}(1))\) auf ein beliebiges Element einer solchen Sammlung

zuzugreifen search,
ein Element einzufügen insert,
oder zu löschen delete.

24.3.1. Geschlossenes Hashing#

Lassen Sie uns anstatt des offenen Hashings das geschlossene Hashing aus Abbildung 24.6 verwenden. Wir möchten dabei zunächst unsere bereits bekannte Hashfunktion index_of(name) einsetzten. Außerdem gehen wir zunächst davon aus, dass die Menge der Schlüssel erneut unsere Babynamen sind.

Exercise 24.18 (Indexsuche)

Schreiben Sie eine Funktion search_index(name, hashtable), welche Ihnen den index des Namens name der Liste hashtable anhand der Hashfunktion index_of(element) liefert. Gehen Sie davon aus, dass ein Platz in der Liste frei ist wenn dieser gleich None ist.

def search_index(name, hashtable):
    key = name
    index = index_of(key) % len(hashtable)
    for i in range(len(hashtable)):
        j = (index+i) % len(hashtable)
        if hashtable[j] == key:
            return j
        if hashtable[j] == None:
            return j
    
    # there is no free place left
    return None

Wir starten die Suche bei Index index_of(key) % len(hashtable) um sicher zu gehen, dass der Index nicht außerhalb der Liste liegt. Dann durchlaufen wir die Liste zyklisch bis wir einen freien Platz finden oder aber festellen, dass die Liste voll ist.

Exercise 24.19 (Hashtableverwaltung)

Schreiben Sie mithilfe search_index(name, hashtable) nun folgende Funktionen:

contains(name, hashtable): Liefert True genau dann wenn name sich in der Liste hashtable befindet.
get_value(name, hashtable): Liefert name zurück falls es in hashtable enthalten ist, sonst None.
insert(name, hashtable): Fügt name in hashtable falls es noch nicht in hashtable enthalten ist und gibt True zurück genau dann wenn name eingefügt wurde.
new_hash_table(names): Erzeugt unter der Verwendung der Funktion insert eine neue Liste hashtable welche alle Namen in der Liste names enthält.

Testen Sie Ihre Funktionen mithilfe einer kleinen Liste an Namen, z.B.

names = ['Berta', 'Hans', 'Thomas']

Hinweis: Überlegen Sie sich was Sie machen wenn die Liste voll gelaufen ist!

Falls hashtable voll ist fügen wir den einzufügenden Namen hinten an.

def index_of(name):
    return ord('A')-ord(name[0])

def search_index(name, hashtable):
    key = name
    index = index_of(key) % len(hashtable)
    for i in range(len(hashtable)):
        j = (index+i) % len(hashtable)
        if hashtable[j] == key:
            return j
        if hashtable[j] == None:
            return j
        
    # there is no free place left
    return len(hashtable)

def contains(name, hashtable):
    index = search_index(name, hashtable)
    return index < len(hashtable) and hashtable[index] == name

def get_value(name, hashtable):
    index = search_index(name, hashtable)
    if index < len(hashtable) and hashtable[index] == name:
        return hashtable[index]
    else:
        None

def insert(name, hashtable):
    index = search_index(name, hashtable)
    while index >= len(hashtable):
        hashtable.append(None)
        
    if hashtable[index] == name:
        return False
    else:
        hashtable[index] = name
        return True

def new_hash_table(names):
    hashtable = [None for i in range(2*len(names) + 8)]
    for name in names:
        insert(name, hashtable)
    return hashtable

Lassen Sie uns die Funktionen testen:

names = ['Berta', 'Hans', 'Thomas']
hashtable = new_hash_table(names)
print(f"hashtable = {hashtable}")
print(f"contains('Dieter', hashtable) = {contains('Dieter', hashtable)}") # False
print(f"contains('Berta', hashtable) = {contains('Berta', hashtable)}") # True
print(f"search_index('Dieter', hashtable) = {search_index('Dieter', hashtable)}") # 11
print(f"search_index('Berta', hashtable) = {search_index('Berta', hashtable)}") # 13
print(f"insert('Dieter', hashtable) = {insert('Dieter', hashtable)}") # True
print(f"insert('Dieter', hashtable) = {insert('Dieter', hashtable)}") # False

# fill the list to test if everything works if it is full
for name in unique_names_lex[0:20]:
    insert(name, hashtable)
    
print(f"hashtable = {hashtable}")

all([search_index(name, hashtable) == index for index, name in enumerate(hashtable)])

hashtable = [None, None, None, None, None, None, None, 'Hans', None, 'Thomas', None, None, None, 'Berta']
contains('Dieter', hashtable) = False
contains('Berta', hashtable) = True
search_index('Dieter', hashtable) = 11
search_index('Berta', hashtable) = 13
insert('Dieter', hashtable) = True
insert('Dieter', hashtable) = False
hashtable = ['Aaden', 'Aaliyah', 'Aarav', 'Aaron', 'Ab', 'Abagail', 'Abb', 'Hans', 'Abbey', 'Thomas', 'Abbie', 'Dieter', 'Abbigail', 'Berta', 'Abbott', 'Abby', 'Abdiel', 'Abdul', 'Abdullah', 'Abe', 'Abel', 'Abelardo', 'Abie', 'Abigail']

True

Die letzte Zeile des Codes erzeugt eine Liste aus boolschen Werten und wertet diese durch all aus. all ergibt genau dann True wenn jeder Wert in der Liste True ist. Der Wert am Index index ist True genau dann wenn der search_index(name, hashtable) = index, wobei name am Index index der Liste hashtable steht.

Was noch fehlt ist das Löschen eines Elements in unserer Hashtable. Für das offene Hashing ist dies recht einfach: Wir suchen das Fach und löschen das Element aus diesem heraus. Für das geschlossenes Hashing ist dies jedoch nicht so einfach! Angenommen wir fügen die Schlüssel 'Anna', 'Alex', 'Clara', 'Alba' und 'Fabian' nacheinander in eine leere Hashtabelle ein. Und angenommen wir verwenden als Hashfunktion index_of und eine lineare Sondierung. Dann erhalten wir als Resultat die Liste aus Abbildung 24.7.

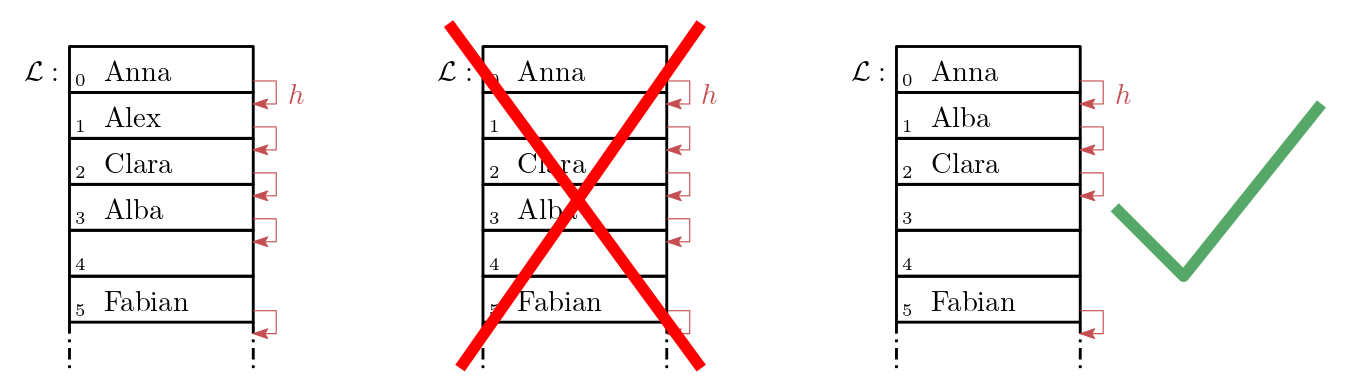
../../_images/closed-hashing-deletion.png — Abb. 24.7 Löschvorgang beim geschlossenes Hashing mit linearer Sondierung: Es wird der Schlüssel `'Alex'` gelöscht.#

Wenn wir nun 'Alex' einfach löschen und anschließend nach 'Alba' suchen, werden wir beim Index 1 stoppen und diesen Namen nicht mehr finden! Löschen wir 'Alex', so müssen wir alle Namen die einen größeren Index als 'Alex' haben und lückenlos aufeinander folgen, ebenfalls löschen und erneut einfügen. Beachten Sie, dass sich die Position von 'Clare' in der Liste in Abbildung 24.7 nicht verändert, da index_of('Clare') == 2.

Exercise 24.20 (Schlüssel löschen)

Implementieren Sie den beschriebenen Algorithmus zum löschen eines Schlüssels in der Hashtabelle, d.h., implementieren Sie die Funktion delete(name, hashtable).

def delete(name, hashtable):
    index = search_index(name, hashtable)
    if index < len(hashtable) and hashtable[index] == name:
        hashtable[index] = None
        i = 1
        while(hashtable[index+i] != None):
            value = hashtable[index+i]
            hashtable[index+i] = None
            insert(value, hashtable)
            i += 1
        return True
    else:
        return False

Lassen Sie uns das Beispiel aus Abbildung 24.7 testen:

names = ['Anna', 'Alex', 'Clara', 'Alba', 'Fabian']
hashtable = new_hash_table(names)
print(hashtable)
delete('Alex', hashtable)
print(hashtable)

['Anna', 'Alex', 'Alba', None, None, None, None, None, None, None, None, None, None, 'Fabian', None, None, 'Clara', None]
['Anna', 'Alba', None, None, None, None, None, None, None, None, None, None, None, 'Fabian', None, None, 'Clara', None]

Nun wird es Zeit unsere Hashtabelle mit den Babynamen aus unique_names_lex zu befüllen.

Exercise 24.21 (Hashtable füllen)

Füllen Sie nun eine neue hashtable mit den Namen aus unique_names_lex. Achten Sie auf die Zeit die dieser Vorgang in Anspruch nimmt. Was fällt Ihnen auf? Finden Sie eine Erklärung.

hashtable = new_hash_table(unique_names_lex)

Solution to Exercise 24.21 (Hashtable füllen)

Der Vorgang nimmt eine beachtliche Zeit in Anspruch. unique_names_lex enthält 6782 Namen. Unsere Hashfunktion liefert jedoch nur Werte zwischen 0 und 25. Damit iterieren wir für das Einfügen des \(m\)-ten Elements über mindestens \(m-25\) Elemente. Insgesamt benötigen wir damit in etwa

\[ \sum_{i=1}^n i = \frac{n \cdot (n+1)}{2} \]

also

\[ 6782 \cdot 6783 / 2 \approx 23 \cdot 10^6, \]

d.h., circa 23 Millionen Schritte! In anderen Worten wir haben immens viele Kollisionen. Unsere Hashfunktion index_of ist keine gute Hashfunktion!

24.3.2. Hashfunktionen#

Was genau ist eine Hashfunktion und wozu ist diese gut?

Hashfunktion

Eine Hashfunktion über einem Universum \(\mathcal{U}\) (zum Beispiel die Menge aller Zeichenketten)

\[h : \mathcal{U} \rightarrow \{0, \ldots, n\}\]

erzeugt durch meist einfache arithmetische Berechnungen aus einem Schlüssel \(k \in \mathcal{K} \subseteq \mathcal{U}\) eine natürliche Zahl h(k), sodass

(24.5)#\[k_i = k_j \Rightarrow h(k_i) = h(k_j).\]

Den Wert \(h(k)\) nennen wir Hashwert oder kurz Hash von \(k\).

Sind zwei Schlüssel verschieden muss die Hashfunktion hingegen keine verschiedenen Zahlen zurückliefern! Die einfachste gültige und zugleich recht nutzlose Hashfunktion ist eine Konstante, z.B., \(h(k) = 0\).

Hashfunktionen werden oft verwendet um zu prüfen ob zwei Schlüssel gleich sind. Aus Gleichung (24.5) folgt:

(24.6)#\[h(k_i) \neq h(k_j) \Rightarrow k_i \neq k_j.\]

Deshalb wertet man erst die Hashfunktion der beiden Schlüssel aus. Erst wenn die Hashfunktion die gleichen Werte liefert, prüft man genauer weiter. Da die Hashfunktion oft sehr schnell ausgewertet werden kann, insbesondere wenn

die Ungleichheit wahrscheinlich ist und
wir eine gute Hashfunktion besitzen

sind enorme Ersparnisse der Rechenzeit möglich. Sie können, zum Beispiel, aus einem riesigen Textdokument einen Hashwert generieren und so zwei Textdokumente auf Gleichheit prüfen.

Was aber ist eine gute Hashfunktion?

Die erste wichtige Eigenschaft einer guten Hashfunktion \(h\) ist, dass diese gut streut. D.h., werten wir alle Hashwerte für unsere Schlüssel \(\mathcal{K}\) aus, dann wäre es optimal, wenn jeder Hashwert eindeutig ist, d.h. wenn

\[ k_i \neq k_j \Rightarrow h(k_i) \neq h(k_j) \]

gilt. Ist der Hashwert nahezu zufällig gleichverteilt zwischen \(0\) und \(n-1\) ist dies ebenfalls eine sehr gute Hashfunktion.

Leider ist das Universum \(\mathcal{U}\) meistens riesig, insbesondere deutlich größer als die Hashtabelle \(\mathcal{L}\). Kennen wir \(\mathcal{K}\) im Voraus und ändert sich diese Menge nicht, dann lässt sich oft eine perfekte Hashfunktion berechnen. Ein Beispiel sind unsere oben besprochenen Markierungen.

Ein Geburtsdatum oder der Fingerabdruck (in einer Zahl codiert) wären Hashwert einer Person aus dem echten Leben. Das Geburtsdatum wäre jedoch ein schlechter Hashwert, da er für sehr viele Menschen gleich ist. Der Fingerabdruck hingegen ist ein sehr guter Hashwert.

Die zweite wichtige Eigenschaft einer guten Hashfunktion \(h\) ist, dass ihre Auswertung billig ist. Die Auswertung sollte in konstant vielen Schritten vonstatten gehen. Nur wenn Sie billig ist, lohnt sich der Umweg über eine Hashfunktion.

24.3.3. Die Build-in Hashfunktion#

Bevor wir unsere eigene verbesserte Hashfunktion schreiben, nutzten wir doch einmal was uns Python bereits bietet.

Exercise 24.22 (Pythons Hashfunktion)

Lesen Sie die Dokumentation zur Python-Funktion hash. Sie finden diese hier.
Verwenden Sie hash als Ihre Hashfunktion. Bauen Sie dafür die Funktionen aus der vorherigen Aufgabe so um, dass sie diesen eine Hashfunktion hash_func als Argument übergeben können.
Führen Sie anschließend
```
hashtable = new_hash_table(unique_names_lex, hash_func=hash)
```
aus und beobachten Sie wie lange die Funktion arbeitet.

def index_of(name):
    return ord('A')-ord(name[0])

def search_index(name, hashtable, hash_func=hash):
    key = name
    index = hash_func(key) % len(hashtable)
    for i in range(len(hashtable)):
        j = (index+i) % len(hashtable)
        if hashtable[j] == key:
            return j
        if hashtable[j] == None:
            return j
        
    # there is no free place left
    return len(hashtable)

def contains(name, hashtable, hash_func=hash):
    index = search_index(name, hashtable, hash_func)
    return index < len(hashtable) and hashtable[index] == name

def get_value(name, hashtable, hash_func=hash):
    index = search_index(name, hashtable, hash_func)
    if index < len(hashtable) and hashtable[index] == name:
        return hashtable[index]
    else:
        None

def insert(name, hashtable, hash_func=hash):
    index = search_index(name, hashtable, hash_func)
    while index >= len(hashtable):
        hashtable.append(None)
        
    if hashtable[index] == name:
        return False
    else:
        hashtable[index] = name
        return True

def delete(name, hashtable, hash_func=hash):
    index = search_index(name, hashtable, hash_func)
    if index < len(hashtable) and hashtable[index] == name:
        hashtable[index] = None
        i = 1
        while(hashtable[index+i] != None):
            value = hashtable[index+i]
            hashtable[index+i] = None
            insert(value, hashtable, hash_func)
            i += 1
        return True
    else:
        return False

def new_hash_table(names, hash_func=hash):
    hashtable = [None for i in range(2*len(names) + 8)]
    for name in names:
        insert(name, hashtable, hash_func)
    return hashtable

Die Berechnungszeit ist deutlich kürzer. Lassen Sie uns erneut testen ob alles mit rechten Dingen zugeht.

hashtable = new_hash_table(unique_names_lex, hash_func=hash)
all([search_index(name, hashtable, hash_func=hash) == index 
     for index, name in enumerate(hashtable) 
     if name != None])

True

Exercise 24.23 (Kollisionen zählen)

Schreiben Sie eine Python-Funktion collisions(hashtable, hash_func), welche Ihnen für die Listenelemente der Liste hashtable die Kollisionen, abhängig von der Hashfunktion hash_func zählt. In anderen Worten collisions(hashtable, hash_func) berechnet die Anzahl die Kollisionen die stattgefunden haben um die Elemente in hashtable einzufügen.

Vergleiche Sie die Hashfunktionen index_of und hash.

def collisions(hashtable, hash_func=hash):
    collisions = 0
    for index, key in enumerate(hashtable):
        if key != None:
            j = hash_func(key) % len(hashtable)
            collisions += abs(j-index)
    return collisions

print(f'number of elements: {len(unique_names_lex)}')
print(f' collisions with hash: {collisions(new_hash_table(unique_names_lex, hash), hash)}')         # 16914
print(f' collisions with index_of: {collisions(new_hash_table(unique_names_lex, index_of), index_of)}') # 60751108

number of elements: 6782
 collisions with hash: 3505

 collisions with index_of: 60751108

16914 Kollisionen für das Einfügen von 6782 ist ein akzeptabler Schnitt. Das ist ca. 2.5 Kollision pro Element! index_of verursacht hingegen über 60 Millionen Kollisionen!

Im Abschnitt Python hatten wir erwähnt, dass Python aufwendige Berechnungen in C/C++-Coder verlagert. Dies ist auch für die Funktion hash der Fall. Im folgenden zeigen wir ihnen den Code der Hashfunktion hash für Zeichenketten. Bitte erschrecken Sie nicht. Sie brauchen den Code nicht verstehen! Die Berechnung von Hashwerten sieht oft nach viel Voodoo aus. Hier werden Zahlen mit sogenannten Bit-Verschiebungen manipuliert. Man sieht dem Code an, dass er auf Performance und nicht auf Lesbarkeit getrimmt ist.

static long
string_hash(PyStringObject *a)
{
    register Py_ssize_t len;
    register unsigned char *p;
    register long x;

#ifdef Py_DEBUG
    assert(_Py_HashSecret_Initialized);
#endif
    if (a->ob_shash != -1)
        return a->ob_shash;
    len = Py_SIZE(a);
    /*
      We make the hash of the empty string be 0, rather than using
      (prefix ^ suffix), since this slightly obfuscates the hash secret
    */
    if (len == 0) {
        a->ob_shash = 0;
        return 0;
    }
    p = (unsigned char *) a->ob_sval;
    x = _Py_HashSecret.prefix;
    x ^= *p << 7;
    while (--len >= 0)
        x = (1000003*x) ^ *p++;
    x ^= Py_SIZE(a);
    x ^= _Py_HashSecret.suffix;
    if (x == -1)
        x = -2;
    a->ob_shash = x;
    return x;
}

24.3.4. Eine eigene gute Hashfunktion#

Lassen Sie uns nun unsere eigene verbesserte Hashfunktion entwickeln. Wir suchen nach einer Funktion, welche verschiedene Zeichenketten in verschiedene natürliche Zahlen umwandelt. Verwenden wir nur ein Zeichen für die Berechnung ist klar, dass wir nicht mehr als 26 verschiedene Zahlen erwarten können.

Lassen Sie uns deshalb mehrere Zeichen für die Berechnung des Hashwerts verwenden. Eine erste Idee wäre die Summe der codierten Zeichen:

def hash_func_sum(name):
    hash_value = 0
    for char in name:
        hash_value += ord(char)
    return hash_value

print(collisions(new_hash_table(unique_names_lex, hash_func_sum), hash_func_sum))

20629463

Immerhin erreichen wir damit nur noch 20 Millionen Kollisionen, was jedoch immernoch viel zu viel ist. Wie sieht es mit der Multiplikation aus?

def hash_func_mul(name):
    hash_value = 0
    for char in name:
        hash_value *= ord(char)
    return hash_value

print(collisions(new_hash_table(unique_names_lex, hash_func_mul), hash_func_mul))

22994371

Etwas schlechter fällt hierfür das Ergebnis aus.

Exercise 24.24 (Hashfunktion der Addition und Multiplikation)

Warum sind die beiden Hashfunktion hash_func_sum und hash_func_mul, keine besonders guten Hashfunktionen?

Solution to Exercise 24.24 (Hashfunktion der Addition und Multiplikation)

Sowohl die Addition als auch die Multiplikation ist kommutativ. Deswegen fließt die Reihenfolge der Zeichen nicht in die Berechnung ein. Thomas und hasToh haben den gleichen Hashwert.

Erinnern wir uns zurück an die Darstellung von Zahlen im Binär- und Dezimalsystem, siehe Zahlen im Binärsystem. Auch hier haben wir aus einer Folge von Zeichen 0 und 1 eine eindeutige Zahl berechnet. Aus einer Zahl \(b_{n-1} \ldots b_2b_1b_0\) in Binärdarstellung haben wir die eindeutige Dezimalzahl

\[ \sum\limits_{i=0}^n b_i \cdot 2^{i} = b_0 \cdot 2^0 + b_1 \cdot 2^1 + \cdots b_{n-1} \cdot 2^{n-1} \]

berechnet. Dieses Berechnungsmuster können wir wiederverwenden!

Angenommen unsere Zeichenkette, interpretiert als Folge von Zahlen (ASCII), ist \(s_{n-1} \ldots s_2s_1s_0\) und \(p\) ist irgendeine Basis, dann ist

\[ \sum\limits_{i=0}^n s_i \cdot p^{i} = s_0 \cdot p^0 + s_1 \cdot p^1 + \cdots s_{n-1} \cdot p^{n-1} \]

eine eindeutige Dezimalzahl sofern \(p\) eine valide Basis ist.

Wie im Binärsystem als auch im Dezimalsystem muss \(p\) größer sein als alle Ziffern des Zahlensystems. In unserem Fall müsste \(p\) größer sein als ord("z"). Da wir jedoch keine unbedingte Eindeutigkeit benötigen ist ein kleineres \(p\) auch gültig.

Unsere Hashfunktion ist durch

(24.7)#\[h(s_{n-1} \ldots s_2s_1s_0) = \sum\limits_{i=0}^n s_i \cdot p^{i} = s_0 \cdot p^0 + s_1 \cdot p^1 + \cdots s_{n-1} \cdot p^{n-1}\]

gegeben.

Exercise 24.25 (Eindeutigkeit)

Was für ein kleines \(p\) könnte sich besonders gut eignen und warum?

Solution to Exercise 24.25 (Eindeutigkeit)

Eine Primzahl \(p\) eignet sich besonders gut, da dann die Produkte

\[ s_i \cdot p^{i} \text{ und } s_j \cdot p^{j} \text{ mit } i \neq j \]

nur gleich sein können, wenn \(p\) in der Faktorisierung von \(s_i\) oder \(s_j\) vorkommt. Ist \(p\) keine Primzahl gibt es mehr Möglichkeiten für die Gleichheit der beiden Produkte.

Sie sehen, wir tauchen ein wenig in die Zahlentheorie ein. Dieses mathematische Denken ist auch ein Teil des Computational Thinkings.

Exercise 24.26 (Eine gute Hashfunktion)

Implementieren Sie die Hashfunktion welche durch Gleichung (24.7) definiert ist. 83 eignet sich als Primzahl (nicht zu klein und groß genug).
Testen Sie Ihre neue Hashfunktion durch collisions.

def hash_func(name):
    hash_value = 0
    prime = 83
    for char in name:
        hash_value *= prime
        hash_value += ord(char)
    return hash_value

print(collisions(new_hash_table(unique_names_lex, hash_func), hash_func)) # 3432

Wir haben es geschafft!!! Nur noch 3432 Kollisionen! Damit sind wir für unseren Fall besser als die Python-Funktion hash.

Allerdings hängt die Berechnungszeit noch von der Anzahl der Zeichen eines Namen name ab. Wir könnten uns darauf einigen nur die ersten \(m\) Zeichen zu berücksichtige.

def hash_func(name):
    hash_value = 0
    prime = 83
    m = 8
    for i in range(min(m, len(name))):
        hash_value *= prime
        hash_value += ord(name[i])
    return hash_value
print(collisions(new_hash_table(unique_names_lex, hash_func), hash_func))

Das Ergebnis ist mit 3692 Kollisionen immernoch sehr gut und die Auswertung benötigt nun eine konstante Anzahl von maximal 8 Schritten.

24.3.5. Unser Dictionary#

Bislang können wir in unsere Hashtable Namen einfügen, löschen und abfragen ob sich ein Element in unserer Hashmap befindet:

insert('Dieter', hashtable, hash_func)
contains('Dieter', hashtable, hash_func)
delete('Dieter', hashtable, hash_func)

True

Die Funktionalität eines Dictionary haben wir damit noch nicht erreicht. Das besondere des Dictionary ist, dass es einen Schlüssel key und einen Wert value gibt und dass wir den Wert mit dem Schlüssel identifizieren können:

dictionary = {'Dieter': '1977-05-06', 'Bella': '1999-10-11'}
print(dictionary['Dieter'])
print(dictionary['Bella'])

1977-05-06
1999-10-11

Das ist genau dann sehr nützlich, wenn wir den Schlüssel einfach berechnen und auch hashen können, den Wert jedoch nicht. In unserer Hashtable sind Namen die Schlüssel, was bisher fehlt ist der Wert. Um unsere Hashtable um Werte zu erweitern, machen wir aus der Liste hashtable zwei gleich Lange Listen keys und values. Dafür müssen wir selbstverständlich alle bisher implementierten Funktionen anpassen.

Exercise 24.27 (Unser Dictionary)

Machen Sie aus der hashtable zwei Listen keys und values, sodass sich in keys die Schlüssel unseres Dictionary befinden und in values die Werte. Passen Sie alle Funktionen entsprechend an. Sie müssen folgenden Funktionen anpassen:

search_index
contains
get_value: Dies Funktion sollte nicht mehr den Schlüssel sondern den Wert zurückliefern!
insert: Sollte nur einen neuen Wert einfügen, falls es den entsprechenden Schlüssel noch nicht gibt.
delete
new_hash_table
collisions

Führen Sie zusätzlich eine Funktion set_value ein. Diese soll den Wert eines passend zum übergebenen Schlüssel ändert, sofern dieser existiert.

def search_index(key, hashtable, hash_func=hash):
    keys, values = hashtable
    index = hash_func(key) % len(keys)
    for i in range(len(keys)):
        j = (index+i) % len(keys)
        if keys[j] == key:
            return j
        if keys[j] == None:
            return j
        
    # there is no free place left
    return len(keys)

def contains(key, hashtable, hash_func=hash):
    keys, values = hashtable
    index = search_index(key, hashtable, hash_func)
    return index < len(keys) and keys[index] == key

def get_value(key, hashtable, hash_func):
    keys, values = hashtable
    index = search_index(key, hashtable, hash_func)
    if index < len(keys) and keys[index] == key:
        return values[index]
    else:
        None

def set_value(key, value, hashtable, hash_func):
    keys, values = hashtable
    index = search_index(key, hashtable, hash_func)
    if index >= len(keys):
        return False
    
    keys[index] = key
    values[index] = value
    return True

def insert(key, value, hashtable, hash_func=hash):
    keys, values = hashtable
    index = search_index(key, hashtable, hash_func)
    while index >= len(keys):
        keys.append(None)
        values.append(None)
      
    if keys[index] == key:
        return False
    else:
        keys[index] = key
        values[index] = value
        
        return True

def delete(key, hashtable, hash_func=hash):
    keys, values = hashtable
    index = search_index(key, hashtable, hash_func)
    if index < len(keys) and keys[index] == key:
        keys[index] = None
        values[index] = None
        i = 1
        while(keys[index+i] != None):
            next_key = keys[index+i]
            next_value = values[index+i]
            keys[index+i] = None
            values[index+i] = None
            insert(next_key, next_value, hashtable, hash_func)
            i += 1
        return True
    else:
        return False

def new_hash_table(keys, values, hash_func=hash):
    if len(keys) == len(values):
        hash_keys = [None for i in range(2*len(keys) + 8)]
        hash_values = [None for i in range(2*len(values) + 8)]
        hashtable = (hash_keys, hash_values)
        for key, value in zip(keys, values):
            insert(key, value, hashtable, hash_func)
        return hashtable
    return ([],[])

def collisions(hashtable, hash_func=hash):
    keys, values = hashtable
    collisions = 0
    for index, key in enumerate(keys):
        if key != None:
            j = hash_func(key) % len(keys)
            collisions += abs(j-index)
    return collisions

Tests:

keys = ['0', '1', '2']
values = ['Berta', 'Hans', 'Thomas']
hashtable = new_hash_table(keys, values, hash_func)
print(get_value('1', hashtable, hash_func))         # Hans
set_value('1', 'Peter', hashtable, hash_func)
print(get_value('1', hashtable, hash_func))         # Peter
print(insert('2', 'Anna', hashtable, hash_func))    # False
print(get_value('2', hashtable, hash_func))         # Thomas
print(insert('3', 'Anna', hashtable, hash_func))    # True
print(get_value('3', hashtable, hash_func))         # Anna

Hans
Peter
False
Thomas
True
Anna

Zusammen mit unseren Funktionen bildet das Paar keys, values unser eigenes Dictionary.

24.3.6. Hashtable Klasse (optional)#

Um die Funktionalität besser zu kapseln, können wir die Funktionalität mit samt der zwei Listen in eine Klasse Hashtable packen. Wir haben Ihnen diese zusammengestellt. new_hash_table haben wir durch insert_all ersetzt.

Zudem gibt es noch drei weitere Funktionen size, __has_to_resize und __resize. size liefert die Anzahl der Elemente in der Hashtable zurück. __has_to_resize ist genau dann wahr, wenn die Hashtable vergrößert oder verkleinert werden muss und __resize führt diese Anpassung durch.

Wann immer ein Element aus der Hashtable gelöscht oder eingefügt wird, testen wir mit __has_to_resize ob wir die Hashtable anpassen müssen. Ist die Hahstable \(2/3\) voll, dann wird sie vergrößert und ist sie nur \(1/6\) befüllt, wird sie verkleinert. Wann immer die Größe der Hahstable angepasst wird, wird diese auf \(1/4\) befüllt gesetzt. Alle Elemente werden neu eingefügt.

Exercise 24.28 (Größe der Hashtable)

Weshalb sollte die Hashtable nicht zu groß und nicht zu klein sein?

Solution to Exercise 24.28 (Größe der Hashtable)

Ist die Hashtable zu groß verbrauchen wir unnötig viel Speicher. Ist sie hingegen zu klein gibt es mehr und mehr Kollisionen und die Laufzeit der Funktionen der Hashtable erhöht sich!

class Hashtable():
    def __init__(self, hashf=None):
        if hashf == None:
            self.hash_func = self.hashf
        else:
            self.hash_func = hashf
        self.n = 0
        self.min_size = 8
        self.keys = [None for _ in range(self.min_size)]
        self.values = [None for _ in range(self.min_size)]

    def __search_index(self, key):
        index = self.hash_func(key) % len(self.keys)
        for i in range(len(self.keys)):
            j = (index+i) % len(self.keys)
            if self.keys[j] == key:
                return j
            if self.keys[j] == None:
                return j

        # there is no free place left
        return len(self.keys)

    def contains(self, key):
        index = self.__search_index(key)
        return index < len(self.keys) and self.keys[index] == key

    def get_value(self, key):
        index = self.__search_index(key)
        if index < len(self.keys) and self.keys[index] == key:
            return self.values[index]
        else:
            None

    def set_value(self, key, value):
        index = self.__search_index(key)
        if index >= len(self.keys):
            return False

        self.keys[index] = key
        self.values[index] = value
        return True

    def insert(self, key, value):
        index = self.__search_index(key)
        while index >= len(self.keys):
            self.keys.append(None)
            self.values.append(None)

        if self.keys[index] == key:
            return False
        else:
            self.keys[index] = key
            self.values[index] = value
            self.n += 1
            if(self.__has_to_resize()):
                self.__resize()
            return True

    def size(self):
        return self.n

    def __has_to_resize(self):
        if self.n <= self.min_size:
            return False
        else:
            return self.n > 4 / 6 * len(self.keys) or self.n < 1 / 6 * len(self.keys)

    def __resize(self):
        m = self.n * 4  # 1 / 4 filled
        old_keys = self.keys
        old_values = self.values
        self.keys = [None for _ in range(m)]
        self.values = [None for _ in range(m)]
        for key, value in zip(old_keys, old_values):
            if key != None:
                self.insert(key, value)

    def delete(self, key):
        index = self.__search_index(key)
        if index < len(self.keys) and self.keys[index] == key:
            self.keys[index] = None
            self.values[index] = None
            i = 1
            while(self.keys[index+i] != None):
                next_key = self.keys[index+i]
                next_value = self.values[index+i]
                self.keys[index+i] = None
                self.values[index+i] = None
                self.insert(next_key, next_value)
                i += 1
                if(self.__has_to_resize()):
                    self.__resize()
            return True
        else:
            return False

    def insert_all(self, keys, values):
        if len(keys) == len(values):
            hash_keys = [None for i in range(2*len(keys) + 8)]
            hash_values = [None for i in range(2*len(values) + 8)]
            hashtable = (hash_keys, hash_values)
            for key, value in zip(keys, values):
                self.insert(key, value)
            return hashtable
        return ([], [])

    def collisions(self):
        collisions = 0
        for index, key in enumerate(self.keys):
            if key != None:
                j = self.hash_func(key) % len(self.keys)
                collisions += abs(j-index)
        return collisions

    def hashf(self, name):
        hash_value = 0
        prime = 83
        m = 8
        for i in range(min(m, len(name))):
            hash_value *= prime
            hash_value += ord(name[i])
        return hash_value

Folgender Code zeigt die Verwendung der neuen Klasse

import hashtable
def simple_test():
    keys = ['0', '1', '2']
    values = ['Berta', 'Hans', 'Thomas']

    mydict = hashtable.Hashtable()
    mydict.insert_all(keys, values)

    print(mydict.get_value('1'))
    mydict.set_value('1', 'Peter')
    print(mydict.get_value('1'))
    print(mydict.insert('2', 'Anna'))
    print(mydict.get_value('2'))
    print(mydict.insert('3', 'Anna'))
    print(mydict.get_value('3'))


def insert_and_delete_test():
    n = 1000
    # intentionally bad hash function!
    mydict = hashtable.Hashtable(lambda i: int(i) % 100)
    for i in range(n):
        mydict.insert(str(i), i)

    for i in range(0, n, 10):
        mydict.delete(str(i))

    print(all([mydict.get_value(str(i)) ==
          i for i in range(n) if i % 10 != 0]))

simple_test()
insert_and_delete_test()

Hans
Peter
False
Thomas
True
Anna

True