20. Roboterwelt

Für diese Übung benötigen wir das Paket roboworld. Dieses können Sie sich durch

pip install roboworld

herunterladen und installieren.

Lernziel

Im ersten Teil dieser Übung machen wir Sie mit den Kontrollstrukturen von imperativen Programmiersprachen vertraut. Dazu tauchen Sie in eine vorgegebene Welt ein und lernen das WAS von dem WIE zu trennen (siehe Das Was und das Wie).

Im zweiten Teil werden wir interessante aber auch schwierigere Fragen diskutieren und durch Computational Thinking lösen und unser Denken dadurch trainieren.

In dieser Übung beschäftigen wir uns mit der Zufallsfahrt, determinierten und nicht-determinierten Algorithmen, Simulationen, Mittel- und Erwartungswert, Bäumen und der Tiefen- wie auch Breitensuche.

Roboter dienen uns heute in vielen Bereichen als Helfer und Assistenten. Sie fertigen Autos und andere große Maschinen an, spielen gegeneinander Fußball und interagieren mit uns Menschen auf direktem Weg. Roboter können dort eingesetzt werden, wo es für den Menschen zu gefährlich wird. Zum Beispiel, hatte man versucht durch einen Roboter die Lage am Kernreaktor von Chernobyl besser zu analysieren. Ein weiteres Beispiel ist die Entschärfung von Sprengstoff oder das Auffinden von Überlebenden welche unter Gebäuden begraben wurden.

Roboter agieren zu Land, Wasser als auch Luft – ob als Drohnen, kleine Schiffswrackentdecker oder Landschaftserkunder. Auch in unserem Alltag nehmen uns Roboter zunehmens die Arbeit ab. Ein prominentes Beispiel ist der Roboterstaubsauger, welcher autonom die Wohnung reinigt.

Das große Feld der künstlichen Intelligenz als auch der Robotik sind interdisziplinäre Gebiete die eng miteinander verwoben sind, denn ein Roboter ist im Grunde eine mechanische Konstruktion versehen mit einer künstlichen Intelligenz. Um eine solche künstliche Intelligenz soll es in diesem Kapitel gehen. Genauer gesagt beschäftigen wir uns mit der Frage, wie ein Roboter durch eine ihm unbekannte Welt navigieren kann.

20.1. Die Welt

Unser Roboter bewegt sich in einer vereinfachten Version unserer Welt. Zunächst einmal gibt es anstatt drei, lediglich zwei Dimensionen. Wir lassen die Höhe der Objekte weg. Man könnte auch sagen, dass wir uns im sogenannten Flachland befinden. Zusätzlich diskretisieren wir den Raum gleichmäßig in \(x\)- und \(y\)-Richtung, sodass unser Gebiet \(\Omega\) ein zweidimensionales diskretes gleichmäßiges Gitter ist. Das Gebiet ist außerdem beschränkt. Mathematisch können wir das Gebiet wie folgt definieren:

\[ \Omega \subset \mathbb{N} \times \mathbb{N}, \text{ und } |\Omega| = k \text{ für irgendein } k \in \mathbb{N}. \]

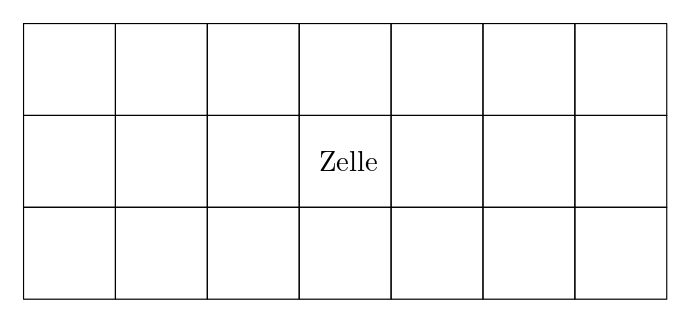
Abb. 20.1 Das diskrete Gebiet aus Zellen mit 3 Zeilen und 7 Spalten.

Einen Gitterpunkt nennen wir Zelle. Unser Roboter befindet sich in genau einer Zelle und kann von Zelle zu Zelle wandern, sofern die Zelle nicht durch ein anderes unpassierbares Objekt belegt ist. Eine Zelle hat einen von folgenden Zuständen:

Zusand	Farbe	Eigenschaft	Auswirkung
Leer	Hellgrau	pasierbar	Zelle ist derzeit pasierbar
Hindernis	Dunkelgrau	unverrückbares, unpassierbares Objekt	Zelle ist für immer unpassierbaf
Stein	Orange	verrückbares, unpassierbares Objekt	Zelle ist derzeit unpassierbar
Blatt	Grün	verrückbares, passierbares Objekt	Zelle ist derzeit pasierbar

Sowohl der Roboter robo als auch sein Ziel können sich auf einer Zelle befinden. Der Zustand der Zelle ändert sich dadurch nicht.

Um die Welt und Ihren Roboter anzuzeigen benötigen Sie das Paket roboworld.

import roboworld as rw

Es gibt verschiedene Methoden um verschiedene Welten zu erzeugen. Mit

world = rw.new_world(nrows = 5, ncols = 9)

erzeugen Sie ein Gebiet mit 5 Zeilen und 9 Spalten. Die Zelle in der linken unteren Ecke hat stets die Koordinate (0,0) und die obere rechte Zelle die Koordinate (nrows-1, ncols-1). Der Roboter wird bei dieser Form der Erzeugung in die Mitte des Gebiets gesetzt und das Ziel wird zufällig in eine Zelle gelegt.

Um sich die erzeugte Welt anzeigen zu lassen rufen Sie

world.show()

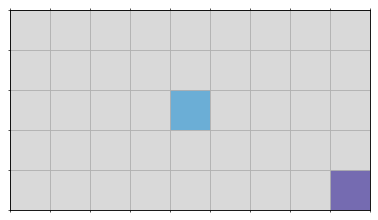
auf. Jede Zelle hat eine bestimmte Farbe, die ihren aktuellen Zustand beschreibt. Die Zelle auf der der Robeter steht ist blau und die Zelle des Ziels ist lila eingefärbt.

Die Welt ist eine statische Welt, welche nur vom Roboter selbst verändert werden kann. In anderen Worten, der Zustand einer Zellen bleibt solange unverändert bis Ihr Roboter diesen oder seinen eigenen Zustand verändert.

20.2. Der Roboter

Der Roboter kann sich durch ein Gebiet bewegen und verrückbare Objekte aufnehmen, herumtragen und wieder absetzten. Außerdem kann er eine Zelle, auf der er sich gerade befinden, mit set_mark() markieren oder eine Markierung von der aktuellen Zelle entfernen unset_mark(). Um dem Roboter Befehle zu erteilen müssen Sie ihn zunächst von der Welt durch

robo = world.robo

heranholen. Der Roboter hat eine Ausrichtung, d.h. seine Nase zeigt in eine von vier Himmelsrichtungen:

1. Norden 'N'

2. Osten 'E' (engl. east)

3. Süden 'S'

4. Westen 'W'

Der Roboter kann nur geradeaus laufen move() und sich nur nach links drehen turn_left(). Sie können durch is_facing_north() den Roboter fragen, ob er nach Norden ausgerichtet ist. Steht der Roboter an der Stelle (i,j) kann er durch mehrmaliges Drehen und einmal move() demnach nur die Zellen

1. (i+1,j),

2. (i-1,j),

3. (i,j+1) und

4. (i,j-1)

erreichen. Diese Nachbarschaft heißt im übrigen Von-Neumann-Nachbarschaft, siehe Abbildung 20.2. Beachten Sie, dass wir die Zeile zuerst nennen und von null beginnen zu zählen. (3,1) steht demnach für die Zeile 3 und Spalte 1 bzw. für die 4-te Zeile und 2-te Spalte.

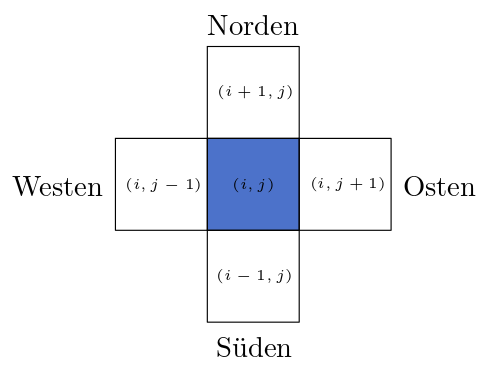
Abb. 20.2 Die Von-Neumann-Nachbarschaftsbeziehung.

Der Roboter kann durch is_wall_in_front() feststellen, ob direkt vor ihm ein Hindernis (oder der Rand des Gebiets) ist und durch is_mark_in_front() abfragen ob die Zelle vor ihm markiert ist.

Durch is_stone_in_front() können Sie den Roboter fragen, ob sich direkt vor ihm ein (verrückbarer) Stein befindet. Mit take_stone_in_front() können Sie diesen Stein aufnehmen und ihn mit put_stone_in_front() direkt vor dem Roboter absetzten (falls dies möglich ist). Dabei kann der Roboter jedoch nur einen Stein gleichzeitig tragen.

Im folgenden sehen Sie eine komplette Liste aller Methoden. Bitte nicht erschrecken, wir werden nicht alle benötigen und wir werden die notwendigen Methoden wiederholen. Sie können sich die Beschreibung auch durch help(robo) ansehen.

Methode	Beschreibung
is_facing_north()	Ist genau dann True, wenn der Roboter nach norden (oben) ausgerichtet ist
is_wall_in_front()	Ist genau dann True, wenn vor dem Roboter ein (unverrückbares) Hindernis ist
is_stone_in_front()	Ist genau dann True, wenn vor dem Roboter ein (verrückbarer) Stein ist
is_carrying_stone()	Ist genau dann True, wenn der Roboter einen Stein trägt
is_leaf_in_front()	Ist genau dann True, wenn sich vor dem Roboter Blatt befindet
is_carrying_leafs()	Ist genau dann True, wenn der Roboter mindestens ein Blatt trägt
is_at_goal()	Ist genau dann True, sich der Roboter an seinem Ziel befindet
toss()	Gibt mit gleicher Wahrscheinlichkeit entweder True oder False zurück
move()	Bewegung um eine Zelle nach vorne
turn_left()	Drehung um 90 Grad nach links
take_stone_in_front()	Nimmt einen Stein, der vor dem Roboter liegt, auf
put_stone_in_front()	Legt Stein vor den Roboter ab
take_leaf()	Nimmt einen Blatt auf, welches sich direkt unter dem Roboter befindet
put_leaf()	Legt (getragenes) direkt unter den Roboter ab Blatt ab
put_stone_in_front()	Legt (getragenen) Stein vor den Roboter ab
set_mark()	Markiert die Zelle auf der der Roboter steht
is_mark_in_front()	Ist genau dann True, wenn vor dem Roboter eine markierte Zelle ist
unset_mark()	Entfernt die Markierung von der Zelle auf der der Roboter steht

Sie rufen eine Methode method() durch

robo.method()

auf.

20.3. Einfache Erkundungen

Jede Welt besteht aus einer Aufgabe die Ihr Roboter lösen muss. Ob er erfolgreich war, können Sie mit

world.is_successful()

False

abfragen. Diese Methode der Welt gibt genau dann True zurück wenn die Aufgabe erfolgreich abgeschlossen ist.

20.3.1. Korridor

Unsere erste Welt die wir betrachten ist ein einfacher Korridor, welchen ihr Roboter von Westen nach Osten durchlaufen soll.

Führen Sie folgenden Code aus und lassen Sie sich damit die Welt ersteinmal anzeigen. Ihr Roboter befindet sich in der Zelle (0,0) und ist nach Osten ausgerichtet. Das Ziel befindet sich ganz im Osten.

world = rw.corridor()
robo = world.robo
world.show()

Exercise 20.1 (Mühsames Durchwandern des Korridors)

Laufen Sie mit Ihrem Roboter zum Ziel. Verwenden Sie dabei keine Schleifen.

Show code cell source Hide code cell source

robo.move()
robo.move()
robo.move()
robo.move()
robo.move()
robo.move()
robo.move()
robo.move()
robo.move()

world.is_successful()

move (0, 0) -> (0, 1)
move (0, 1) -> (0, 2)
move (0, 2) -> (0, 3)
move (0, 3) -> (0, 4)
move (0, 4) -> (0, 5)
move (0, 5) -> (0, 6)
move (0, 6) -> (0, 7)
move (0, 7) -> (0, 8)
move (0, 8) -> (0, 9)

True

Exercise 20.2 (Kollision)

Führen Sie den obigen Code (ohne die Erzeugung der Welt) mehrfach aus. Was beobachten Sie? Welche Ursache hat Ihre Beobachtung?

Solution to Exercise 20.2 (Kollision)

Nachdem der Roboter am Ziel angekommen ist und wir erneut mit ihm nach vorne ziehen, läuft er gegen die Gebietsgrenze. Das führt zu einem Fehler (einer WallInFrontException).

Sie können sich die Wanderung ihres Roboters auch ansehen. Rufen Sie dazu

rw.animate(world)

Once Loop Reflect

auf.

Animation

Das Animieren der Welt kann nur einmal am Ende Ihrer Wanderung ausgeführt werden, da der Speicher (die Wanderung) danach vergessen wird.

Exercise 20.3 (Festes Durchwandern des Korridors)

Lösen Sie das Problem erneut, verwenden Sie dabei das

for ... in range(...)

Konstrukt. Sie können eine frische neue Welt erzeugen.

Show code cell source Hide code cell source

world = rw.corridor()
robo = world.robo

for _ in range(9):
    robo.move()

print(world.is_successful())
world.show()

move (0, 0) -> (0, 1)
move (0, 1) -> (0, 2)
move (0, 2) -> (0, 3)
move (0, 3) -> (0, 4)
move (0, 4) -> (0, 5)
move (0, 5) -> (0, 6)
move (0, 6) -> (0, 7)
move (0, 7) -> (0, 8)
move (0, 8) -> (0, 9)
True

Sie können sich auch Korridore unterschiedlicher Länge konstruieren. Dazu rufen Sie

world = rw.corridor(length)

mit einem Argument length auf, wobei length eine positive Zahl größer gleich 2 sein muss. Zum Beispiel:

world = rw.corridor(20)
world.show()

Exercise 20.4 (Durchwandern des variablen Korridors)

Durchwandern Sie nun einen Korridor dessen Länge Sie nicht kennen. Welche Methode hilft Ihnen festzustellen ob Sie am Ende angekommen sind?

Show code cell source Hide code cell source

length = 25
world = rw.corridor(length)
robo = world.robo

while not robo.is_wall_in_front():
    robo.move()

print(world.is_successful())
world.show()

move (0, 0) -> (0, 1)
move (0, 1) -> (0, 2)
move (0, 2) -> (0, 3)
move (0, 3) -> (0, 4)
move (0, 4) -> (0, 5)
move (0, 5) -> (0, 6)
move (0, 6) -> (0, 7)
move (0, 7) -> (0, 8)
move (0, 8) -> (0, 9)
move (0, 9) -> (0, 10)
move (0, 10) -> (0, 11)
move (0, 11) -> (0, 12)
move (0, 12) -> (0, 13)
move (0, 13) -> (0, 14)
move (0, 14) -> (0, 15)
move (0, 15) -> (0, 16)
move (0, 16) -> (0, 17)
move (0, 17) -> (0, 18)
move (0, 18) -> (0, 19)
move (0, 19) -> (0, 20)
move (0, 20) -> (0, 21)
move (0, 21) -> (0, 22)
move (0, 22) -> (0, 23)
move (0, 23) -> (0, 24)
True

Bis jetzt bewegen wir unseren Roboter nur in eine Richtung. Was ist aber wenn wir nicht wissen wie der Roboter am Anfang ausgerichtet ist? Durch den Aufruf

length = 25
world = rw.corridor(length, random_headway=True)

wird ihr Roboter zufällig ausgerichtet.

Exercise 20.5 (Durchwandern des variablen Korridors mit variabler Ausrichtung)

Durchwandern Sie nun einen Korridor dessen Länge Sie nicht kennen, wobei Sie auch nicht wissen wie Ihr Roboter zu Beginn ausgerichtet ist. Testen Sie Ihren Code indem Sie ihn mehrfach ausführen.

Show code cell source Hide code cell source

length = 25
world = rw.corridor(length, random_headway=True)
robo = world.robo

# be sure that robo is facing north
while not robo.is_facing_north():
    robo.turn_left()
# we need three left turns to head east
robo.turn_left()
robo.turn_left()
robo.turn_left()
while not robo.is_wall_in_front():
    robo.move()

print(world.is_successful())
world.show()

turn W -> S
turn S -> E
turn E -> N
turn N -> W
turn W -> S
turn S -> E
move (0, 0) -> (0, 1)
move (0, 1) -> (0, 2)
move (0, 2) -> (0, 3)
move (0, 3) -> (0, 4)
move (0, 4) -> (0, 5)
move (0, 5) -> (0, 6)
move (0, 6) -> (0, 7)
move (0, 7) -> (0, 8)
move (0, 8) -> (0, 9)
move (0, 9) -> (0, 10)
move (0, 10) -> (0, 11)
move (0, 11) -> (0, 12)
move (0, 12) -> (0, 13)
move (0, 13) -> (0, 14)
move (0, 14) -> (0, 15)
move (0, 15) -> (0, 16)
move (0, 16) -> (0, 17)
move (0, 17) -> (0, 18)
move (0, 18) -> (0, 19)
move (0, 19) -> (0, 20)
move (0, 20) -> (0, 21)
move (0, 21) -> (0, 22)
move (0, 22) -> (0, 23)
move (0, 23) -> (0, 24)
True

Unser Roboter kann sich nur nach links drehen und wir können nur feststellen ob er gerade nach Norden ausgerichtet ist. Aus diesen beiden primitiven Operationen können wir jedoch kompliziertere Operationen durch Komposition erzeugen.

Um den Roboter nach Osten auszurichten, drehen wir ihn solange nach links bis er nach Norden ausgerichtet ist. Dann wissen wir, dass dreimal nach links drehen gleich einmal nach rechts drehen entspricht und wir somit den erwünschten Effekt erzielen.

Um diese neue Operation nach Osten ausrichten turn_east(robo) bequem in unserem Arsenal zu haben, extrahieren wir sie in eine eigene Funktion.

Exercise 20.6 (Nach Osten Ausrichten)

Implementieren Sie die Funktion turn_east(robo). Sie müssen lediglich Ihren bereits geschriebenen Code in die Funktion packen. Dabei ist das Argument robo ihr Roboter. Verwenden Sie daraufhin Ihre soeben geschriebene Funktion um die Aufgabe Exercise 20.5 zu lösen.

Show code cell source Hide code cell source

def turn_east(robo):
    # be sure that robo is facing north
    while not robo.is_facing_north():
        robo.turn_left()
        
    # we need three left turns to head west
    robo.turn_left()
    robo.turn_left()
    robo.turn_left()

length = 25
world = rw.corridor(length, random_headway=True)

robo = world.robo
turn_east(robo)
while not robo.is_wall_in_front():
    robo.move()

print(world.is_successful())
world.show()

turn E -> N
turn N -> W
turn W -> S
turn S -> E
move (0, 0) -> (0, 1)
move (0, 1) -> (0, 2)
move (0, 2) -> (0, 3)
move (0, 3) -> (0, 4)
move (0, 4) -> (0, 5)
move (0, 5) -> (0, 6)
move (0, 6) -> (0, 7)
move (0, 7) -> (0, 8)
move (0, 8) -> (0, 9)
move (0, 9) -> (0, 10)
move (0, 10) -> (0, 11)
move (0, 11) -> (0, 12)
move (0, 12) -> (0, 13)
move (0, 13) -> (0, 14)
move (0, 14) -> (0, 15)
move (0, 15) -> (0, 16)
move (0, 16) -> (0, 17)
move (0, 17) -> (0, 18)
move (0, 18) -> (0, 19)
move (0, 19) -> (0, 20)
move (0, 20) -> (0, 21)
move (0, 21) -> (0, 22)
move (0, 22) -> (0, 23)
move (0, 23) -> (0, 24)
True

Exercise 20.7 (Zur Wand laufen)

Extrahieren Sie nun den Code, der den Roboter zur Wand laufen lässt, in eine Funktion walk_to_wall(robo).

Show code cell source Hide code cell source

def walk_to_wall(robo):
    while not robo.is_wall_in_front():
        robo.move()

length = 25
world = rw.corridor(length, random_headway=True)
robo = world.robo

turn_east(robo)
walk_to_wall(robo)

print(world.is_successful())
world.show()

turn E -> N
turn N -> W
turn W -> S
turn S -> E
move (0, 0) -> (0, 1)
move (0, 1) -> (0, 2)
move (0, 2) -> (0, 3)
move (0, 3) -> (0, 4)
move (0, 4) -> (0, 5)
move (0, 5) -> (0, 6)
move (0, 6) -> (0, 7)
move (0, 7) -> (0, 8)
move (0, 8) -> (0, 9)
move (0, 9) -> (0, 10)
move (0, 10) -> (0, 11)
move (0, 11) -> (0, 12)
move (0, 12) -> (0, 13)
move (0, 13) -> (0, 14)
move (0, 14) -> (0, 15)
move (0, 15) -> (0, 16)
move (0, 16) -> (0, 17)
move (0, 17) -> (0, 18)
move (0, 18) -> (0, 19)
move (0, 19) -> (0, 20)
move (0, 20) -> (0, 21)
move (0, 21) -> (0, 22)
move (0, 22) -> (0, 23)
move (0, 23) -> (0, 24)
True

20.3.2. Einschub: Benennung

Loht es sich wirklich diese zwei Codezeilen in eine eigene Funktion zu packen? Zwei Gründe offenbaren sich hier:

1. Lesbarkeit und

2. Wiederverwendbarkeit.

20.3.2.1. Lesbarkeit

Selbst wenn die Zeilen

while not robo.is_wall_in_front():
    robo.move()

einfach zu verstehen sind, so müssen wir dennoch Zeit investieren um die while-Schleife und die zwei Methoden zu lesen und in Kombination zu verstehen. Befinden sich diese Codezeilen in einer langen Codesequenz wird es nicht leichter.

Wir wollen mit diesen beiden Zeilen gerade bewirken, dass der Roboter zur nächsten Wand vor ihm läuft. Unser Gehirn hat diese Aufgabe bereits gelöst, weshalb sollten wir also Denkressourcen vergeuden, wenn wir nach einer gewissen Zeit wieder zu diesem Code zurückkehren? Da wir vergessen, müssen wir erneut feststellen WAS diese beiden Zeilen bewirken. Wir könnten die Zeilen auch mit Kommentaren versehen:

# move to wall in front
while not robo.is_wall_in_front():
    robo.move()

Doch nichts dient der Dokumentation besser als wohlstrukturierter Code mit sprechenden und wohlüberlegten Variablen- und Funktionsnamen. Diese Benennung ist eine Kunst für sich. Wir haben uns für den Namen walk_to_wall entschieden.

In der Informatik ist die Sprache der Wahl Englisch, daran müssen Sie sich gewöhnen. Die Gemeinschaft ist international, zudem ist Englisch oft prägnanter und kürzer als Deutsch.

Andere Namen wären ebenso denkbar, z.B. würde walk_to_wall_in_front noch genauer beschreiben, WAS passiert. Doch zu lange Namen erschweren das Lesen, was den Vorteil der Strukturierung zunichte macht. Unserem Gehirn fällt es einfach sich an einen bestimmten Namen zu erinnern und sich über den Namen an den bereits betrachteten Code und dessen Auswirkung zu erinnern. Deshalb ist ein kurzer Name der viel über die Methode aussagt aber nicht alles im Detail beschreibt ein guter Name. Zum Beispiel wäre turn_left_move_one_cell_forward_turn_left() ein schlechter Name, obwohl er genau beschreibt was die Methode macht. Besser wäre, z.B., move_left_corner() oder take_left_turn().

Es ist ein Abwägen zwischen: Wie viel Wissen können wir bei der Leserschaft vorraussetzen und wie lange sollte der Name maximal werden. Das Wissen bezieht sich zum einen auf die Codebasis, also wie viel von unserem Code hat der Leser bereits verstanden, aber zum anderen auch auf das Anwendungsgebiet. Für Klimaforscher*innen ist vermutlich klar was

ocean.mean_temperature()

bedeuten könnte. Gute Namen berücksichtigen die Zielgruppe.

Namen sollten auch konsistent gewählt werden. Zum Beispiel haben wir uns entschieden alle Methoden des Roboters die entweder True oder False zurückgeben mit is zu beginnen. Es wäre inkonsistent wenn es eine Methode is_wall_in_front() und stone_in_front() gäbe. Inkonsistenz verlangt beim Lesen mehr mentale Anstrengung, was zu vermeiden ist. Es ist Verschwendung geistiger Kraft. Unser Gehirn ist eine visuelle Mustererkennungsmaschine, deshalb ist nicht nur der Name an sich wichtig sondern auch die visuelle Darstellung des Codes.

Um dieses Argument noch zu untermauern blicken wir auf folgendes bekanntes Beispiel. Sehen Sie sich folgendes Spielchen an: Sie haben die Menge \(M = \{a,b,c,d,e,f,g,h,i\}\) und acht Teilmengen \(\{a,b,c\}\), \(\{d,e,f\}\), \(\{g,h,i\}\), \(\{a,d,g\}\), \(\{b,e,h\}\), \(\{c,f,i\}\), \(\{a,e,i\}\) und \(\{c,e,g\}\). Sie spielen zu zweit und jeder wählt nacheinander ein Element aus \(M\). Jedes dieser Elemente kann nur einmal gewählt werden. Ziel ist es als erster Elemente zu wählen, sodass man alle Elemente einer der acht Teilmengen besitzt.

In dieser Art und Weise formuliert, fällt es unserem Gehirn sehr schwer das Spiel zu spielen. Dabei ist das Spiel nichts anderes als Tic-Tac-Toe. In visueller Form, ist das Spiel sehr einfach zu verstehen:

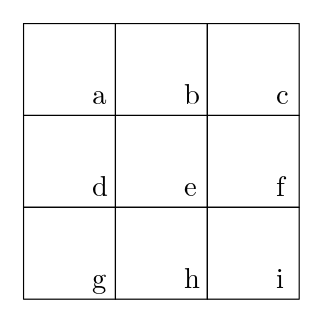
Gewisse Konsistenzen können wir nicht selbst wählen, da wir an einer Gemeinschaft teilnehmen. Zum Beispiel trennen wir in Python die Wörter, die einen Variablen- oder Funktions-/Methodennamen ausmachen durch den Unterstrick _ und zwar nicht weil es zwangsläufig die beste Art und Weise ist, sondern weil sich die Python-Gemeinschaft darauf geeinigt hat. In Java verwendet man hingegen die sogenannte Camel-Caps-Schreibweise: isWallInFront().

Solche Normen erleichtern die Zusammenarbeit ungemein. Es lohnt sich frühzeitig diese Normen nachzuschlagen oder den Code von anderen Programmierer*innen, auch wegen der Benennung von Variablen und Funktionen/Methoden, zu betrachten.

20.3.2.2. Wiederverwendbarkeit

Gute Programmierer*innen sind faul. Faul in dem Sinne, dass wir Maschinen für uns arbeiten lassen. Und faul in dem Sinne, dass wir keine Aufgabe zweimal lösen, egal wie klein die Aufgabe auch war!

Finden Sie in Ihrem Code an mehreren Stellen das gleiche Muster wird es Zeit dieses Muster zu abstrahieren und wiederzuverwenden. Das obige Beispiel verdeutlicht wie ‚klein/kurz‘ dieses Muster sein kann.

Selbst wenn Sie den Code noch nicht an mehreren Stellen verwenden, dieser aber eine bestimmte Aufgabe löst, sollten Sie darüber nachdenken diesen in eine eigene Funktion zu kapseln. Denken Sie an Ihr zukünftiges ich oder an andere Programmierer*innen, die auf ihrem Code aufbauen. Je kleiner die Aufgabe ist, die gekapselt werden kann, desto kleiner sind Ihre Schritte hin zur Lösung einer größeren Aufgabe und desto leichter wird es Ihnen fallen. Sie befreien sich von der kleinen Aufgabe, können diese abhaken und voranschreiten.

Das ist vergleichbar mit einer Einkaufsliste. Sie schreiben diese Liste nicht weil Sie zu doof oder zu faul sind, um sich zu merken was Sie einkaufen möchten. Nein! Sie schreiben diese Liste damit Sie sich der nächsten Aufgabe des Tages widmen können. Sie schreiben diese Liste damit Sie während des Einkaufens auf andere Dinge, wie zum Beispiel Ihre Umgebung, besser eingehen können. In anderen Worten, damit Sie mental für andere Aufgaben gewadmet sind, denn das Problem was Sie einkaufen möchten ist ja bereits gelöst.

Exercise 20.8 (Ein irrer Läufer)

Eraten Sie was folgender Code bewirken soll. Wo befindet sich der Roboter, wenn er ganz im Westen und nach Osten ausgerichtet startet?

for _ in range(5):
    walk_to_wall(robo)
    turn(robo) # turn zu deutsch 'umdrehen'

Implementieren Sie turn(robo) und führen Sie den Code aus. Lassen Sie sich die Animation anzeigen.

Solution to Exercise 20.8 (Ein irrer Läufer)

Der Roboter läuft zur Wand vor ihm und dreht sich um 180 Grad. Das wiederholt er fünfmal, somit läuft er hin und her. Am Ende befindet er sich ganz im Osten am Ziel.

Show code cell source Hide code cell source

length = 25
world = rw.corridor(length)
robo = world.robo

def turn(robo):
    robo.turn_left()
    robo.turn_left()

for _ in range(5):
    walk_to_wall(robo)
    turn(robo)

rw.animate(world)

move (0, 0) -> (0, 1)
move (0, 1) -> (0, 2)
move (0, 2) -> (0, 3)
move (0, 3) -> (0, 4)
move (0, 4) -> (0, 5)
move (0, 5) -> (0, 6)
move (0, 6) -> (0, 7)
move (0, 7) -> (0, 8)
move (0, 8) -> (0, 9)
move (0, 9) -> (0, 10)
move (0, 10) -> (0, 11)
move (0, 11) -> (0, 12)
move (0, 12) -> (0, 13)
move (0, 13) -> (0, 14)
move (0, 14) -> (0, 15)
move (0, 15) -> (0, 16)
move (0, 16) -> (0, 17)
move (0, 17) -> (0, 18)
move (0, 18) -> (0, 19)
move (0, 19) -> (0, 20)
move (0, 20) -> (0, 21)
move (0, 21) -> (0, 22)
move (0, 22) -> (0, 23)
move (0, 23) -> (0, 24)
turn E -> N
turn N -> W
move (0, 24) -> (0, 23)
move (0, 23) -> (0, 22)
move (0, 22) -> (0, 21)
move (0, 21) -> (0, 20)
move (0, 20) -> (0, 19)
move (0, 19) -> (0, 18)
move (0, 18) -> (0, 17)
move (0, 17) -> (0, 16)
move (0, 16) -> (0, 15)
move (0, 15) -> (0, 14)
move (0, 14) -> (0, 13)
move (0, 13) -> (0, 12)
move (0, 12) -> (0, 11)
move (0, 11) -> (0, 10)
move (0, 10) -> (0, 9)
move (0, 9) -> (0, 8)
move (0, 8) -> (0, 7)
move (0, 7) -> (0, 6)
move (0, 6) -> (0, 5)
move (0, 5) -> (0, 4)
move (0, 4) -> (0, 3)
move (0, 3) -> (0, 2)
move (0, 2) -> (0, 1)
move (0, 1) -> (0, 0)
turn W -> S
turn S -> E
move (0, 0) -> (0, 1)
move (0, 1) -> (0, 2)
move (0, 2) -> (0, 3)
move (0, 3) -> (0, 4)
move (0, 4) -> (0, 5)
move (0, 5) -> (0, 6)
move (0, 6) -> (0, 7)
move (0, 7) -> (0, 8)
move (0, 8) -> (0, 9)
move (0, 9) -> (0, 10)
move (0, 10) -> (0, 11)
move (0, 11) -> (0, 12)
move (0, 12) -> (0, 13)
move (0, 13) -> (0, 14)
move (0, 14) -> (0, 15)
move (0, 15) -> (0, 16)
move (0, 16) -> (0, 17)
move (0, 17) -> (0, 18)
move (0, 18) -> (0, 19)
move (0, 19) -> (0, 20)
move (0, 20) -> (0, 21)
move (0, 21) -> (0, 22)
move (0, 22) -> (0, 23)
move (0, 23) -> (0, 24)
turn E -> N
turn N -> W
move (0, 24) -> (0, 23)
move (0, 23) -> (0, 22)
move (0, 22) -> (0, 21)
move (0, 21) -> (0, 20)
move (0, 20) -> (0, 19)
move (0, 19) -> (0, 18)
move (0, 18) -> (0, 17)
move (0, 17) -> (0, 16)
move (0, 16) -> (0, 15)
move (0, 15) -> (0, 14)
move (0, 14) -> (0, 13)
move (0, 13) -> (0, 12)
move (0, 12) -> (0, 11)
move (0, 11) -> (0, 10)
move (0, 10) -> (0, 9)
move (0, 9) -> (0, 8)
move (0, 8) -> (0, 7)
move (0, 7) -> (0, 6)
move (0, 6) -> (0, 5)
move (0, 5) -> (0, 4)
move (0, 4) -> (0, 3)
move (0, 3) -> (0, 2)
move (0, 2) -> (0, 1)
move (0, 1) -> (0, 0)
turn W -> S
turn S -> E
move (0, 0) -> (0, 1)
move (0, 1) -> (0, 2)
move (0, 2) -> (0, 3)
move (0, 3) -> (0, 4)
move (0, 4) -> (0, 5)
move (0, 5) -> (0, 6)
move (0, 6) -> (0, 7)
move (0, 7) -> (0, 8)
move (0, 8) -> (0, 9)
move (0, 9) -> (0, 10)
move (0, 10) -> (0, 11)
move (0, 11) -> (0, 12)
move (0, 12) -> (0, 13)
move (0, 13) -> (0, 14)
move (0, 14) -> (0, 15)
move (0, 15) -> (0, 16)
move (0, 16) -> (0, 17)
move (0, 17) -> (0, 18)
move (0, 18) -> (0, 19)
move (0, 19) -> (0, 20)
move (0, 20) -> (0, 21)
move (0, 21) -> (0, 22)
move (0, 22) -> (0, 23)
move (0, 23) -> (0, 24)
turn E -> N
turn N -> W

Once Loop Reflect

Erinnern Sie sich an die obige Aufgabe Exercise 20.6. Dort haben wir eine Funktion turn_east(robo) implementiert. Weshalb erweitern wir unseren Werkzeugkasten nicht um turn_north(robo), turn_west(robo) und turn_south(robo).

Exercise 20.9 (Drehungen)

Implementieren Sie turn_north(robo), turn_west(robo) und turn_south(robo). Vermeiden Sie doppelten Code! Verwenden Sie turn(robo). Sie müssen unter Umständen turn_east(robo) anpassen.

turn_east(robo) verwendet bereits turn_north(robo), deshalb ergibt sich folgender Code:

Show code cell source Hide code cell source

def turn_north(robo):
    while not robo.is_facing_north():
        robo.turn_left()

def turn_west(robo):
    turn_north(robo)
    robo.turn_left()

def turn_south(robo):
    turn_north(robo)
    turn(robo)

def turn_east(robo):
    turn_west(robo)
    turn(robo)

20.3.3. Korridor mit Steinen

Die nächste Welt, die unser Roboter durchlaufen soll, ist ein Korridor der Steine auf dem Weg zum Ziel enthalten kann.

Der Roboter kann über diese nicht einfach drüber steigen. Er muss einen Stein der vor ihm liegt aufnehmen take_stone_in_front() und kann dann erst wieder weiterlaufen. Zudem kann der Roboter nur einen Stein gleichzeitig tragen. Falls er einen Stein trägt, kann er ihn mit put_stone_in_front() vor ihm ablegen. Sie können mit is_stone_in_front() prüfen ob vor dem Roboter ein Objekt liegt.

Mit

length = 25
nstones = 4
world = rw.corridor(length=length, nstones=nstones)
robo = world.robo
world.show()

erstellen Sie eine Welt mit einem Korridor der Länge 25 welcher 4 Objekte enthält. Diese Objekte werden zufällig in freien Zellen des Korridors verteilt.

Exercise 20.10 (Der Lauf nach Osten mit verrückbaren Hindernissen)

Lassen Sie Ihren Roboter erneut einmal von Westen nach Osten durch die Welt

world = rw.corridor(length=25, random_headway=True, nstones=4)

laufen. Implementieren Sie geeignete Funktionen um Ihren Code lesbar zu halten.

Um ein Objekt aus dem Weg zu räumen definieren wir die Funktion move_stone(robo). Diese lässt den Roboter das Objekt, welches sich vor ihm befindet, aufnehmen und hinter sich ablegen.

Show code cell source Hide code cell source

def move_stone(robo):
    robo.take_stone_in_front()
    turn(robo)
    robo.put_stone_in_front()
    turn(robo)

Eine weitere Funktion walk(robo) lässt den Roboter, solange nichts im Weg ist (nothing_in_front(robo)), laufen.

Show code cell source Hide code cell source

def nothing_in_front(robo):
    return not robo.is_wall_in_front() and not robo.is_stone_in_front()

def walk(robo):
    while nothing_in_front(robo):
        robo.move()

Schließlich können wir unseren Roboter loslaufen lassen:

Show code cell source Hide code cell source

turn_east(robo)
walk(robo)
while not robo.is_wall_in_front():
    move_stone(robo)
    walk(robo)

print(world.is_successful())

turn E -> N
turn N -> W
turn W -> S
turn S -> E
move (0, 0) -> (0, 1)
move (0, 1) -> (0, 2)
move (0, 2) -> (0, 3)
move (0, 3) -> (0, 4)
move (0, 4) -> (0, 5)
move (0, 5) -> (0, 6)
move (0, 6) -> (0, 7)
move (0, 7) -> (0, 8)
move (0, 8) -> (0, 9)
move (0, 9) -> (0, 10)
move (0, 10) -> (0, 11)
move (0, 11) -> (0, 12)
take stone at (0, 13)
turn E -> N
turn N -> W
put stone at (0, 11)
turn W -> S
turn S -> E
move (0, 12) -> (0, 13)
take stone at (0, 14)
turn E -> N
turn N -> W
put stone at (0, 12)
turn W -> S
turn S -> E
move (0, 13) -> (0, 14)
move (0, 14) -> (0, 15)
move (0, 15) -> (0, 16)
move (0, 16) -> (0, 17)
take stone at (0, 18)
turn E -> N
turn N -> W
put stone at (0, 16)
turn W -> S
turn S -> E
move (0, 17) -> (0, 18)
move (0, 18) -> (0, 19)
move (0, 19) -> (0, 20)
move (0, 20) -> (0, 21)
move (0, 21) -> (0, 22)
take stone at (0, 23)
turn E -> N
turn N -> W
put stone at (0, 21)
turn W -> S
turn S -> E
move (0, 22) -> (0, 23)
move (0, 23) -> (0, 24)
True

Exercise 20.11 (Eine unmögliche Aufgabe)

1. Funktioniert unser bzw. Ihr Code auch wenn keine Steine vorhanden sind?

2. Funktioniert unser bzw. Ihr Code für jeden möglichen Korridor mit Steinen?

3. Gibt es einen Korridor mit Steinen den wir unmöglich durchwandern können?

Solution to Exercise 20.11 (Eine unmögliche Aufgabe)

1. Ja, unser Code funktioniert auch wenn keine Steine vorhanden sind.

2. Nein, falls zu Beginn ein Stein direkt vor uns ist, können wir ihn nicht beiseite schaffen. Wir müssten ihn aufnehmen und mindestens einen Schritt noch vorne laufen um ihn dann ablegen zu können.

3. Ja, falls zu beginn direkt zwei oder mehr Steine vor uns liegen. Wir haben dann keine Möglichkeit diese beiseite zu schaffen.

Anstatt einen Stein aufzunehmen und ihn direkt wieder abzulegen, können wir ihn auch aufnehmen und erst dann ablegen wenn es notwendig ist.

Show code cell source Hide code cell source

def put_behind(robo):
    turn(robo)
    robo.put_stone_in_front()
    turn(robo)

turn_east(robo)
walk(robo)
while not robo.is_wall_in_front():
    robo.take_stone_in_front()
    walk(robo)
    put_behind(robo)

print(world.is_successful())

turn E -> N
turn N -> W
turn W -> S
turn S -> E
True

Dieser Code funktioniert auch wenn direkt am Anfang ein Stein auf uns wartet.

20.4. Komplexere Erkundungen

20.4.1. Zufallslauf

Die nächste Aufgabe besteht darin durch ein quadratisches Gebiet ohne Hindernisse mithilfe des Zufalls zu navigieren.

Betrachten wir ein quadratisches Gebiet mit nrow Zeilen und ncols Spalten (nrow == ncols) ohne Steine oder Hindernisse, wobei sich der Roboter im Zentrum und sein Ziel an einen zufälligen Ort befinden:

nrows = 5
ncols = 5
world = rw.new_world(nrows=nrows, ncols=ncols)
robo = world.robo
world.show()

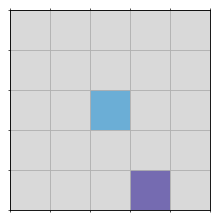
Eine, nicht besonders schlaue Strategie um zum Ziel zu laufen ist es zufällig eine der vier Nachbarn der Von-Neumann-Nachbarschaft als nächste Zelle auszuwählen. Diese Art der Fortbewegung nennt man Zufallslauf (engl. Random Walk).

Exercise 20.12 (Der Zufallslauf)

Implementieren Sie eine Funktion random_walk(robo), welche den Roboter robo solange den Zufallslauf ausführen lässt, bis er sein Ziel is_at_goal() erreicht hat.

Tipp: Eventuell nutzt Ihnen die Funktion choice() des Pakets random.

Show code cell source Hide code cell source

import random

def random_turn(robo):
    turns = random.choice([0,1,2,3])
    for _ in range(turns):
        robo.turn_left()

def random_walk(robo):
    required_steps = 0
    while not robo.is_at_goal():
        random_turn(robo)
        if not robo.is_wall_in_front():
            robo.move()
            required_steps = required_steps + 1
    return required_steps

robo.disable_print()
random_walk(robo)
print(world.is_successful())
rw.animate(world)

True

Once Loop Reflect

Ziemlich cool oder? Wir haben zwar einen sehr ineffektiven Algorithmus aber irgendwann findet er das Ziel des Roboters.

Möchten wir den Algorithmus analysieren ergeben sich interessante Fragen. Zum Beispiel, wie viele Schritte der Roboter im Durchschnitt machen muss oder anders gefragt:

Was ist der Erwartungswert für die Anzahl der Schritte, d.h. Aufrufe von move()?

Den umgangsprachlichen Durchschnitt von zwei oder mehreren Zahlen nennen wir in der Mathematik Mittelwert oder arithmetisches Mittel. Der Erwartungswert (manchmal leider auch als Mittelwert bezeichnet) ist eine Zahl, die angibt welchen Wert eine Zufallsvariable im Mittel annimmt. Diese zwei Dinge sind grundverschieden! Im Fall des Mittelwerts sprechen wir vom durchschnittlichen Wert konkreter Zahlen und im Fall des Erwartungswerts von einem Wert der von eine Zufallsvariable im Mittel angenommen wird.

Zum Beispiel können wir den Würfelwurf eines fairen Würfels betrachten. Die Zufallsvariable wäre in diesem Fall die Augenzahl des Würfelwurfs. Nehmen wir an wir Würfeln fünfmal und erhalten 1, 4, 1, 1, 2. In diesem Fall wäre der Mittelwert gleich

\[ (1+4+1+1+2) / 5 = 1.8 \]

Der Erwartungswert ist jedoch die Summe jeder möglichen Augenzahl multipliziert mit dessen Eintrittswahrscheinlichkeit:

\[ (1+2+3+4+5+6) \cdot 1/6 = 21/6 = 3.5 \]

Es gibt jedoch einen wichtigen Zusammenhang zwischen Mittelwert und Erwartungswert. Je häufiger wir Würfeln, desto genauer nähert sich der Mittelwert dem Erwartungswert an. Diesen wichtigen Zusammenhang gibt uns das sogenannte Gesetz der großen Zahlen, welches Sie in der Wahrscheinlichkeitstheorie noch kennenlernen werden.

• Lassen wir unseren Roboter einmal laufen und zählen die benötigten Schritte, wissen wir wie viele Schritte er für genau diesen einen Lauf gebraucht hat.

• Lassen wir unseren Roboter \(n\) mal laufen und berechnen den Mittelwert der benötigten Schritte, wissen wir wie viele Schritte er für diese \(n\) Läufe durchschnittlich gebraucht hat.

• Lassen wir dieses \(n\) immer größer und größer werden nähern wir uns dem Erwartungswert und können einschätzten wie viele Schritte der Roboter im Mittel generell benötigt.

Im obigen Beispiel mit dem Würfelwurf, haben wir den Erwartungswert analytisch berechnet. Prinzipiell bieten sich also zwei Möglichkeiten den Erwartungswert zu bestimmen:

1. Analytisch, d.h., wir nutzen die Mathematik, genauer gesagt die Wahrscheinlichkeitstheorie, um das Ergebnis analytisch herzuleiten

2. Experimentell, d.h., wir nutzten den Computer und probieren das ganze einfach aus

Analytisch ist die Frage nach der erwarteten Anzahl der benötigten Schritte des Roboters schwer zu lösen.

Exercise 20.13 (Wahrscheinlichkeiten)

Bestimmen Sie für ein \(5 \times 5\) Gebiet die Wahrscheinlichkeit dafür, dass der Roboter nach einem Schritt am Ziel angekommen ist. Der Roboter startet in der Mitte des Gebiets.

Solution to Exercise 20.13 (Wahrscheinlichkeiten)

Diese noch recht einfach anmutende Frage ist schon nicht ganz leicht analytisch zu lösen. Die Wahrscheinlichkeit, dass der Roboter in eine der vier Himmelsrichtungen läuft ist identisch und liegt bei

\[ 1/4. \]

Wir benötigen noch die Wahrscheinlichkeit, dass das Ziel in einer der vier Zellen liegt. Da das Ziel mit gleicher Wahrscheinlichkeit in eine der Zellen (die Zelle des Roboter ausgenommen) fällt, ergibt sich hierfür

\[ 4 / (5 \cdot 5 - 1) = 4 / 24 = 1 / 6 \]

Damit liegt die Wahrscheinlichkeit, dass der Roboter nur einen Schritt benötigt bei

\[ 1 / 6 \cdot 1 / 4 = 1 / 24 \]

Sie können auch argumentieren, dass der Roboter zuerst zieht und wir das Ziel dann setzten. Das Ziel muss genau auf die eine Zelle gesetzt werden, in der der Roboter ist. Das heißt es muss 1 aus 24 möglichen Zellen sein.

Um die Frage nach den erwarteten Schritten zum Ziel experimentell zu lösen, müssen wir viele Experimente bzw. Simulationen machen und zählen wie viele Schritte der Roboter gebraucht hat. Seien \(s_1, \ldots, s_n\) die Schritte für die Experimente \(1\) bis \(n\) dann ist der Mittelwert gegeben durch

\[\frac{1}{n} \sum_{i=1}^n s_i = \frac{1}{n} (s_1 + \ldots + s_n)\]

Exercise 20.14 (Experimente)

Implementieren Sie eine Funktion experiment(nrows, ncols) die

1. eine neue Welt mit nrows Zeilen und ncols Spalten erzeugt,

2. den Roboter zum Ziel führt und

3. die Anzahl der benötigten move()-Aufrufe zurückgibt (passen Sie random_walk(robo) entsprechend an).

Rufen Sie bevor Sie den random_walk(robo) ausführen world.disable_animation() und robo.disable_print() auf. Die erste Methode deaktiviert die Animation der Welt und die zweite die Ausgabe der Roboteraktionen. Dies spart Rechnerressourcen während der Berechnung.

Implementieren Sie sodann eine Funktion experiments(nrows, ncols, n) welche n-mal experiment(nrows, ncols) aufruft und den Durchschnitt berechnet.

Show code cell source Hide code cell source

def experiment(nrows, ncols):
    world = rw.new_world(nrows=nrows, ncols=ncols)
    world.disable_animation()
    robo = world.robo
    robo.disable_print()
    return random_walk(robo)

def experiments(nrows, ncols, n):
    mean = 0
    for _ in range(n):
        mean += experiment(nrows, ncols)
    return mean / n

mean = experiments(nrows=7, ncols=7, n=50)
print(mean)

131.12

Um ein Gefühl für den Erwartungswert zu erlangen können wir nun den Durchschnitt für unterschiedliche n bestimmen.

Exercise 20.15 (Entwicklung des Durchschnitts)

Berechnen Sie für jeden Eintrag n in x

x = list(range(1,401,1))

die durchschnittliche Länge des Roboterlaufs für ein \(5 \times 5\) Gebiet (ncols=5, nrows=5), d.h., bestimmen Sie experiments(5, 5, n).

Speichern Sie all diese Durchschnitte in y ab und lassen Sie sich die Daten durch

import matplotlib.pyplot as plt
plt.plot(x, y, 'bo', markersize=2.5, alpha=0.5)

plotten. Was beobachten Sie?

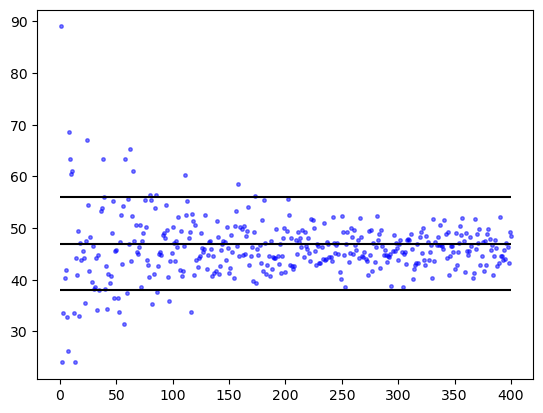
Erst generieren wir mit

nmax = 400
x = list(range(1,nmax+1,1))
y = [experiments(5, 5, n) for n in x]

die Daten und dann plotten wir sie

import matplotlib.pyplot as plt
plt.plot(x, y, 'bo', markersize=2.5, alpha=0.5)
plt.hlines([38, 38 + (56-38)/2, 56], xmin=0, xmax=nmax, colors='black')

<matplotlib.collections.LineCollection at 0x11c4ba850>

Mit

plt.hlines([38, 38 + (56-38)/2, 56], xmin=0, xmax=nmax, colors='black')

<matplotlib.collections.LineCollection at 0x11c56c510>

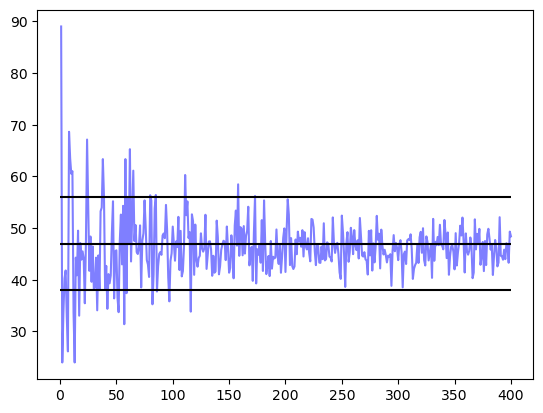
haben wir zwei horizontale Linien bei \(y = 38\), \(y = 38+(56-38)/2\) und \(y = 56\) eingezeichnet um zu verdeutlichen, dass der Erwartungswert mit hoher Wahrscheinlichkeit in dem Interval \([38;56]\) liegt und der Mittelpunkt \(38+(56-38)/2 = 47\) ein erster Schätzwert ist.

Wir beobachten außerdem, dass die Berechnung einige Zeit in Anspruch nimmt und sich der Durchschnitt für größer werdende n einem bestimmten Wert (dem Erwartungswert) zu nähern scheint.

Exercise 20.16 (Plotten mit matplotlib)

Sehen Sie sich die Dokumentation der Funktion plt.plot() an und finden Sie heraus was die einzelnen Argumente des obigen Aufrufs

plt.plot(x, y, 'bo', markersize=2.5, alpha=0.5)

bewirken bzw. bedeuten.

Solution to Exercise 20.16 (Plotten mit matplotlib)

• x und y bestimmen die Datenpunkte, d.h. der i-te Punkt ist definiert durch (x[i], y[i]).

• 'bo' besagt, dass der Plot in in blauer Farbe 'b' gezeichnet wird und dass kreisförmige Marker verwendet werden sollen 'o'.

• Die größe der Marker wird durch marksize=2.5 festgelegt.

• alpha = 0.5 besagt, dass der Plot zu 50 % transparent gezeichnet werden soll.

Exercise 20.17 (Plotten mit matplotlib)

Erzeugen Sie einen identischen Plot wobei dieser keine Marker dafür aber eine Funktionslinie enthalten soll.

Show code cell source Hide code cell source

import matplotlib.pyplot as plt
plt.plot(x, y, 'b-', markersize=2.5, alpha=0.5)
plt.hlines([38, 38 + (56-38)/2, 56], xmin=0, xmax=nmax, colors='black')

<matplotlib.collections.LineCollection at 0x11c6ac790>

Solche Berechnungen in Form von Experimenten/Simulationen werden oft durchgeführt, wenn keine analytische Lösung bekannt ist oder sie gar nicht erst existiert. Beim Suchen einer analytischen Lösung kann dies auch ein sehr hilfreiches Mittel sein um einerseits eine Idee von der Lösung zu bekommen und andererseits seine Vermutung zu untermauern. Ganz nach dem Motto: Habe ich mich verrechnet?

Den Erwartungswert der notwendigen Schritte des Zufallslaufs zu bestimmen ist eine schwierige Aufgabe, der Sie wahrscheinlich noch nicht gewachsen sind. Dennoch können wir als Computational Thinker*innen den Computer verwenden um durch (oft massiv viele) Berechnungen einen guten Schätzwert zu bestimmen. Die oben durchgeführte Methode gehört zu den sog. Monte-Carlo-Simulationen.

Natürlich brauchen wir für derartige Berechnungen viel Rechenleistung und damit auch viel Energie - sie sind nicht kostenlos!

Exercise 20.18 (Berechnungskosten)

Wie häufig haben wir die Roboter der Experimente ungefähr bewegt. Anders gefragt: Wie oft haben wir move() insgesamt aufgerufen?

1. Schätzen Sie erst selbst ab und

2. berechnen Sie es sodann aus y und x.

Unser Schätzwert für den Durchschnitt liegt bei \(47\), d.h. wir können davon ausgehen, dass jedes Experiment \(47\) Schritte benötigt. Wie viele Experimente haben wir durchgeführt? Nun es waren

\[ \sum_{i=1}^{400} i = 1 + 2 + 3 + \ldots + 400 = (400 + 1) + (399 + 2) + \ldots + (201 + 200) = 401 \cdot 200 = 80 200 \]

Insgesamt können wir die Anzahl der Schritte der Roboter mit

\[ 80 200 \cdot 47 = 3 769 400 \]

also ca. 3.7 Millionen abschätzen!

x enthält die Anzahl der Experimente und y die durchschnittliche Anzahl an Roboterschritten. Damit berechnet folgender Code die gesamte Anzahl an Schritten:

Show code cell source Hide code cell source

overall_steps = 0
for i in range(len(x)):
    overall_steps += x[i] * y[i]
print(overall_steps)

3686477.0

Ein etwas besser lesbarer Code entsteht, wenn wir die Python Funktion zip verwenden:

Show code cell source Hide code cell source

overall_steps = 0
for n, mean in zip(x,y):
    overall_steps += n * mean
print(overall_steps)

3686477.0

Die tatsächliche Anzahl steps_sum an Schritten kann etwas geringer oder etwas größer als unsere Abschätzung sein. Wir haben uns um abs(steps_sum - 3_769_400) / steps_sum Prozent verschätzt.

Haben Sie die Aufgabe Exercise 20.13 analytisch lösen können? Lassen Sie uns experimentell nachprüfen ob unsere Berechnungen stimmen!

Exercise 20.19 (Ein Schritt und ich bin da)

Berechnen Sie experimentell eine gute Schätzung für die Wahrscheinlichkeit, dass der Roboter in einem Schritt in einem Gebiet mit 5 Zeilen und 5 Spalten am Ziel angekommen ist.

Show code cell source Hide code cell source

def random_move(robo):
    random_turn(robo)
    robo.move()

def experiment(nrows, ncols):
    world = rw.new_world(nrows=nrows, ncols=ncols)
    world.disable_animation()
    robo = world.robo
    robo.disable_print()
    random_move(robo)
    return robo.is_at_goal()

n = 100_000

count = 0
for _ in range(n):
    if experiment(5, 5):
        count += 1
print(f'Schätzwert: {count/n}, tatsächlicher Wert:{1/24}')

Schätzwert: 0.04209, tatsächlicher Wert:0.041666666666666664

Wir zählen die Anzahl der Läufe für die der Roboter mit nur einem zufälligen Schritt (random_move(robo)) am Ziel ist. Da die Wahrscheinlichkeit für dieses Ereignis sehr klein ist, benötigen wir viele Experimente. Um diese in akzeptabler Zeit durchführen zu können, brechen wir nach dem ersten Schritt des Roboters ab! Das Ergebnis deutet stark darauf hin, dass wir uns nicht verrechnet haben.

Dieses Beispiel zeigt, wie Computer Sie bei Ihrer Denkarbeit unterstützten können. Durch eine Vielzahl an Berechnungen liefert Ihnen der Computer Hinweise zur Lösung eines Problems.

20.4.2. Determinierter Lauf

Als nächstes sollen Sie das gleiche Gebiet determiniert (ohne Zufall) durchlaufen.

Determiniertheit und Determinismus

Die Begriffe determiniert und deterministisch haben in der Informatik eine ganz bestimmte Bedeutung, welche wir nur allzu gerne verwechseln.

• Ein determinierter Algorithmus erzeugt bei gleicher Eingabe auch die gleiche Ausgabe.

• Für einen deterministischer Algorithmus ist während seiner Ausführung zu jedem Zeitpunkt die nächste Anweisung eindeutig definiert.

Die Zufallsfahrt ist aus unserer Sicht nicht determiniert, da Sie bei jeder Ausführung einen anderen Pfad berechnet. Es sei jedoch erwähnt, dass der Lauf auf Pseudozufallsvariablen beruht. Würden wir jede Eingabe (auch den sog. Seed des Pseudozufallsgenerators) kennen, wäre jeder Lauf aus unserer Sicht determiniert und würde mit einer anderen Eingabe starten. Echten Zufalls gibt es auf dem digitalen Computer nicht.

Die Zufallsfahrt ist ineffektiv, wenn es unser Ziel ist mit so wenig Schritten wie möglich zum Ziel zu kommen. Wir besuchen die gleiche Zelle unter Umständen viele Male. Wir haben keine Gewissheit wie lange es für einen bestimmten Lauf dauern mag. Lassen Sie uns nun eine Lauf zum Ziel entwickeln, für den wir eine feste Obergrenze an Schritten feststellen können.

Exercise 20.20 (Determinierter Lauf)

1. Gehen Sie weg vom Rechner und überlegen Sie sich einen Algorithmus der den Roboter sicher ans Ziel des rechteckigen Gebiets ohne Hindernisse führt.

2. Implementieren Sie eine Funktion determined_walk(robo), die den Roboter ohne eine Zufallskomponente für alle möglichen rechteckigen Welten ohne Steine und Hindernisse ins Ziel führt.

3. Bestimmen Sie wie viele Schritte höchstens (worst-case) sowie mindestens (best-case), abhängig von der Größe des Gebiets, nötig sind.

Es gibt viele verschiedene Lösungen für diese Aufgabe. Wir haben uns für einen Zig-Zag-Lauf entschieden:

---
tags: [hide-input]
---
Bewege den Roboter ganz nach Nordwesten.
Laufe jede Spalte ab:
    laufe nach Süden
    laufe einen Schritt nach Osten
    laufe nach Norden 
    laufe einen Schritt nach Osten
    ...

Wir verlagern das Laufen ganz nach Westen/Norden/Süden in Funktionen wie auch der Lauf nach Nordweste walk_north_west().

Show code cell source Hide code cell source

def walk_to_wall(robo, condition = lambda robo: True):
    while not robo.is_wall_in_front() and condition(robo):
        robo.move()

def walk_west(robo, condition = lambda robo: True):
    turn_west(robo)
    walk_to_wall(robo, condition)
    
def walk_north(robo, condition = lambda robo: True):
    turn_north(robo)
    walk_to_wall(robo, condition)

def walk_south(robo, condition = lambda robo: True):
    turn_south(robo)
    walk_to_wall(robo, condition)
    
def walk_north_west(robo, condition = lambda robo: True):
    walk_west(robo, condition)
    walk_north(robo, condition)

def determined_walk(robo):
    condition = lambda robo: not robo.is_at_goal()
    
    walk_north_west(robo, condition)
        
    down = True
    while not robo.is_at_goal():
        if down:
            walk_south(robo, condition)
        else:
            walk_north(robo, condition)
        turn_east(robo)
        if not robo.is_at_goal() and not robo.is_wall_in_front():
            robo.move()
        down = not down

Zudem passen wir walk_to_wall(robo, condition) so an, dass der Lauf abgebrochen wird sobald die condition nicht länger erfüllt ist. In unserem Fall ist diese condition genau dann nicht mehr erfüllt, sobald der Roboter das Ziel erreicht hat. condition ist ein Funktion, welche als Argument den Roboter entgegennimmt und einen Wahrheitswert zurückgibt. Definieren wir keine condition ist der Wahrheitswert immer True.

Lassen Sie uns diesen Code testen.

nrows = 11
ncols = 11
world = rw.new_world(nrows=nrows, ncols=ncols)
robo = world.robo
world.show()

Für ein Gebiet mit \(m\) Zeilen und \(n\) Spalten benötigt unser Algorithmus mindestens einen und höchstens

\[ n \cdot m + \left \lceil{m/2}\right \rceil + \left \lceil{n/2}\right \rceil \]

Schritte, wobei \(\left \lceil{\cdot}\right \rceil\) gleich dem Aufrunden auf die nächste ganze Zahl darstellt.

Das animierte Ergebnis sieht wie folgt aus

Abb. 20.3 Ein determinierter Lauf zum Ziel.

Erneut ergeben sich interessante Fragen:

Gibt es einen Algorithmus der den Roboter (für ein beliebiges Gebiet) so bewegt, dass wir jede Zelle nur maximal einmal durchlaufen müssen?

Wenn nein, gibt es einen Algorithmus der dies für bestimmte Gebiete erzielt?

Exercise 20.21 (Perfekter Lauf)

Geben Sie ein Gebiet an und beschreiben Sie dazu einen geeigneten Algorithmus der jede Zelle nur einmal besucht. Die Zelle auf der Ihr Roboter startet gilt als bereits besucht.

Solution to Exercise 20.21 (Perfekter Lauf)

Nehmen wir das \(3 \times 3\)-Zellen Gebiet:

In diesem Fall können wir nach Westen laufen und dann einmal rund herum und haben jede Zelle nur einmal besucht. Tatsächlich funktioniert diese Strategie für alle \(n \times n\) Gebiete!

Exercise 20.22 (Unmöglicher Lauf)

Geben Sie ein Gebiet an für das es nicht möglich ist jede Zelle nur einmal zu durchlaufen.

Solution to Exercise 20.22 (Unmöglicher Lauf)

Ein einfaches Gegenbeispiel ist jedes \(1 \times n\) für \(n \geq 2\) Gebiet.

Können Sie unseren Algorithmus aus der Lösung (Exercise 20.21) implementieren?

Exercise 20.23 (Perfekter Lauf im Quadrat)

Implementieren Sie eine Funktion determined_walk_square(robo) die den Roboter ohne eine Zufallskomponente für alle möglichen quadratischen Welten ohne Steine und Hindernisse ins Ziel führt und jede Zelle maximal einmal besucht. Die Funktion sollte die Anzahl der benötigten Schritte zurückgeben.

Hinweis: Wir empfehlen erneut vom Rechner weg zu gehen und sich erst einmal mit Stift und Papier zu überlegen welche Roboterbewegungen nötig sind und in welches Muster diese fallen.

Bisher haben wir uns nichts während des Laufens gemerkt. Der Zustand des Roboters wurde lediglich durch seine Ausrichtung beschrieben. Dies ändert sich nun!

Gilt für unser \(n \times n\)-Gebiet, dass \(n\) eine gerade Zahl ist so befindet sich der Roboter nicht genau in der Mitte des Gebiets. Er befindet sich eine Zelle weiter im Norden als im Süden und eine Zelle weiter im Osten als im Osten! Deshalb laufen wir mit dem ersten Schritt immer erst nach Westen und dann nach Süden, sodass wir gegen den Uhrzeigersinn laufen!

Zwischen der Drehung nach links (turn_left()) und den Schritten (move()) können wir folgenden Zusammenhang feststellen: Die Anzahl der Schritte erhöht sich nach jeder zweiten Drehung um eins.

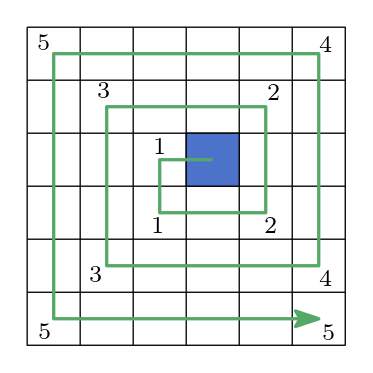
Abb. 20.4 Spirallauf: die Anzahl der move()-Aufrufe erhöht sich um eins nach jedem zweiten turn_left().

Wir müssen nun noch darauf achten, dass wir nicht übers Ziel hinauslaufen. Das ist auch schon alles.

def determined_walk_square(robo):
    steps = 0
    moves = 1
    turn_west(robo)
    while not robo.is_at_goal():
        for _ in range(2):
            for _ in range(int(moves)):
                if not robo.is_at_goal():
                    robo.move()
                    steps += 1
                else:
                    break
            robo.turn_left()
        moves += 1
    return steps

Lassen Sie es uns testen:

nrows = 10
ncols = 10
world = rw.new_world(nrows=nrows, ncols=ncols)
robo = world.robo
robo.disable_print()
world.show()
steps = determined_walk_square(robo)
assert nrows * ncols > steps
print(world.is_successful())

rw.animate(world)

True

Once Loop Reflect

20.4.3. Eine künstliche Intelligenz (optional)

Bis hierher haben wir Algorithmen entwickelt um unseren Roboter sicher durch eine teilweise bekannte Welt zu bewegen. Wir wussten zwar nicht exakt wie diese Welt aussieht jedoch wussten wir, dass sie zum Beispiel keine Hindernisse oder Steine enthält. Oder wir wussten, dass unser Gebiet rechteckig ist. Zudem wussten wir wo der Roboter startet (in der Mitte bzw. ganz im Westen).

Ändern wir die Perspektive und versetzten uns in den Roboter hinein. Nehmen wir an wir wissen rein gar nichts über das Gebiet. Wir kennen nur unseren, d.h. den Zustand des Roboters selbst. Bewegen wir uns, können wir uns natürlich merken, wohin wir uns bewegt haben und wie die Welt dort aussah. Wir können die Welt erkunden und so Unsicherheiten auflösen, in anderen Worten, wir können Informationen durch Erkundungen einholen.

Lassen wir verrückbare Steine außer acht. Die Welt in der der Roboter sein Ziel finden muss ist eine Welt voller unverrückbarer Hindernisse. Wir wissen weder wo der Roboter startet noch wie die Welt genau aussieht. Der Roboter soll selbst den Weg durch Erkundung finden!

20.4.3.1. Aufzählen aller möglichen Läufe

Da wir absolut kein Wissen über das Gebiet haben, werden wir alle nur möglichen Läufe/Wege ausprobieren. Erinnern Sie sich an den Zufallslauf! Auch hier haben wir im Grunde alle möglichen Läufe durchprobiert allerdings mehrfach die selben und in chaotischer Reihenfolge. Was wir zunächst benötigen ist ein Algorithmus, der uns alle möglichen Läufe auflisten kann.

Zunächst ist festzustellen, dass jeder Lauf eine Folge von Schritten move() und Linksdrehungen turn_left() ist. Zum Beispiel besuchen wir mit

move(), turn_left(), turn_left(), move(), move().

drei Zellen (die Startzelle ausgeschlossen) und die Platzierung der Drehungen turn_left() in der Folge entscheidet bei welcher Zelle wir ankommen. So können wir leicht alle möglichen Läufe mit drei move() Befehlen auflisten:

1. move(), move(), move()

2. move(), move(), turn_left(), move()

3. move(), move(), turn_left(), turn_left(), move()

4. move(), move(), turn_left(), turn_left(), turn_left(), move()

5. move(), turn_left(), move(), move()

6. move(), turn_left(), move(), turn_left(), move()

7. move(), turn_left(), move(), turn_left(), turn_left(), move()

8. move(), turn_left(), move(), turn_left(), turn_left(), turn_left(), move()

9. move(), turn_left(), turn_left(), move(), move()

10. …

20.4.3.2. Repräsentation der Läufe

Wir können hierfür eine andere, kürzere und besser handhabbare Repräsentation/Codierung wählen, indem wir lediglich die Anzahl der turn_left() vor jedem move() notieren. Wir lassen überflüssige Informationen weg:

1. 000

2. 001

3. 002

4. 003

5. 010

6. 011

7. 012

8. 013

9. 020

10. …

Erinnert Sie das an etwas?

Exercise 20.24 (Anzahl möglicher Läufe)

Wie viele Unterschiedliche Läufe der Länge drei (drei mal move()) gibt es?

Solution to Exercise 20.24 (Anzahl möglicher Läufe)

Es gibt

\[ 4^3 = 64 \]

mögliche Läufe!

Einige Läufe besuchen teilweise die gleichen Zellen. Zum Beispiel

• move(), move(), move() bzw. 000 und

• move(), move(), turn_left(), turn_left(), move() bzw. 002.

Auch gibt es Läufe die auf der gleichen Zelle enden. Darum kümmern wir uns später noch.

Von hier an verwenden wir für die Schreibweise eines Laufs die Codierung durch Zahlen.

Oben haben wir alle Läufe der Länge drei in einer bestimmten Art und Weise aufgelistet! Wir starten mit 000 was als Dezimalzahl die 0 ist und addieren für jeden nächsten Lauf eins drauf:

1. 000

2. 000 + 001 = 001

3. 001 + 001 = 002

4. 002 + 001 = 003

5. 003 + 001 = 010

6. …

20.4.3.3. Tiefen- und Breitensuche

Hmm Moment einmal, wir wissen ja nicht wie oft wir den Roboter nach vorne bewegen können? Es befinden sich Hindernisse im Gebiet, welche bestimmte Möglichkeiten ausschließen. Das macht nichts, denn in diesem Fall lassen wir diesen Lauf einfach aus.

Auch kennen wir die Länge der Läufe nicht. Auch das ist kein Problem, wir laufen solange bis es einfach nicht mehr weiter geht oder wir unser Ziel gefunden haben. Zum Beispiel wird unser erster möglicher Lauf \(n\) Nullen enthalten, wobei \(n\) die Anzahl der Schritte ist, welche wir den Roboter laufen lassen können bis er an ein Hindernis stößt.

Die oben gewählte Reihenfolge in der wir die Läufe auflisten nennt man Tiefensuche (engl. depth-first search). Wir können aus den Läufen einen Baum konstruieren wobei jeder Lauf eine Durchwanderung des Baums von der Wurzel zu einem Kind darstellt. Jeder Knoten hat genau 4 Kanten:

• eine Kante für 0

• eine für 1

• eine für 2

• eine für 3

Jeder Lauf ist durch ein Blatt (Knoten ohne Kinder) definiert. Der Baum ist für Läufe der Länge 2 in Abbildung 20.5 skizziert.

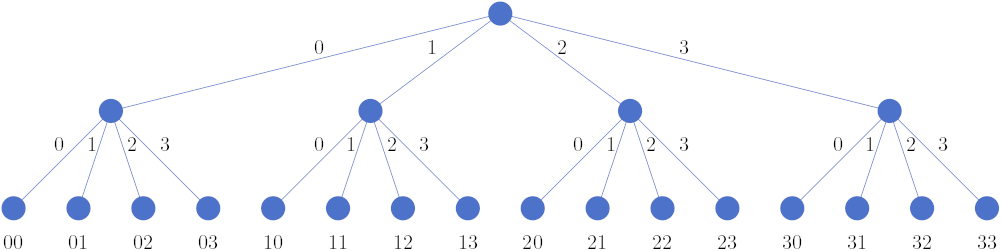
Abb. 20.5 Ein Baum der alle möglichen Läufe der Länge zwei codiert.

Tiefensuche durchwandert einen Baum, sodass wann immer ein Kindknoten noch nicht besucht wurde, dieses besucht wird. In anderen Worten wir gehen erst tief in den Baum hinein und springen erst wieder nach oben, wenn alles darunter bereits besucht wurde. Zudem wandern wir meist von links nach rechts.

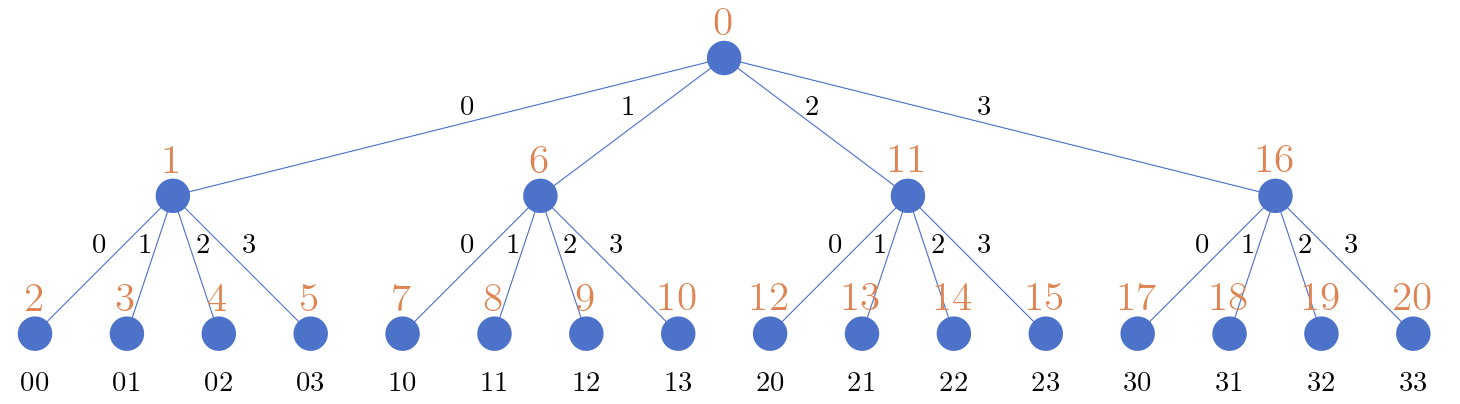
Abb. 20.6 Tiefensuche des Baums in Abbildung 20.5. Die orangen Zahlen geben die Reihenfolge vor.

Ein anderer Algorithmus, der einen Baum durchwandert, ist die sogenannte Breitensuche (engl. breadth-first search). Hierbei gehen wir erst in die nächst tiefere Ebene, wenn alle Knoten der aktuellen Ebene bereits besucht wurden. Vergleichen Sie folgende Abbildung.

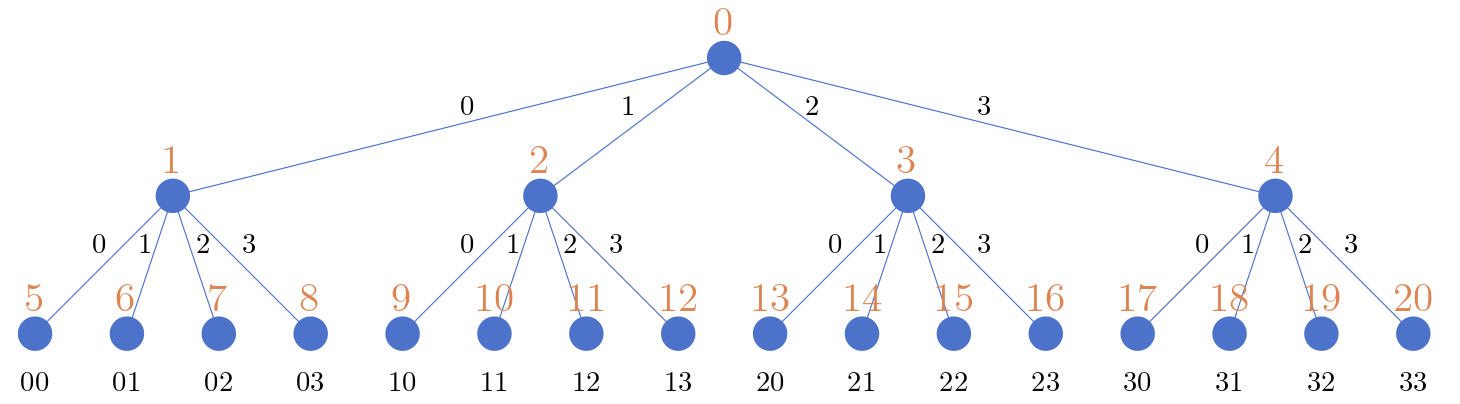
Abb. 20.7 Breitensuche des Baums in Abbildung 20.5. Die orangen Zahlen geben die Reihenfolge vor.

20.4.3.4. Inverse Operationen

Um nun eine der beiden Suchalgorithmen als einen Roboterlauf zu implementieren haben wir noch ein Problem! Wir können nicht so einfach von z.B. 03 nach 10 gehen. Wann immer wir von einem Knoten wieder nach oben im Baum laufen, müssen wir auch mit dem Roboter den gelaufenen Weg zurücklaufen! Deshalb benötigen wir für jede Kombination aus Drehungen und Schritt nach vorne laufen, die inverse Operation: Laufe zurück und richte den Rober so aus, wie er zuvor ausgerichtet war.

Exercise 20.25 (Inverse Operation)

Was ist die inverse Operation von 1? Anders gefragt, durch welche Folge von move() und turn_left() gelangt man im Baum von z.B. 0031 zu 003?

Solution to Exercise 20.25 (Inverse Operation)

1 bedeutet turn_left(), move().

Durch turn_left(), turn_left() (bzw. turn(robo)) und move(), was im übrigen der 2 entspricht, laufen wir zurück. Um nach einer Linksdrehung wieder zum Ausgangspunkt zu kommen, benötigen Sie drei Linksdrehungen. Da wir den Roboter beim Zurücklaufen bereits zweimal gedreht haben fehlt noch ein turn_left().

Exercise 20.26 (Codierung in Operationen übersetzten)

1. Schreiben Sie eine Funktion move_back(robo), die den Roboter zurück bewegt (und die vorherige Ausrichtung wieder herstellt).

2. Schreiben Sie eine Funktion move(robo, code), welche den Roboter so bewegt wie es der code 0, 1, 2 oder 3 vorgibt.

3. Schreiben Sie eine Funktion inverse_move(robo, code), welche den Roboter so bewegt, dass die Bewegung, welche durch code vorgegeben ist, rückgängig gemacht wird.

Annahme: Ignorieren Sie zunächst, dass eine move() Operation möglicherweise wegen einem Hindernis nicht durchführbar ist.

Show code cell source Hide code cell source

def move_back(robo):
    turn(robo)
    robo.move()
    turn(robo)
    
def move(robo, code):
    for _ in range(code):
        robo.turn_left()
    robo.move()
    
def inverse_move(robo, code):
    move_back(robo)
    for _ in range(4-code):
        robo.turn_left()

Sofern wir die inversen Operationen an der richtigen Stelle aufrufen, können diese nicht schiefgehen. Der Roboter kommt schließlich von der Zelle zu der wir zurücklaufen. Anders verhält es sich jedoch mit move(robo, code)! Diese Funktion kann in einem Fehler enden, sofern nach der Drehung ein Hindernis vor uns steht.

Exercise 20.27 (Codierung in Operationen übersetzten (verbessert))

Ändern Sie move(robo, code) so ab, dass die Operationen des Roboters entweder ganz oder gar nicht duchgeführt werden. Die Funktion soll zudem True zurückgeben, falls die Operationen durchführbar waren und sonst False zurückliefern.

Show code cell source Hide code cell source

def move(robo, code):
    for _ in range(code):
        robo.turn_left()
    if robo.is_wall_in_front():
        for _ in range((4-code)%4):
            robo.turn_left()
        return False
    else:
        robo.move()
        return True

20.4.3.5. Kreise verhindern

Ein Problem existiert noch immer! Bereits für einen einfachen Korridor mit zwei Zellen ist der Baum der Läufe unendlich groß. Wir können immer vor und zurük laufen, also zum Beispiel: 02020202020202020…

Auch wenn wir diese eine Möglichkeit verhindern, so besteht immer die Gefahr, dass wir im Kreis herumlaufen. Wir müssen uns merken, welche Zelle wir bereits besucht haben, sodass wir den Baum nur weiter durchsuchen, falls die entsprechende Zelle noch nicht besucht wurde. Hierfür stellen wir Ihnen die folgenden beiden Methoden zur Verfügung:

1. robo.set_mark(): Setzt eine Markierung auf die Zelle auf der der Roboter gerade steht.

2. robo.is_mark_in_front(): Gibt True zurück sofern sich vor dem Roboter eine markierte Zelle befindet, sonst False.

Exercise 20.28 (Codierung in Operationen übersetzten (verbessert\(^2\)))

Ändern Sie move(robo, code) so ab, dass Sie keine Zelle doppelt besuchen.

Show code cell source Hide code cell source

def move(robo, code):
    for _ in range(code):
        robo.turn_left()
    if robo.is_wall_in_front() or robo.is_mark_in_front():
        for _ in range((4-code)%4):
            robo.turn_left()
        return False
    else:
        robo.move()
        robo.set_mark()
        return True

Sie haben nun im Grunde alles was Sie brauchen um die Tiefensuche zu implementieren. Das ist nicht ganz einfach! Bedenken Sie, dass Sie nicht genau wissen wie der Baum aussieht den Sie durchsuchen. Wir empfehlen Ihnen erst einmal an einem Beispielbaum mit Stift und Papier zu überdenken, in welcher Art und Weise Sie diesen durchlaufen können. Was müssen Sie sich während des Laufs merken? Wie gelangen Sie tiefer hinein, wie nach rechts und wie wieder nach oben? Wann wissen Sie, dass es keinen Weg zum Ziel gibt?

Exercise 20.29 (Tiefensuche des Roboters (schwer!))

Implementieren Sie nun die Tiefensuche depth_first_walk(robo) welche den Roboter zum Ziel führt und eine Liste zurückgibt, welche den Pfad im Suchbaum darstellt. Falls es keinen Weg zum Ziel gibt, so sollte diese Funktion eine leere Liste zurückgeben.

Show code cell source Hide code cell source

def depth_first_walk(robo):
    path = []
    code = 0
    # try until robo is at goal
    while not robo.is_at_goal():
        # try the current code
        if move(robo, code):
            path.append(code)
            code = 0
        else:
             # walk up in the tree as long as necessary
            if code == 3:                
                while len(path) > 0 and path[-1] == 3:
                    parent = path.pop()
                    inverse_move(robo, parent)
                    print(path)
                    
                # the goal is not reachable
                if len(path) == 0:
                    return path
                parent = path.pop()
                inverse_move(robo, parent)
                
                code = parent + 1
            else:
                code += 1
    return path

Exercise 20.30 (Inverselauf des Roboters)

Implementieren Sie eine Funktion inverse_walk(robo, path) welche den Roboter zurück an seine Ausgangsposition bringt.

Show code cell source Hide code cell source

def inverse_walk(robo, path):
    for i in range(len(path)-1, -1, -1):
        inverse_move(robo, path[i])

Exercise 20.31 (Lauf wiederholen)

Implementieren Sie eine Funktion walk(robo, path) welche den Lauf path ausführt, sodass fogender Code den Roboter erst zum Ziel führt, dann wieder zurücklaufen lässt und schlussendlich erneut zum Ziel führt:

path = depth_first_walk(robo)
inverse_walk(robo, path)
walk(robo, path)

Show code cell source Hide code cell source

def walk(robo, path):
    for code in path:
        for _ in range(code):
            robo.turn_left()
        robo.move()

Exercise 20.32 (Lauf im Labyrinth)

Testen Sie ihre Funktionen an dem Labyrinth, was Sie sich durch

world = rw.maze()
world.show()

erzeugen können.

world = rw.maze()
robo = world.robo
robo.disable_print()
path = depth_first_walk(robo)
assert world.is_successful()
inverse_walk(robo, path)
walk(robo, path)
assert world.is_successful()
inverse_walk(robo, path)
walk(robo, path)
assert world.is_successful()

rw.animate(world)

Once Loop Reflect

Exercise 20.33 (Breitensuche)

Wir könnten auch eine Breitensuche implementieren. Weshalb eignet sich diese für unsere Roboterläufe nicht so sehr wie die Tiefensuche?

Solution to Exercise 20.33 (Breitensuche)

Mit der Breitensuche würden wir im Schnitt mit dem Roboter deutlich mehr Schritte vollziehen, da wir größere Strecken zurücklaufen müssten und wir viel mehr Zellen doppelt durchlaufen würden.

20.4.3.6. Kürzester Weg

Anstatt irgendeinen Weg zu finden wäre es noch interessant einen Weg zu finden, sodass es keinen anderen Weg gibt der kürzer ist. Einer der bekanntesten Algorithmen für dieses Problem ist der sogenannte Dijkstra-Algorithmus. In unserem Fall handelt es sich jedoch um einen Spezialfall, denn jeder Schritt des Roboters überwindet die gleiche Distanz – er springt von Zelle zu Zelle. Deshalb suchen wir den Pfad der zum Ziel führt und die minimale Anzahl an Zellen besucht.

Exercise 20.34 (Breitensuche und kürzester Weg)

Führen wir die Breitensuche durch und brechen dabei ab sobald wir auf das Ziel stoßen ist der resultierende Weg der kürzeste Weg. Weshalb ist das so?

Solution to Exercise 20.34 (Breitensuche und kürzester Weg)

Die Ebene des Baums ist gleich der Distanz, welche der Roboter gelaufen ist. Da wir immer erst alle oberen Ebenen (also die Wege mit geringer gelaufener Distanz) prüfen bevor wir zur nächst tieferen gelangen, können wir sicher sein, dass der gefundene Lauf der kürzeste ist!

Da der Roboter immer wieder zurücklaufen muss ist die Breitensuche in unserem Fall sehr ineffektiv. Wir können die Breitensuche auf die Tiefensuche reduzieren, d.h. wir können die Breitensuche durch die Tiefensuche lösen. Wie soll das gehen? Wir führen die Tiefensuche nur bis zu einer bestimmten Ebene (Distanz distance) durch.

Nehmen Sie an depth_first_walk(robo, distance=None, unmark=False) führt die Tiefensuche nur bis zu einer Distanz distance durch. Dann würde ein Algorithmus der folgenden Art die Breitensuche realisieren:

distance = 1
while some_condition:
    path = depth_first_walk(robo, distance=distance, unmark=True)
    distance += 1

Führen wir die Tiefensuche jedoch mehrfach durch, müssen wir unsere Welt von den Markierungen befreien. Ansonsten würde der Roboter beim zweiten Aufruf von depth_first_walk() sich bereits nicht mehr bewegen, da er vor lauter markierten Zellen steht. Deshalb haben wir ein weiteres Argument unmark eingefügt. Ist dieses True werden die Markierungen wieder durch robo.unset_mark() gelöscht. unset_mark() löscht eine Markierung der Zelle auf der der Roboter gerade steht.

Wie stellen wir nun jedoch fest, wann es keinen Lauf zum Ziel gibt? Sofern die Funktion depth_first_walk kein Ergebnis zurückliefert sind wir zuvor davon ausgegangen, dass es dann auch keinen Lauf zum Ziel gibt. Laufen wir jedoch nur eine bestimmte Distanz, reicht eine leere Liste als Rückgabewert nicht aus, denn dies signalisiert lediglich, dass es für diese Distanz keinen Weg gibt. Wenn es jedoch keinen Weg gibt, dann ist die erlaubte Distanz distance irgendwann größer als die maximale tatsächlich gelaufene Distanz!

Exercise 20.35 (Beschränkte Tiefensuche (schwer))

Passen Sie Ihre Funktion breadth_first_walk(robo, distance, unmark) so an, dass sie die Tiefensuche nur bis zu einer bestimmten Distanz durchführt. Falls distance == None sollte Ihre Funktion weiterhin die unbeschränkte Tiefensuche durchführen. Falls kein Ziel gefunden wird sollte der Roboter wieder an seiner Startposition stehen. Die Funktion sollte ein Paar zurückgeben (return path, level), wobei level die maximale tatsächlich gelaufene Distanz ist.

Tipps:

1. Anstatt nicht tiefer in den Baum zu gehen falls vor dem Roboter ein Hindernis ist, können Sie auch nicht weiter gehen falls der Lauf schon die Länge gleich distance erreicht hat.

2. Markierungen löschen Sie am besten in der Funktion move_back(robo, unmark=False).

Wir passen zunächst move_back(robo) und inverse_move(robo, code) an:

Show code cell source Hide code cell source

def move_back(robo, unmark=False):
    turn(robo)
    if unmark:
        robo.unset_mark()
    robo.move()
    if unmark:
        robo.unset_mark()
    turn(robo)
    
def inverse_move(robo, code, unmark=False):
    move_back(robo, unmark)
    for _ in range(4-code):
        robo.turn_left()

In der Funktion depth_first_walk(robo) fügen wir die beiden Argumente distance und unmark hinzu und belegen sie mit geeigneten Standardwerten. unmark müssen wir an inverse_move weiterleiten. Ansonsten müssen wir lediglich eine Codezeile ändern! Aus

if move(robo, code):

wird

if (distance == None or len(path) < distance) and move(robo, code):

Wichtig: Die Reihenfolge der logischen Ausdrücke ist hier wichtig denn move(robo, code) bewegt den Roboter bereits. Dies möchten wir jedoch nicht, wenn der Lauf bereits lang genug ist! Deshalb muss (distance == None or len(path) < distance) zuerst ausgewertet werden.

Wann immer die Liste path vergrößert wird, passen wir level durch

level = max(level, len(path))

an.

Show code cell source Hide code cell source

def depth_first_walk(robo, distance, unmark=False):
    path = []
    code = 0
    level = 0
    # try until robo is at goal
    while not robo.is_at_goal():
        # try the current code
        if (distance == None or len(path) < distance) and move(robo, code):
            path.append(code)
            code = 0
            level = max(level, len(path))
        else:
             # path up in the tree as long as necessary
            if code == 3:                
                while len(path) > 0 and path[-1] == 3:
                    parent = path.pop()
                    inverse_move(robo, parent, unmark)
                    
                # the goal is not reachable
                if len(path) == 0:
                    return path, level
                parent = path.pop()
                inverse_move(robo, parent, unmark)
                
                code = parent + 1
            else:
                code += 1
    return path, level

Exercise 20.36 (Berechnung des kürzesten Laufs)

Implementieren Sie mithilfe von depth_first_walk() die Funktion find_shortest_walk(robo), welche Ihnen den kürzesten Lauf zum Ziel zurückliefert. Falls es keinen Lauf zum Ziel gibt, so sollte diese Funktion eine leere Liste zurückliefern.

Wir suchen solange bis:

1. Der zurückgelieferte Lauf nicht leer ist oder

2. Die tatsächlich gelaufene Distanz gleich wie die vorgegebene Beschränkung ist.

Show code cell source Hide code cell source

def find_shortest_walk(robo):
    distance = 1
    level = 0
    path = []
    while len(path) == 0 and distance-1 == level:
        path, level = depth_first_walk(robo, distance=distance, unmark=True)
        distance += 1
    return path

Lassen Sie uns das einmal austesten.

nrows = 10
ncols = 10
world = rw.new_world(nrows=nrows, ncols=ncols)
robo = world.robo
robo.disable_print()
world.disable_animation()
world.show()

path = find_shortest_walk(robo)
print(f'Shortest walk: {path}')
inverse_walk(robo, path)
world.enable_animation()

walk(robo, path)
rw.animate(world)

Shortest walk: [1, 1]

Once Loop Reflect

Da unser Algorithmus viele Tiefensuchen durchführt ist er nicht sonderlich effektiv. Die Ausführung kann einige Zeit in Anspruch nehmen. Wir erkennen jedoch, dass der Algorithmus tatsächlich einen der kürzesten Wege findet.

20.4.3.7. Lauf im Labyrinth

Sie können sich noch eine weitaus komplexere Welt mit Hindernissen erzeugen lassen. Ein echtes Labyrinth! Dazu dient folgender Aufruf:

nrows = 10
ncols = 10
world = rw.complex_maze(nrows,ncols)
world.show()

Es wird Zeit die beiden Läufe, die wir einmal durch die Tiefensuche und einmal durch die Breitensuche berechnen, zu vergleichen. Sie können gerne mit nachfolgendem Code herumspielen.

Zuerst erzeugen wir uns ein Labyrinth und kopieren dieses. Außerdem deaktivieren wir die Ausgabe und die Möglichkeit zu animieren.

import roboworld as rw
import copy

world1 = rw.complex_maze(10, 10)
world2 = copy.deepcopy(world1)
robo1 = world1.robo
robo2 = world2.robo

robo1.disable_print()
robo2.disable_print()

world1.disable_animation()
world2.disable_animation()

world1.show()

Dann generieren wir einen Lauf durch die Tiefensuche, laufen den Lauf wieder zurück, aktivieren die Animation, laufen den Lauf erneut ab und animieren den Lauf.

path1, level1 = depth_first_walk(robo1, distance=None)
inverse_walk(robo1, path1)
world1.enable_animation()
walk(robo1, path1)

rw.animate(world1)

Once Loop Reflect

Der Roboter scheint recht verwirrt durch die Gegen zu laufen. Das gleiche führen wir nun mit der Breitensuche durch.

path2 = find_shortest_walk(robo2)
inverse_walk(robo2, path2)
world2.enable_animation()
walk(robo2, path2)

rw.animate(world2)

Once Loop Reflect

In diesem Fall läuft der Roboter zielstrebig auf kürzestem Weg zum Ziel. Vergleichen Sie den Unterschied!

Es ist anzumerken, dass der Roboter den kürzesten Weg ersteinmal finden musste. Wenn wir die gelaufene Gesamtstrecke vergleichen, ist er durch die Tiefensuche wahrscheinlich insgesamt weniger weit gelaufen.

Exercise 20.37 (Aufwand der Breitensuche)

Angenommen der kürzeste Weg zum Ziel besteht aus 5 Zellen. Wie viele Schritte muss der Roboter maximal insgesamt laufen, wenn wir er durch die Breitensuche bewegt wird?

Solution to Exercise 20.37 (Aufwand der Breitensuche)

Für eine Tiefensuche der Distanz \(k\) benötigt der Roboter

\[ 2 \cdot 4^k \]

Schritte. Wir laufen jede Kante des Baums zweimal ab (Hinweg und Rückweg). Das bedeutet der Roboter läuft insgesamt maximal

\[ 2 \cdot (4^1 + 4^2 + 4^3 + 4^4 + 4^5) = 2728 \]

Schritte.

Zum Vergleich: Die unbeschränkte Tiefensuche braucht für ein Gebiet mit \(n\) Zellen maximal \(2n\) Schritte, denn wir besuchen keine Zelle doppelt müssen aber hin und wieder zurücklaufen. Für ein Gebiet mit 36 Spalten und 36 Zeilen würde die Tiefensuche für den obigen Fall weniger Schritte benötigen (\(36 < \sqrt{2728 / 2}\)).