3.2. Die Formalisierung des Denkens

Mit dem provokanten Titel dieses Abschnitts wollen wir nicht etwa ausdrücken, dass Maschinen oder Algorithmen tatsächlich denken. Vielmehr geht es um die Anstrengung dieses Denken derart zu formalisieren, dass es für bestimmte Operationen nicht mehr notwendig ist. Aus Denken wird Rechnen.

3.2.1. Aristotelische Logik

Dieser Prozess der Formalisierung begann mit der Entwicklung der Logik. Der Begriff Logik stammt vom Griechischen logos was soviel wie Denken, Wort, Gedanke, Sinn oder Rationalität heißt. Und wieder ist es Aristoteles (384-322 v. Chr.) der den Anfang für einen breiteren Durchbruch der Logik machte. Zwar wurde die Kunst der Argumentation bereits bei Sokrates und Plato verwendet aber erst Aristoteles entwickelte ein abgeschlossenes System der Logik und etablierte dieses als wissenschaftliche Disziplin. Seine Beiträge zur Logik finden Sie in seinem Werk Organon aber auch als Teil seiner Metaphysik. Diese Werke stammen ursprünglich nicht von Aristoteles sondern wurden von Andronicus von Rhodes veröffentlicht.

Die Basis für das logische Schlussfolgern oder kurz logische Schließen ist das Denken. Und es wird angenommen, dass dieses Denken, wenn es denn vernünftig ist auch konsistent ist. Eine Schlussfolgerung mag auf Tatsachen d.h. Annahmen und deren gemeinsamen Konzepten zustande kommen. Die Annahmen müssen selbst konsistent sein. Grundannahmen werden dabei als Axiome bezeichnet. Solche Axiome gelten als absolut wahr und benötigen deshalb keines Nachweises in Form eines Beweises. In der Mathematik müssen wir immer mit derartigen Axiomen beginnen. Es gibt keine Möglichkeit jede Annahme in einem System zu beweisen, denn auf irgendwelchen Stelzen muss ein System schließlich stehen. Neben unserem heutigen Verständnis eines Axioms verstand Aristoteles ein Axiom auch als praktisches Grundprinzip.

Mit dem Gesetz der logischen Deduktion können wir aus gegebenen Annahmen wahre Aussagen schließen indem wir aus dem Generellen das Spezielle herausarbeiten. Seinen Syllogismus, verstanden als dreiteilige Schlussfolgerung beschreibt Aristoteles wie folgt: Aus der ersten Hauptprämisse, gefolgt von der Nebenprämisse, folgern wir die Schlussfolgerung. Beide Prämissen enthalten einen gleichen Begriff auch genannt Terminus Medius (M), zum Beispiel ‚Mensch‘. Dieser Begriff bezieht sich auf ein Subjekt (S) welches als Teil einer Menge in der Nebenprämisse auftaucht. Ein Predikat (P) wird der Menge zugewiesen und kann dann in der Schlussfolgerung dem Subjekt zugewiesen werden:

• Alle Menschen (M) sind sterblich (P) (Hauptprämisse)

• Sokrates (S) ist ein Mensch (M) (Nebenprämisse)

• Sokrates (S) ist sterblich (P) (Schlussfolgerung)

Um Wahrheit herauszuarbeiten geht Aristoteles von drei Grundprinzipien aus:

1. Der Satz der Identität besagt, dass ein Gegenstand oder Ding \(A\) zu sich selbst identisch ist, d.h. \(A=A\) ist wahr.

2. Der Satz vom Widerspruch besagt, dass es keine Aussage gibt, welche zugleich wahr als auch falsch ist, d.h. \(A \land \neg A\) ist falsch.

3. Der Satz vom ausgeschlossenen Dritten besagt, dass eine Aussage entweder wahr oder falsch ist, d.h. \(A \lor \neg A\) ist wahr.

Gottfried Wilhelm Leibniz fügte zu diesen Gesetzen noch den Satz vom zureichenden Grund hinzu, der besagt, dass jedes Ereignis eine Ursache haben muss beziehungweise dass es für jede wahre Aussage einen Grund gibt, durch den sie wahr ist. Das heißt, dass jede wahre Aussage durch eine andere Aussage begründet werde, deren Wahrheit bewiesen ist. Somit sind Zirkelschlüsse nicht zulässig. Es finden sich ähnliche Ideen bereits vor Leibniz bei Demokritus (460-371 v. Chr.). Diese vier Sätze begründeten die klassische Logik.

Um zu einer allgemeinen Schlussfolgerung zu gelangen, wendet Aristoteles zwei unterschiedliche Arten der Induktion an: Die unvollkommene Induktion verwendet mehrere spezielle Aussagen um zu einer generellen Aussage zu gelangen. Die Induktion durch Aufzählung beginnt mit dem Beweis einer Charakteristik für eine bestimmte Anzahl an Elementen einer Gruppe, um dann diese Charakteristik als wahr für alle Elemente der Gruppe zu beweisen. Auch Sokrates versuchte durch die Induktion allgemeines Wissen durch die Beobachtung einzelner Fälle herzuleiten.

Es sei an dieser Stelle gesagt, dass die Aristotelische Logik das abendländische Denken lange Zeit besimmte und noch immer bestimmt, doch gab es beispielsweise um 600 v. Chr in der Buddistischen Tradition ähnliche Entwicklungen in Indien.

3.2.2. Antike Algorithmen

Neben der Logik finden wir bei den antiken Griechen auch die ersten erste uns überlieferten Algorithmen. Um 300 v. Chr. notiert Euklid den ersten uns betkannten nicht-trivialen Algorithmus, der heute unter dem Namen euklidischer Algorithmus bekannt ist.

Abb. 3.2 Ein Fragment der Werke Die Elemente, Quelle.

In seinem Werk Die Elemente in Buch VII formulierte er den Algorithmus für positive ganze Zahlen und in Buch X für positive reelle Zahlen. Das Verfahren wurde wahrscheinlich nicht von Euklid erfunden, da er in den Elementen die Erkenntnisse früherer Mathematiker zusammenfasste. Es wird vermutet, dass Buch VII ein schon von den Pythagoreern verwndetes Lehrbuch der Zahlentheorie ist [van de Waerden, 1957]. Für ganze Zahlen berechnet der Algorithmus den größten gemeinsamen Teiler gcd(a,b) zweier natürlicher Zahlen a, b. Über zweitausend Jahre später finden wir jenen Algorithmen in einer anderen Form wieder.

def gcd(a,b):
    """
    Returns the greatest common divisor of a and b.
    """
    while b:
        a, b = b, a % b
    return a

gcd(36, 24)

12

[The Euclidean algorithm] is the granddaddy of all algorithms, because it is the oldest nontrivial algorithm that has survived to the present day. – Donald Knuth, The Art of Computer Programming, Vol 2.

Abb. 3.3 Denker*innen Ihrer Zeit: Euklid, Eratosthenes, Hypatia, Quellen: 2, 3.

Nach Eratosthenes ist ein Algorithmus, das sog. Sieb des Eratosthenes benannt, der zur Berechnung von Primzahlen dient. Allerdings hat auch Eratosthenes, der im 3. Jahrhundert v. Chr. lebte, das Verfahren nicht entdeckt, sondern nur die Bezeichnung ‚Sieb‘ für das schon lange vor seiner Zeit bekannte Verfahren eingeführt.

def sieve_of_eratosthenes(N):
    """
    Returns a list of all prime numbers p in ascending order with p < N.
    """
    N = 100
    prime_sieve = [True for i in range(N)]
    prime_sieve[0] = False
    prime_sieve[1] = False
    for i in range(2, int(N**0.5)):
        if prime_sieve[i]:
            for j in range(i**2, N, i):
                prime_sieve[j] = False
    
    primes = []
    for i in range(N):
        if prime_sieve[i]:
            primes.append(i)
    return primes
        
sieve_of_eratosthenes(100)

[2,
 3,
 5,
 7,
 11,
 13,
 17,
 19,
 23,
 29,
 31,
 37,
 41,
 43,
 47,
 53,
 59,
 61,
 67,
 71,
 73,
 79,
 83,
 89,
 97]

3.2.3. Von der Scholastik zur modernen Logik

Die Stoa entwickelten die Logik weiter indem sie zwischen Objekten, theoretischen Bildern und linguistischen Zeichen unterschieden. Danach verschwand die Aristotelische Logik über lange Zeit und tauchte erst wieder im Mittelalter auf. Die Sekularisierung nahm ihren Lauf und am Ende des 11. Jahrhunderts entstanden aus den Schulen der Klöster und Katedralen die ersten Universitäten.

Die Zeit der Scholastik, welche die Vernunft und den Glauben als Mittel der Wissenserzeugung sah, begann. Die Aristotelische Logik wurde dabei insbesondere durch Thomas von Aquine zu einem inhärenten Bestandteil der scholastischen Logik. Das logische Denken wurde kultiviert, jedoch hauptsächlich als Instrument zur Unterstützung des christlichen Glaubens. Die Scholastik versuchte den Glauben durch logische Schlüsse zu rechtfertigen bzw. zu begründen und zu ergründen.

Diese Entwicklung war der erste Schritt zu einer Systematisierung und Formalisierung der Logik und damit der Systematisierung der Wissenserzeugung und der Manipulation jenes Wissens in unterschiedlicher Art und Weise in einem abgeschlossenen System. Die dadurch eingeführte Abstraktion ist eine notwendige Vorraussetzung für die Entwicklung eines Systems, in dessen Kontext Algorithmen für die Berechnung der Lösung aller möglichen Probleme konstruiert werden können.

Eine Persönlichkeit die hier erwähnt werden sollte ist der Universalgelehrter Gottfried Wilhelm Leibniz (1646-1716). Neben vieler essentieller wissenschaftlicher Beiträge, wollte er das Wissen an sich durch eine Art Universalsprache formalisieren. Diese sollte es ermöglichen jedes wissenschaftliche Problem mittels eines umfassenden Kalküls zu lösen. Nach dem dreißigjährigen Krieg war für ihn diese Vision auch ein Projekt zur transnationalen Verständigung in Europa. Leibniz arbeitete an einer Codierung für alle möglichen wissenschaftlichen Begriffe und an einem Kalkül welches jene Begriffe der Universalsprache durch logische Operationen verbinden sollte. Beispielsweise wurde durch Multiplikation aus einem ‚Ding‘ (\(2\)) ein ‚Seiendes‘ (\(2 \cdot 3\)) und durch eine weitere Multiplikation, ein ‚Mensch‘ (\(2 \cdot 3 \cdot 5\)).

Wenn Gott zählt ensteht eine Welt. – Leibniz

Auch wenn diese Idee für jene Zeit bahnbrechend gewesen ist, bringt sie auch einige Probleme mit sich und hat sich nicht durchsetzen können. Doch ist es heute selbstverständlich so, dass wir auf der digitalen Maschine alles durch Zahlen repräsentieren. Leibniz war seiner Zeit in jedem Fall voraus. In seiner Welt wurden Zahlen zum Instrument um die Welt zu organisieren. Er entwarf ein konkretes System auch wenn dessen Realisierung zum Scheitern verurteilt war. Der Mathematiker Kurt Gödel (1906-1978) sollte schlussendlich zeigen, dass derartige Versuche der Formalisierung der Welt nicht möglich sind.

1847 führte der englische Mathematiker und Philosoph Georg Boole in seinem Buch The Mathematical Analysis of Logic [Boole, 1847] die sog. boolsche Algebra ein. Insbesondere die zweielementige boolsche Algebra mit den Elementen 0 und 1, welche Anwendung in der Aussagenlogik hat, sollte sich als Meilenstein der bis dato noch nicht existierenden Informatik herausstellen. Sie ist Teil jeder modernen Programmiersprache. Zusätzlich beruhen auf ihr alle (auch arithmetische) Operationen des digitalen Computers. Die boolsche Algebra definiert logische Operatoren wie AND \((\land)\), OR (\(\lor\)) und NOT \((\neg)\), die auf die Elemente 0 und 1 angewendet werden können wobei 0 als falsch und 1 als wahr interpretiert werden. Andere Operationen wie NAND (not AND), NOR (not OR), XOR (entweder oder) und NXOR (nicht entweder oder) können aus den Basisoperationen durch Kombination konstruiert werden.

Um 1930 beobachtete Claude Shannon, dass sich die Regeln der boolschen Algebra auf elektrische Schaltungen übertragen lassen. Seither stellen elektrische Schaltungen die physikalische Manifestation boolscher Operationen in fast allen digitalen Computern dar. Durch Logikgatter werden diese Operatoren in Computern realisiert und bilden die Basis jedweder Berechnung.

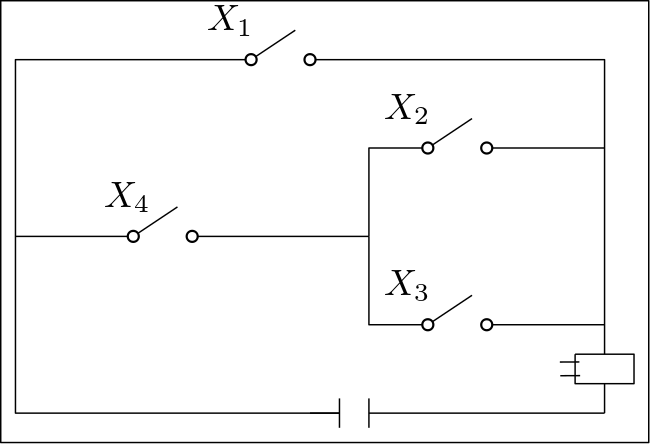
Abb. 3.4 Elektrischer Schaltkreis für den logischer Ausdruck \(X_1 \lor (X_4 \land (X_2 \lor X_3))\).

Wie die Aussagenlogik so verzichtet auch die boolsche Algebra auf einen Geltungsbereich der Variablen. Mit anderen Worten Sie kennt keine Quantoren \((\forall\), \(\exists)\). Auch kennt sie das Prinzip des Prädikats nicht, obwohl bereits Aristoteles Prädikate definierte.

In umgangssprachlicher Annäherung ist ein Prädikat eine Folge von Wörtern, die Leerstellen eröffnen; diese Folge wird zu einer wahren oder falschen Aussage, wenn in jede Leerstelle ein Eigenname eingesetzt wird. Beispielsweise ist: „… ist ein Mensch“ ein Prädikat. Ein mathematisches Prädikat ist eine Funktion die (bestimmten) mathematischen Objekten einen Wahrheitswert zuweist. Beispielsweise ist

\[P(x) = x \text{ ist eine gerade Zahl}\]

ein Prädikat, wobei beispielweise \(P(2) = \text{wahr}\) ergibt und \(P(3) = \text{falsch}\). Um Elementen aus Mengen auszuwählen gibt es die Quantoren. So lässt sich der Satz: „Für jede ungerade Zahl gibt es eine natürliche Zahl, mit der man diese multiplizieren kann, sodass das Ergebnis eine gerade Zahl ist“ wie folgt ausdrücken:

\[\forall n \in \mathbb{Z} \, \exists k \in \mathbb{N}: \neg P(n) \Rightarrow P(n \cdot k).\]

Diese Logik erster Ordnung oder auch Prädikatenlogik wurde insbesondere von Ludwig Gottlob Frege (1848-1925) in seinem Werk Begriffsschrift [Frege, 1879] entwickelt. Freges vorrangiges Ziel war der Logizismus, d.h. zu zeigen, dass die Mathematik als Teil der Logik auszuweisen ist. In anderen Worten wollte er alle mathematischen Sätze aus wenigen rein logischen Axiomen ableiten. Dieses Unterfangen war nur aussichtsreich, wenn ein Mittel zur Verfügung stand, mit dem sich die Lückenlosigkeit einer Schlusskette zweifelsfrei überprüfen ließ. Da sich die traditionelle Aristotelische Logik (Syllogistik) als unbrauchbar für diesen Zweck herausstellte, nahm sich Frege zunächst der Aufgabe an, eine neue, geeignetere Logik zu schaffen.

Abb. 3.5 Einflussreiche Logiker ihrer Zeit: Georg Boole, Gottlob Frege und Bertrand Russell, Quellen: 1, 2.

3.2.4. Zerstörte Träume und fruchtbare Theorien

Die Freges Prädikatenlogik wurde druch Bertrand Arthur William Rusell (1872-1970) und Alfred North Whitehead (1861-1947) weiterentwickelt. Sie machten die Logik zum Objekt wissenschaftlicher Forschung. Deren Logizismus und Formalismus führte zum sogenannten Grundlagenstreit der Mathematik in dem sich Formalismus und Intuitionismus, vertreten durch Luitzen Egbertus Jan Brouwer (1881-1966), gegenüber standen. Die Formalisten, insbesondere David Hilbert (1862-1943), wollten mathematische Grundsätze auf eine (bewiesenes) konsistente axiomatische Basis stellen. Die Intuitionisten glaubten, dass dies nicht möglich sei. Zudem zweifelten sie an der Gültigkeit des Satz vom ausgeschlossenen Dritten und des indirekten Beweises.

Hilbert schlug 1920 ein Forschungsprogramm vor das zum Ziel hatte, mit finiten Methoden die Widerspruchsfreiheit der Axiomensysteme der Mathematik nachzuweisen. Auch wenn sich das Hilbertprogramm in seinem ursprünglichen Anspruch als undurchführbar erwiesen hat, trug es dennoch entscheidend dazu bei, die Grundlagen und Grenzen mathematischer Erkenntnis zu klären. Das Programm fand breite Beachtung. Viele bekannte Logiker und Mathematiker beteiligten sich daran, unter anderem Paul Bernays (1888-1977), Wilhelm Ackermann (1896-1962), John von Neumann (1903-1957), Jacques Herbrand (1908-1931) und Kurt Gödel (1906-1978). Sie zeigten die Widerspruchsfreiheit und Vollständigkeit für zentrale Teilgebiete der Logik, nämlich für die klassische Aussagen- und Prädikatenlogik.

Aus dem Paradies, das Cantor uns geschaffen, soll uns niemand vertreiben können. – Hilbert

Hilbert, Russell und andere erzielten durch die Provokation der Intuitionisten weitreichende Erfolge. Russell und Whitehead gelang es in ihrem Werk Principia Mathematica [Russell and Whitehead, 1910] einige Gebiete der Mathematik auf ein solches Fundament zu stellen. Und David Hilbert und Wilhelm Ackermann (1892-1982) beschäftigten sich in Grundzüge der theoretischen Logik [Hilbert and Ackermann, 1928] unter anderem mit dem automatischen Prozessieren von logischen Berechnungen. Dabei formulierten sie das sog. Entscheidungsproblem formulierten. Es ist ein Problem, welche wie kein zweites die Logik und Informatik verbindet.

Das Entscheidungsproblem

Das Entscheidungsproblem verlangt nach der Beantwortung der Frage ob ein Algorithmus existiert, der für jedes Element einer vorgegebenen Menge beantworten kann, ob eine vorgegebene Eigenschaft zutrifft oder nicht?

Der österreichische Mathematiker Kurt Gödel (1906-1978) beantwortet die Frage mit einem nein und sowohl Alonzo Church (1903-1995) wie auch Alan Turing (1912-1954) veröffentlichen unabhängige Beiträge, die zeigen, dass das Entscheidungsproblem nicht zu lösen ist, sofern alles was grundsätzlich berechenbar ist, sich mit dem deckt, was Turing-berechenbar ist. Diese Annahme wird als Church-Turing-These bezeichnet. Trifft die These zu, kann alles was grundsätzlich berechenbar ist auch von einem Turing-vollständigen Computer (jedem modernen Computer) berechnet werden.

Über das Entscheidungsproblem konnte Turing die Fragestellung des sog. Halteproblem beantworten. Es wird demnach keinen Algorithmus geben können, der für jedes beliebige Programm mit beliebiger Eingabe festellen kann, ob dieses Programm jemals hält oder nicht. Für uns als Programmierer*innen bedeutet dies, dass wir selbst prüfen müssen ob unser Algorithmus das berechnet und vollzieht was vorgesehen ist. Es gibt keine Software, die uns für einen beliebigen Quellcode garantieren kann, dass wir keine Endlosschleife programmiert haben.

Abb. 3.6 Mathematiker Kurt Gödel, Alonzo Church und Alan Turing, Quellen: 1, 2, 3.

Was aus dem theoretischen Diskurs hervorging waren jedoch nicht nur zerstörte Träume, sondern auch neue fruchtbare Theorien, die das Fundament der Informatik und damit auch des künftigen Computational Thinkings prägen sollten. Alan Turing entwickelte mit seiner Turingmaschine ein sehr konkretes Modell für einen Computer, welcher im Stande war, all das zu berechnen, was heute moderne Computer berechnen können. Durch jenes Modell kann man noch heute prüfen ob konkrete Ingenieurskonstruktionen den Ansprüchen der Turing-Vollständigkeit genügen. Schon zu dieser Zeit belegt seine universellen Turingmaschine den fließenden Übergang zwischen Hard- und Software. Mit seiner Arbeit beeinflusste Turing imperative Programmiersprachen maßgeblich, wohingegen sein Doktorvater, Alonzo Church, mit dem Lambda-Kalkül funktionale Programmiersprachen ins Leben rufen sollte.

Aus der Frage der Berechenbarkeit folgte unweigerlich die Frage der Komplexität, also wie schwer ein Problem ist und wie dies zu messen ist. Lassen sich Probleme anhand ihrer Komplexität vergleichen? Was ist einfacher: ein Sudoku lösen oder Karten sortieren? Außerdem ergaben sich auch neue philosophische Fragen wie: Ist der menschliche Geist ein Informationsverarbeitungsprozess? Ist gar die Natur ein solcher Prozess oder kann sie zumindest als solcher modelliert werden? Ähnliche Fragen entstanden als die Mechanik ihren Siegeszug antrat. Zu dieser Zeit stellte man sich das menschliche Gehirn als eine Art Uhr vor. Inwieweit sich dieser Computationalismus bestätigt oder widerlegt wird bleibt noch immer abzuwarten.

Abb. 3.7 Eine konkrete Konstruktion einer Turingmaschine, Quelle.

3.2.5. Das maschinelle Lernen

Was aber heute in aller Munde ist, stammt aus dem Bereich des maschinellen Lernens. Schon in den 1940er Jahren wurde versucht die Informationsverarbeitung am Beispiel des menschlichen Gehirns zu modellieren. Dieser Ansatz wurde durch die Hirnforschung inspiriert. Die Idee war und ist es, eine riesige Anzahl an hochgradig vernetzten aber relativ simplen Neuronen durch Software zu simulieren. Die Idee der künstlichen neuronalen Netze (engl. artificial neuronal network (ANN)) war geboren.

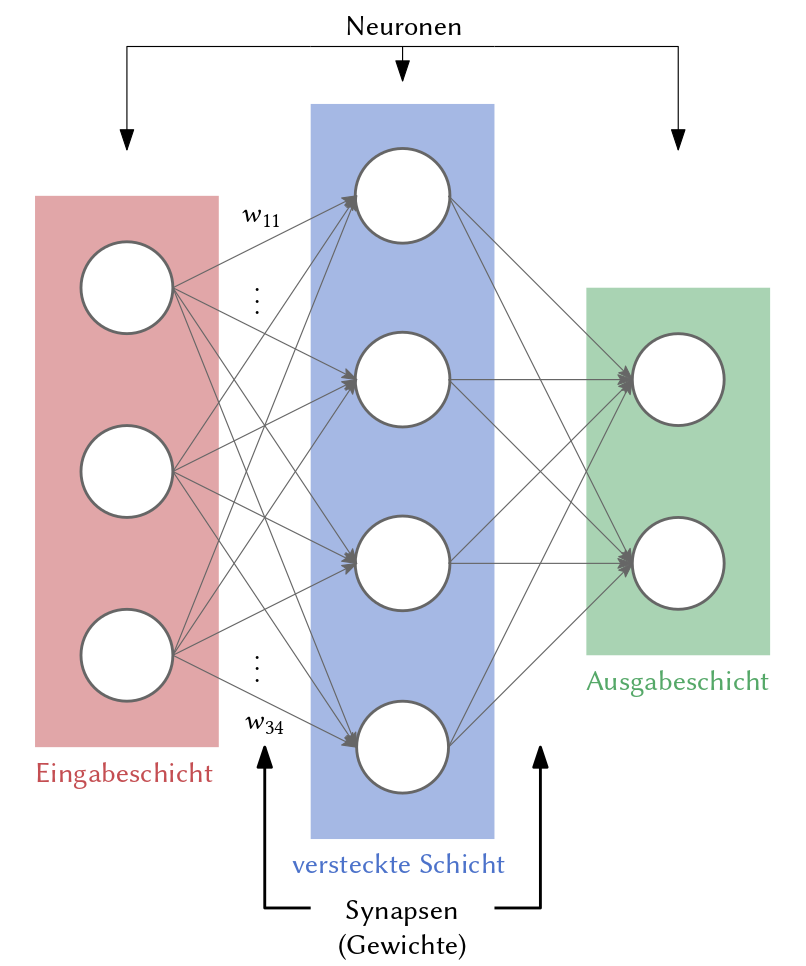
Abb. 3.8 Skizze eines künstliches neuronalen Netzes.

Um 1960 wurde eine wichtige Erweiterung der neuronalen Netze, die sog. tiefen neuronalen Netze (engl. deep neural networks (DNN)), vorgeschlagen. Anders als herkömmliche neuronale Netze (siehe Abbildung 3.8 ) bestehen diese aus mehrere versteckten Schichten. Zu jener Zeit fehlten allerdings die Daten und die Rechenleistung, um derartige DNNs praktisch nutzen zu können. Auch hatte men Schwierigkeiten die benötigten Gradienten im Zaum zu halten. Erst in den 80er Jahren wurden erste praktikable künstliche neuronalen Netze entwickelt [LeCun et al., 1989]. ANNs bilden eine Teilmenge der Algorithmen des maschinelles Lernen. Tom Mitchell definiert maschinelles Lernen wie folgt:

Ein Computerprogramm lernt von der Erfahrung \(E\) in Bezug auf eine Klasse von Aufgaben \(T\) und einer Bewertungsmetrik \(P\), wenn dessen Fähigkeit die Aufgaben \(T\) zu lösen, sich in Bezug auf die Bewertungsmetrik \(P\), mit der Erfahrung \(E\), verbessert. – Tom Mitchell, 1997

Der wesentliche Unterschied zwischen einem klassischen Algorithmus und dem maschinellen Lernen ist somit in seinen Augen, dass sich der Algorithmus anhand der Daten, die er verarbeitet, selbständig anpasst – er lernt von seinen Erfahrungen. Ein sehr einfaches Beispiel ist der sog. Spamfilter. Ein Spamfilter befolgt keine fest eingebrannten Regeln, sondern lernt was Spam und was kein Spam ist, indem wir E-Mails als Spam markieren. Er benötigt Trainingsdaten und kann dann neue Daten selbständig klassifizieren.

Insbesondere tiefe neuronalen Netze (DNNs) konnten erfolgreich für Aufgaben eingesetzt werden, die zuvor als unlösbar galten. Zu nennen ist die Sprach- (Microsoft 2011) und Bilderkennung [Cireşan et al., 2012, Krizhevsky et al., 2017].

Der Erfolg ist auf drei Faktoren zurückzuführen: Zu nennen ist die hohe Datenmenge. Facebook sammelt täglich etwa 350 Millionen Bilder und YouTube ca. 300 Stunden Videomaterial pro Minute. Durch die Integration der Technik in unser alltägliches Leben, bekannt unter dem Schlagwort Internet der Dinge (engl. Internet of Things (IoT)), können und werden weitere Daten von einem anderen Typ bzw. von einer anderen Qualität gesammelt.

Der zweite Faktor ist die hohe Rechenleistung, die uns in den letzten Jahren zur Verfügung stand. Sie erlaubt es uns die Algorithmen aus den 80er Jahren auf jene Daten loszulassen. Diese Algorithmen sind im Stande Strukturen in jenen Daten zu finden.

Der dritte wesentliche Faktor stellt die anfängliche Erfolgsgeschichte dar. Keiner wusste so recht, ob diese Netze tatsächlich nützlich sind. Die überraschend guten Resultate führten zu einer Flut an Entwicklungen neuer Algorithmen und Open-Source-Bibliotheken. Insbesondere das Python-Ökosystem wurde befüllt.

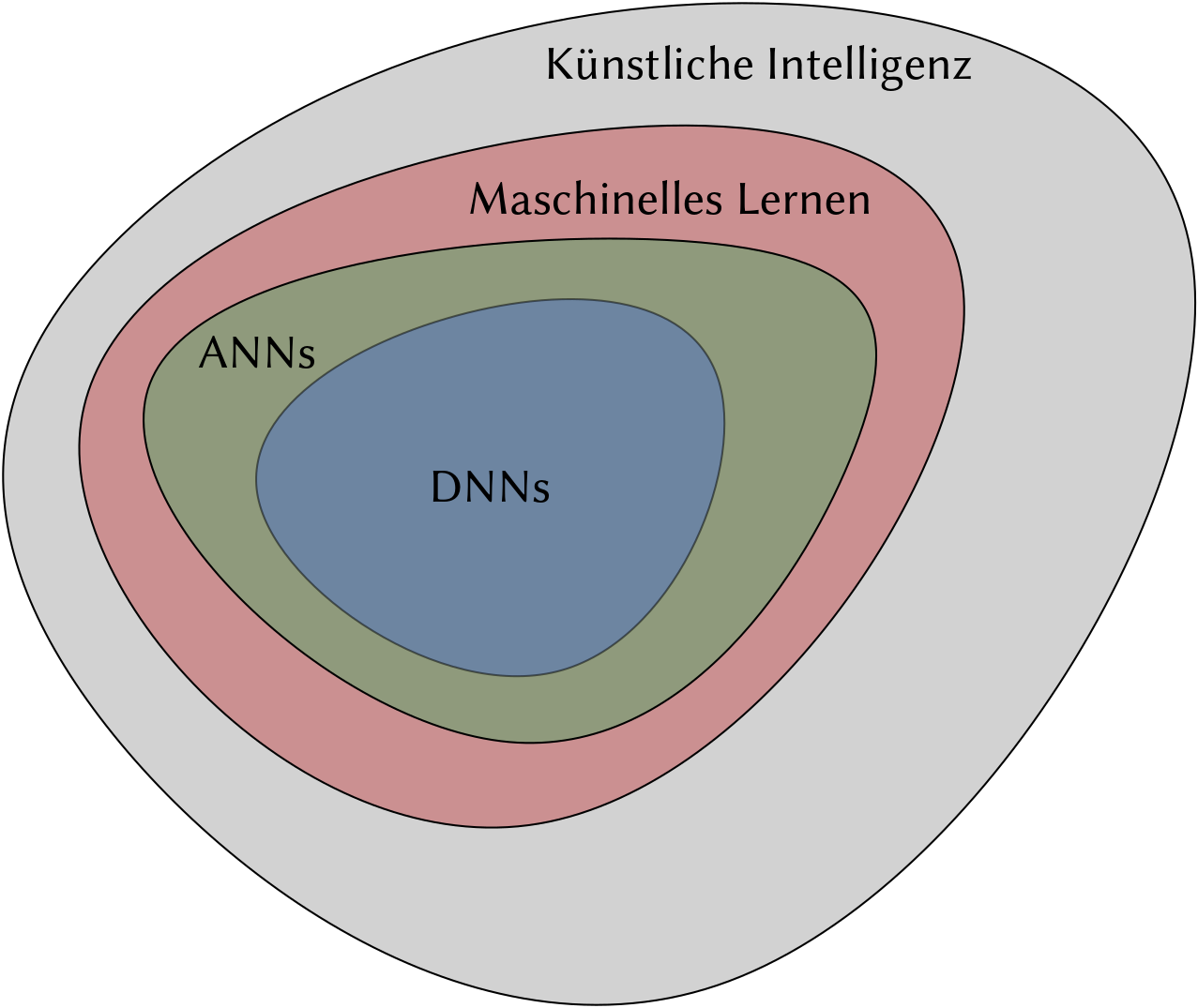
Das maschinelle Lernen ist wiederum eine Unterkategorie der künstlichen Intelligenz (KI) (engl. artificial intelligence (AI)). Der Begriff wurde 1956 von John McCarthy eingeführt.

[Es sei das Ziel von künstlicher Intelligenz], intelligentes menschliches Verhalten durch Computerprogramme (künstlich) nachzubilden. – John McCarthy

Die Themen KI im Allgemeinen und maschinelles Lernen im Besonderen werden uns auch in Zukunft noch beschäftigen. Die bisherigen Erfolge sind vielversprechend und möglicherweise können uns diese Algorithmen in vielen Bereichen eine echte Stütze sein. Dabei sollten wir einen gesunden Umgang mit KI-Systemen entwickeln. Fragen der Ethik, Ökologie und der sozialen Gerechtigkeit müssen in diesem Zuge ihren Platz im Diskurs finden. Das maschinelle Lernen wird sich auf all jene Bereiche ausbreiten für die wir große Datenmengen gesammelt haben oder sammeln können. Anbieter können so ihre Produkte optimieren—was auch immer das im Einzelnen bedeuten mag. KI kann uns möglicherweise helfen die Erderwärmung zu reduzieren, gleichzeitig benötigen diese daten- und energiehungrigen Algorithmen viele Ressourcen. Diese Spannung zwischen Nutzen und Kosten müssen wir beleuchten.

Daten sind heute ein echtes Wirtschaftsgut. Uns allen sollte bewusst sein, dass diese immense, oft undurchsichtige Datensammlung auch ihre Schattenseiten hat. Insbesondere wenn personenbezogene Daten gesammelt werden, müssen wir kritisch hinterfragen was mit diesen Daten gemacht wird und ob wir mit dieser Entwicklung einverstanden sind. Auch hängt die Qualität der Entscheidung eines lernenden Algorithmus von dessen Erfahrungen, d.h., den (Trainings-)Daten ab. Diskriminierungen, welche sich in den Daten finden, werden auch lernende Algorithmen durch die Reproduktion von Stereotypen übernehmen. Darüber hinaus muss in einer rechenzentrierten Gesellschaft beleuchtet und kritisch hinterfragt werden, in welcher Gewalt die nötigen Rechenressourcen liegen.