21. Sprechen in der Taucherglocke#

Lernziel

In diesem Abschnitt lernen Sie die Grundprinzipien der Informationsübertragung. Sie erlernen den Unterschied zwischen Information, Daten und Codierung und wie Kommunikation durch Einhaltung eines Protokolls möglich wird.

Wir entwerfen und verbessern Algorithmen zur Kommunikation und diskutieren, wie sich Algorithmen vergleichen lassen.

In dieser Übung beschäftigen wir uns mit der linearen und binären Suche, Codierungsbäumen, künstlicher Intelligenz und welche Fragen zur Technik wir uns Entwickler*innen möglicherweise widmen sollten.

Beim sogenannten Locked-in-Syndrom ist man infolge eines Schlaganfalls vollständig gelähmt. Man kann zwar weiterhin ganz normal denken, sehen und hören, kann aber oft lediglich die Augenlider bewegen (und manchmal auch das nicht). Oft sind die Heilmöglichkeiten sehr begrenzt und es bleibt den Mediziner*innen nur die Möglichkeit den Patient*innen das Leben so angenehm wie möglich zu gestalten.

Sich mitzuteilen, sich zu verständigen, sich auszudrücken ist ein Grundbedürfnis eines jeden Menschen. Eingeschlossen in unseren Körpern gelangen Ideen und Gefühle über Körperregungen in die Welt und deren Reaktion wieder zurück zu uns. Mit 43 Jahren erlitt der französische Schriftsteller Jean-Dominique Bauby im Dezember 1995 einen schweren Schlaganfall. Als er nach zwanzig Tagen im Krankenhaus wieder aufwachte, war er buchstäblich sprachlos. Er konnte nur noch mit seinem linken Augenlid blinzeln. Der Körper versagte ihm nahezu alle Möglichkeiten der Verständigung und doch gelang es Dominique, über seine Erlebnisse in der geistigen Isolation, ein ganzes Buch zu schreiben. Wie war dies möglich?

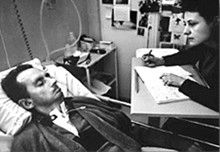
../../_images/jean-dominique-bauby.jpeg

Abb. 21.1 Jean-Dominique Bauby (links) diktiert sein Buch Claude Mendibil (rechts), Quelle.#

In seinem äußerst bewegenden Buch Schmetterling und Taucherglocke beschreibt er wie es ihm gelungen ist mit seinen Ärzten, Pflegern, Freunden und seiner Familie zu kommunizieren und wie frustrierend es gewesen ist, wenn seine Kommunikationspartner von den Regeln abwichen und so die Kommunikation abbrach. Er liefert uns tiefe Einblicke darüber, wie wichtig Verständigung für den Menschen ist und wie sehr wir einander brauchen um uns selbst nicht zu verlieren.

Während Dominique sein Buch schrieb entwickelte er einen Algorithmus um die Kommunikation zu beschleunigen. Ohne es zu wissen bediente er sich des Computational Thinkings. Im alter von 44 Jahren, zwei Tage nach der Veröffentlichung seines Buchs, verstarb Dominique an einer Lungenentzündung.

In diesem Abschnitt werden wir uns ansehen wie er die Kommunikation aufbaute und wesentlich verbesserte. Wir werden jedoch noch einen Schritt weiter gehen und eine weitere Verbesserung entwickeln. Dabei werden wir uns selbst in Dominique und seinen Helfer*innen hineinversetzen, um seine Techniken frisch zu entdecken und zu praktizieren.

21.1. Blinzelnd sprechen#

Dominique war im Stande zu blinzeln. Alle andere Art der Bewegung wurde ihm verwehrt. Er konnte keinen Laut von sich geben, den Finger nicht rühren und die Zehen nicht zucken lassen. Er konnte jedoch Anweisungen verstehen. Seine kognitive Wahrnehmung blieb uneingeschränkt. Stellen Sie sich nun vor Sie sind der Artzt oder die Ärtztin von Dominique.

Exercise 21.1 (Blinzeln des Alphabets)

Überlegen Sie sich einen Algorithmus, durch den Sie mit Dominique kommunizieren können.

Bereits jetzt sind Sie als Informatiker*in aktiv! Bevor wir überhaupt über den Computer auch nur nachgedacht haben, ist es uns gelungen einen Algorithmus zu entwickeln durch den wir Informationen (das Blinzeln) verarbeiten können. Wir haben ein Herzstück des Computational Thinkings betrieben: das algorithmische Denken.

Ähnlich wie in der Astrologie, in der das Teleskop ein Werkzeug und nicht der wesentliche Forschungsbestandteil ist, so ist die Informatik nicht die Wissenschaft des Computers sondern der Informationsdarstellung, Verarbeitung und Speicherung.

Das tolle an einem Algorithmus ist, dass wir seine einzelnen Anweisungen abarbeiten können, ohne zu verstehen was wir eigentlich im Großen und Ganzen genau tun. Solange die Ausführenden, in diesem Fall Sie und Dominique, die einzelnen Anweisungen verstehen, können Sie den Algorithmus ausführen. Wir könnten eine Tabelle schreiben in der für jede Anzahl an Augenblinzeln der entsprechende Buchstabe steht, sodass Dominique nur richtig blinzeln muss und wir richtig zählen müssen.

Durch stupides befolgen der Anweisungen entstehen erst wenige Buchstaben, dann Sätze, irgendwann Abschnitte, kleine Geschichten und schließlich ein ganzes Buch, was als Gesamtwerk vielschichtige Bedeutungen in sich trägt. Das Buch als Folge von sich bewegenden Augenlidern und Pausen oder als Text enthält die gleiche Information jedoch unterschiedlich repräsentiert.

Beim Zählen der Auf- und Abwärtsbewegung der Augenlider kommt der (digitale) Computer ins Spiel, denn anders als wir Menschen, führen Computer solche Aufgaben immer korrekt aus. Sie verzählen sich niemals! Früher waren menschliche Computer ebenfalls darauf trainiert bei sich wiederholenden Aufgaben möglichst wenig Fehler zu machen. Passiert sind diese verständlicherweise dennoch immer wieder.

Testen Sie den Algorithmus mit ihren Kommiliton*innen.

Exercise 21.2 (Name blinzeln)

Verwenden Sie den einfachen Blinzelalgorithmus aus obiger Lösung und diktieren Sie ihrem Nachbarn ihren Namen. Was fällt Ihnen auf?

21.2. Interaktives Blinzeln#

Besitzen Sie einen Namen dessen Buchstaben weit hinten im Alphabet zu finden sind, werden Sie vermutlich für das Diktieren viel Zeit gebraucht haben. Insgesamt, ist dieses Schema doch recht umständlich. Sie müssen im schlimmsten Fall für nur einen Buchstaben \(26\) Mal blinzeln und ihr Gegenüber ist die meiste Zeit mit dem Zählen beschäftigt. Und möchten Sie Leerzeichen oder gar Sonderzeichen einführen, hat Ihre Menge, welche sie codieren wollen, bereits mehr als \(26\) Elemente.

Nachdem Dominique, wenn auch umständlich, kommunizieren konnte war es ihm möglich einen verbesserten Algorithmus seinem Gegenüber mitzuteilen. Wenn Sie obigen Algorithmus angewendet haben, kommen Sie vielleicht selbst auf seine Verbesserung.

Exercise 21.3 (Interaktives Blinzeln)

Entwerfen Sie einen effizienteren Algorithmus der Kommunikation und testen Sie diesen.

Tipp: Die oder der zuvor Zählende stellt eine Frage und Dominique antwortet darauf.

Was wir bis jetzt noch nicht besprochen haben ist die Tatsache, dass unsere entwickelten Algorithmen eigentlich aus zwei Teilen bestehen. Wir haben den- oder diejenige die blinzelt und die- oder denjenigen der zählt oder aber die Buchstaben und Sonderzeichen ausspricht. Die Reihenfolge in der diese beiden Parteien Informationen austauschen strukturiert die Information.

Möglicherweise passieren Fehler, zum Beispiel könnte es passieren, dass wir zu schnell sprechen und wir den falschen Buchstaben notieren. Es wäre sinnvoll die Möglichkeit zu haben einen Buchstaben zurückzunehmen bzw. eine Aktion rückgängig zu machen. Sie werden beobachten, dass wann immer Menschen Teil der Informationsverarbeitung sind, es immer irgendeine Möglichkeit gibt etwas rückgängig zu machen. Wir machen einfach gerne Fehler. In unserem Fall könnten wir uns darauf einigen, dass zweimal schnell blinzeln bedeutet, dass das letzte Zeichen zurückgenommen wird.

Im Grunde schicken sich die beiden Teilnehmer*innen der Kommunikation bestimmte Informationen hin und her. Der oder die Sprecher*in beginnt mit A und Dominique blinzelt oder wartet. Der oder die Sprecher*in wartet eine kurze Weile und falls kein Blinzeln kommt spricht sie/er das B aus. Notiert sie/er versehentlich den falschen Buchstaben, so kann Dominique mit einem zweifachen Binzeln dies korrigieren.

Einen solchen Algorithmus, der eine Menge von Regeln für den Informationsaustausch bestimmter Informationen beschreibt, nennen Informatiker Kommunikationsprotokoll.

Kommunikationsprotokoll

Ein Kommunikationsprotokoll ist eine Vereinbarung zum Austausch von Informationen. Sie besteht aus einem Satz von Regeln und Formaten (Syntax), die das Kommunikationsverhalten der kommunizierenden Instanzen in den Computern bestimmen (Semantik).

Wenn Sie mit ihrem Computer oder ihrem Handy über das Netzwerk kommunizieren, dann wird dieser Informationsaustausch ebenfalls über ein (sehr viel komplexeres) Protokoll geregelt. Im Wesentlichen unterscheiden sich diese Protokolle nicht von Protokollen die Sie bereits aus Ihrem Alltag kennen. Senden Sie zum Beispiel einen Brief, so setzen alle beteiligten Parteien ein bestimmtes Protokoll um. Manche Protokolle verwenden wir unbewusst, beispielsweise, wenn wir in einer Gruppe kommunizieren, dann befolgen wir bestimmte Regeln bestehend aus Sprechen, Zuhören und Warten. Folgen Teilnehmer dem Protokoll nicht, so wird der Informationsaustausch erschwert oder er kommt ganz zum erliegen. So berichtet Dominique von seinen Frustrationen, wenn seine Gesprächspartner sich nicht an das Protokoll gehalten haben.

Denken in Algorithmen ist eine mächtige Art zu denken. Sie gelangen so zu Lösungsstrategien die nicht nur für ein spezielles Problem eine Lösung berechnen, sondern für eine ganze, gewöhnlicherweise unendliche Anzahl an Problemen Lösungen berechnen können. Mit dem beschriebenen Algorithmus können Sie all das kommunizieren, was sie auch niederschreiben könnten. Es ist eben nicht nur eine Möglichkeit ein bestimmtes Wort oder einen bestimmten Satz wiederzugeben!

Dominique verwendete seinen Algorithmus andauernd und wurde zum Experten. Ihm viel dadurch eine weitere recht einfache Verbesserung auf. Seine Beobachtung hat etwas mit der Verteilung bzw. Häufigkeit der Buchstaben in bestimmten Sprachen zu tun und wurde bei der Entschlüsselung von verschlüsselten Nachrichten eingesetzt. Wenn Sie unseren aktuellen Algorithmus länger verwenden kommen Sie vielleicht auf Dominique’s Verbesserung?

Exercise 21.4 (Häufigkeit der Buchstaben)

Verbessern Sie Ihren Algorithmus indem Sie die Reihenfolge der Buchstaben des Sprechers optimieren. Probieren Sie den neuen Algorithmus aus.

Mit den fünf häufigsten Buchstaben haben wir ca. \(50\,\%\) aller Buchstaben in deutschen Texten abgedeckt. Dadurch kann sich der Sprecher deutlich kürzer fassen. Wenn Sie sich nicht anders ausdrücken können, spart das viele viele Stunden an Zeit.

21.3. Blinzeln mit der KI#

Was wir bis jetzt noch gar nicht in Betracht gezogen haben ist, dass Dominique mit einem intelligenten Wesen kommuniziert. In diesem Falle ist diese Intelligenz nicht künstlich. Die nächste Verbesserung könnten wir jedoch als künstliche Intelligenz umsetzen.

Sie werden als Sprecher vielleicht bemerkt haben, dass Sie oftmals erahnen welches Wort gemeint ist. Notieren Sie zum Beispiel, Algo dann handelt es sich wahrscheinlich um das Wort Algorithmus. Wörter haben Struktur und sind keine rein zufällig aneinandergereihten Buchstaben. Diese Struktur können wir nutzen, aber wie?

Exercise 21.5 (Vervollständigung)

Verbessern Sie Ihren Algorithmus durch eine Auto-Vervollständigung.

Tipp: Denken Sie an die Auto-Vervollständigung ihres Handys.

Im Falle der Sprecher*innen und Dominique müssen die Sprecher*innen abschätzen, wann es sich lohnt ein Wort vorzuschlagen. Hierbei aktiviert die Person ihre Mustererkennung. Sie wird, je länger sie mit Dominique kommuniziert, sehr wahrscheinlich immer besser. Das liegt nicht nur daran, dass sie im Wörterraten an sich besser wird, sondern auch daran, dass sie Dominique’s Wortschatz aufnimmt. In der Sprache des maschinellen Lernens sagt man: Die Sprecher*innen verbessern ihr Modell von Dominique’s Wortschatz und bevorzugter Satzstruktur.

Jeder Mensch verwendet Wörter in einer anderen Häufigkeit und so lernt der oder die Sprecher*in (sofern es immer die gleiche Person ist), wie Dominique spricht. Durch Daten (den Wörtern) und deren Struktur (Kombination, Reihenfolge, Sätze bzw. Grammatik) lernen die Sprecher*innen genau jene Struktur bzw. Häufigkeiten. Kommen neue Daten bei ihnen an, können sie die gelernte Struktur nutzen. Algorithmen die derartige Lernverfahren realisieren stammen aus dem Bereich der künstlichen Intelligenz (KI).

Dominique hatte nicht nur eine(n) Sprecher*in. Ärtz*innen und auch Pfleger*innen wechselten durch und hin und wieder kamen neue Sprecher*innen hinzu. Wie könnten wir das gelernte Wissen der Sprecher*innen weitergeben?

Exercise 21.6 (Maschinelles Lernen)

Nehmen Sie an, dass die Sprecher*innen immer wieder durchwechseln bzw. ihr gelerntes Wissen verlieren. Beschreiben Sie wie man die Häufigkeit der von Dominique verwendeten Wörter festhalten und weitergeben kann.

Dictionary wdh. (Python)

Ein Python Dictionary ist eine ungeordnete Sammlung von Daten. Jeder Datenpunkt bzw. Wert value benötigt einen eindeutigen Schlüssel key und kann über diesen Angesprochen werden.

Beispiel: (Schlüssel ist eine Zeichenkette, Wert ist eine Ganzzahl)

word_frequency = {'hallo': 100, 'hilfe': 50, 'nein': 300, 'ja': 210}
word_frequency['hallo']

Durch ein Python Dictionary können wir eine solche Worttabelle in der Programmiersprache Python realisieren. Diese Art von Datentyp finden Sie in allen Programmiersprachen, oft unter einem anderen Namen, z.B. Map oder HashMap.

Anders als bei einer Tabelle, welche wir später noch kennenlernen, sind die Schlüssel-Wert-Paare ungeordnet. Einer Tabelle könnte zudem zweimal den gleichen Schlüssel enthalten, was in einem Dictionary nicht möglich ist. Durch die Eindeutigkeit des Schlüssels ist der Zugriff auf den Wert durch den Schlüssel sehr schnell.

Denken Sie gerne in mathematischen Objekten dann ist ein Dictionary \(D : K \rightarrow V\) nichts anderes als eine Funktion, wobei sowohl der Definitionsbereich \(K\) als auch der Wertebereich \(V\) endlich sind. \(K\) enthält die Schlüssel und \(V\) die Werte. Wir werden im Abschnitt Hashing unser eigenes Dictionary konstruieren und näher auf das Prinzip sogenannter Hashfunktionen, durch die wir mit einem gegebenen Schlüssel zu seinem Wert gelangen, eingehen.

Exercise 21.7 (Maschinelles Lernen)

Schreiben Sie einen Programmiercode der Ihnen für ein bestimmtes Wort, sagen wir word, die Häufigkeit von word ein einem Dictionary um eins erhöht. Gehen Sie davon aus, dass Sie nicht wissen wie das derzeitige Dictionary word_frequency aussieht. Geben Sie ihr Dictionary aus und führen Sie den Code mehrfach aus. Was beobachten Sie?

word_frequency = {...}
word = 'danke'
...
word_frequency

word_frequency = {'hallo': 100, 'hilfe': 50, 'nein': 300, 'ja': 210}
word = 'danke'

if word in word_frequency:
    word_frequency[word] += 1
else:
    word_frequency[word] = 1

word_frequency

{'hallo': 100, 'hilfe': 50, 'nein': 300, 'ja': 210, 'danke': 1}

Kommen wir zurück zu Dominique und unserer Tabelle. Die Tabelle wird sich sehr schnell füllen und dies per Hand festzuhalten wird schwierig. Außerdem müssten wir unsere Tabelle hin und wieder nach der Häufigkeit der Wörter sortieren, ansonsten suchen wir ewig nach den häufigsten Wörtern.

Exercise 21.8 (Temporäres Lernen)

Überlegen Sie sich eine praktikable Möglichkeit wie wir die Lernmethode sinnvoll handschriftlich verwenden können.

Wie würden wir die \(n\) häufigsten Wörter in absteigender Reihenfolge aus unserem Python Dictionary extrahieren? Können Sie hierfür eventuell die gleichen Algorithmen verwenden wie in Karten sortieren in Python?

Exercise 21.9 (Temporäres Lernen mit dem Dictionary)

Schreiben Sie eine Programmcode der Ihnen die n häufigsten Wörter in sortierter absteigender Reihenfolge aus dem Dictionary word_frequency extrahiert.

Tipp: Bauen Sie eine Liste die alle Schlüssel enthält und sortieren Sie diese anhand des Dictionarys. Sie können den Code aus Karten sortieren in Python verwenden.

########### Diesen Code haben wir einfach kopiert ###########
def find_smallest_index(hand, is_smaller):
    index = 0                                
    for i in range(len(hand)):               
        if is_smaller(hand[i], hand[index]): 
            index = i
    return index

def remove_smallest_card(hand, is_smaller):
    i = find_smallest_index(hand, is_smaller)
    card = hand[i]
    del hand[i]
    return card

def stack_sort(hand, is_smaller):
    stack = [];                          
    while len(hand) > 0:                 
        card = remove_smallest_card(hand, is_smaller)
        stack.append(card)
    return stack

def index_of(card):
    cards = get_cards()
    for index in range(len(cards)):
        if cards[index] == card:
            return index
##################################################################

n = 10
keys = []
# 1. baue Liste aus keys
for key in word_frequency:
    keys.append(key)

# 2. sortiere keys wobei der Vergleichsoperator gleich der Vergleich der Werte ist.
keys = stack_sort(keys, lambda a, b: word_frequency[a] > word_frequency[b])

# 3. gebe die n häufigsten keys/Wörter aus
keys[0:n]

['nein', 'ja', 'hallo', 'hilfe', 'danke']

Im obigen Code verwenden wir eine sog. anonyme Funktion, welche in Python mit dem lambda-Konstrukt realisiert werden können.

21.4. Wie gut ist mein Algorithmus?#

Wenn Sie die bisher entwickelten Algorithmen ohne technischen Hilfsmittel selbst angewendet haben, werden Sie feststellen, dass wir immer und immer schneller geworden sind, oder? Haben wir mehrere Algorithmen für den Informationsaustausch zwischen Sprecher*in und Dominique entwickelt, stellt sich die Frage, welche der beste Algorithmus ist. Mit besser meinen Informatiker*innen meistens schneller, doch gibt es auch andere Kriterien, zum Beispiel, die Energieeffizienz, Parallelisierbarkeit, Verständlichkeit oder auch Ästhetik.

Gehen wir also zurück in die Zeit von Dominique. Lassen Sie uns die beiden interaktiven Algorithmen vergleichen. Wir haben den einfachen interaktive Algorithmus bei dem das Alphabet von vorne nach hinten durchgesprochen wird und den verbesserte interaktive Algorithmus bei dem die Buchstaben in absteigender Häufigkeit ausgesprochen werden.

21.4.1. Laufzeitmessung#

Interessieren wir uns für den schnellsten Algorithmus, brauchen wir erst einmal ein geeignetes Maß mit dem wir die Berechnungszeit messen können. Eine erste Idee ist es einfach mit einer Stoppuhr die tatsächlich benötigte Zeit zu messen. Wir nehmen einen Text und messen für beide Algorithmen die Zeit die es braucht diesen auszudrücken.

Tatsächlich werden solche Messungen durchgeführt insbesondere dann, wenn es nicht mehr ersichtlich ist, wie viele Anweisungen genau während des Ablaufs des Algorithmus durchgeführt werden. Hin und wieder werden unterschiedliche Anweisungen ausgeführt und jede Anweisung dauert unterschiedlich lange. Unterschiedliche Algorithmen verwenden unterschiedliche Anweisungen unterschiedlich oft und diese können auf unterschiedlicher Hardware unterschiedlich schnell abgearbeitet werden. Insofern bietet die Messung der Laufzeit immerhin einen kleinen Einblick.

Doch müssen wir aufpassen! Was ist wenn Dominique bei jedem Versuch immer schneller blinzelt weil er geübt ist? Oder vielleicht kommt ihm bei einem Versuch ein wenig Staub in die Augen und er ist besonders langsam. Vielleicht wird er nach ein paar wenigen Durchläufen müde und dadurch langsamer oder der bzw. die Sprecherin wird unkonzentriert. Diese Veränderung der Laufzeit hat nichts mit dem Algorithmus zu tun sondern mit den ausführenden Einheiten (den Computern).

Exercise 21.10 (Laufzeitmessung)

Wie könnten Sie die Zeitmessung der Algorithmen möglichst fair gestalten?

Nehmen wir nur einen (Test-)Text zur Analyse unserer Laufzeit, wissen wir lediglich wie der Vergleich für diesen einen Text ausfällt. Besser wäre es die Laufzeitmessung mit vielen verschiedenen Texten durchzuführen. Doch irgendwann wird Dominique müde werden und wir müssen an einem anderen Tag weiter machen.

Solche Laufzeitmessungen sind wichtig besonders wenn die theoretische Komplexität zweier zu vergleichender Algorithmen identisch ist. Was das bedeutet dazu kommen wir gleich. Doch mit welchen Daten und wie oft und unter welchen Voraussetzungen wir die Algorithmen ausführen, ist an und für sich ein schwieriger Bereich der Informatik. Häufig kommt es darauf an wie gut die gewählten Testdaten sind (z.B. ausgewogene Texte). Je nach Anwendungsbereich kann ein Algorithmus gute oder eher schlechte Laufzeiten haben.

Neben diesen experimentellen Ansätzen können wir aber auch einen anderen Pfad einschlagen, indem wir unser abstraktes Denken aktivieren. Gemeint ist der analytische Pfad.

21.4.2. Komplexitätsanalyse#

Anstatt in Zeit, denken wir bei der Komplexitätsanalyse in Aufwand. Und anstatt mit der Stoppuhr die Zeit zu messen, zählen wir den Aufwand bzw. schätzen diesen ab.

Da Dominique ohnehin nur blinzeln kann, können wir einfach zählen wie oft er blinzelt. Dabei gehen wir davon aus, dass jedes Blinzeln den gleichen Aufwand hat. Das heißt jedes Blinzeln dauert in etwa (aber nicht unbedingt genau) gleich lange. Ebenso behaupten wir, dass das Aussprechen eines Buchstabens immer in etwa gleich lange dauert.

In der Komplexitätsbetrachtung bedeutet in etwa gleich lang, dass es eine Konstante \(c\) gibt, sodass jede Ausführung der betrachteten Anweisung (z.B. Blinzeln) nicht länger als \(c\)-mal so lange dauert wie die schnellste Ausführung.

Das klingt natürlich absolut unbrauchbar, denn wir können \(c\) beliebig groß wählen. Wenn \(c\) zum Beispiel gleich \(1000\) ist, wie kann man dann noch von in etwa gleich lange sprechen? Nun den Theoretiker*innen ist nur wichtig, dass \(c\) nicht von der Eingabe des Algorithmus abhängt. In unserem Fall heißt das, dass \(c\) nicht von der Länge und Art des Textes abhängt, den Dominique uns mitteilen will.

Denken Sie an eine komplizierte Aufgabe, wie das Sortieren! Wenn das Sortieren von Karten in etwa so lange dauern würde wie einmal blinzeln, dann müsste es ein solches \(c\) geben und egal wie viele Karten wir auch sortieren, der Algorithmus würde niemals länger brauchen als \(c\)-mal die Zeit des Blinzeln. Glauben Sie, dass das so ist? Ist ein Algorithmus hingegen echt langsamer als ein anderer (im Sinne der Zeitkomplexität), dann wird ihn keine technische Verbesserung an den echt schnelleren Algorithmus heranbringen. Ist die Eingabe bzw. das Problem groß genug, wird der echt schnellere Algorithmus auch in Zukunft schneller sein.

Haben Sie keine Angst, falls sie das noch nicht im Detail durchdringen. Wir möchten das Thema hier nur anreißen und werden das Konzept der Komplexität eines Algorithmus noch genauer durchleuchten.

Exercise 21.11 (Blinzelgeschwindigkeit)

Weshalb könnte die Annahme, dass jedes Blinzeln gleich lange dauert falsch sein?

Aber nun erst einmal genug von der theoretischen Komplexität, diese betrachten wir näher im Abschnitt Komplexität.

Lassen Sie uns die beiden interaktiven Algorithmen vergleichen. Einmal Sprechen wir das Alphabet von vorne nach hinten durch und warten auf ein blinzeln von Dominik und einmal Sprechen wir die Buchstaben in absteigender Häufigkeit durch und warten ebenfalls. Für jeden Buchstaben muss Dominique also einmal blinzeln und der Sprecher muss unterschiedlich viele Buchstaben nennen. Das Blinzeln und das Aussprechen eines Buchstabens können wir als jeweils eine Anweisung verstehen die einen bestimmten Aufwand hat. Da Dominique für jeden Algorithmus pro Buchstabe einmal blinzelt, können wir den Aufwand für das Blinzeln als identisch annehmen. Bleibt die Frage nach dem Aufwand für das Sprechen der Buchstaben.

Betrachten wir den einfachen Algorithmus bei dem der Sprecher das Alphabet von vorne bis hinten durchspricht und ignorieren wir alle Sonderzeichen. Wir könnten uns nun nach dem schlimmsten Fall fragen. Wenn uns Dominique lauter Z mitteilen möchte dann würde der Sprecher für jedes Z \(26\) ausgesprochene Buchstaben brauchen! Um ein Buch mit dem einfachen Algorithmus zu schreiben bräuchten wir also im schlimmsten Fall \(26 \cdot n\) ausgesprochene Buchstaben wobei \(n\) die Anzahl der Buchstaben in dem Buch ist. Im besten Fall bräuchten wir \(n\) (lauter As). Wie würde es aber im Durchschnitt aussehen? Nehmen wir für einen kurzen Moment an Dominique würde deutsch sprechen und er würde Buchstaben nach ihrer Häufigkeit verwenden.

Exercise 21.12 (Durchschnittlicher Aufwand)

Schreiben Sie ein kleines Programm was Ihnen den durchschnittlichen Aufwand anhand der Häufigkeit berechnet. Nehmen Sie an dass Dominique anstatt ß ein S schreiben würde. Sie können, wenn sie wollen, folgendes Dictionary der Häufigkeiten verwenden:

char_frequency = {'E': 0.1740, 'N': 0.0978, 'I': 0.0755, 
                  'S': 0.0758, 'R': 0.0700, 'A': 0.0651, 
                  'T': 0.0615, 'D': 0.0508, 'H': 0.0476,
                  'U': 0.0435, 'L': 0.0344, 'C': 0.0306,
                  'G': 0.0301, 'M': 0.0253, 'O': 0.0251,
                  'B': 0.0189, 'W': 0.0189, 'F': 0.0166,
                  'K': 0.0121, 'Z': 0.0113, 'P': 0.0079,
                  'V': 0.0067, 'J': 0.0027, 'Y': 0.0004,
                  'X': 0.0003, 'Q': 0.0002}

Tipp (für die Schreibfaulen): In Python können Sie Zeichenketten alphabetisch-lexikographisch vergleichen, z.B., resultiert 'A' < 'B' in True.

char_frequency = {'E': 0.1740, 'N': 0.0978, 'I': 0.0755, 
                  'S': 0.0758, 'R': 0.0700, 'A': 0.0651, 
                  'T': 0.0615, 'D': 0.0508, 'H': 0.0476,
                  'U': 0.0435, 'L': 0.0344, 'C': 0.0306,
                  'G': 0.0301, 'M': 0.0253, 'O': 0.0251,
                  'B': 0.0189, 'W': 0.0189, 'F': 0.0166,
                  'K': 0.0121, 'Z': 0.0113, 'P': 0.0079,
                  'V': 0.0067, 'J': 0.0027, 'Y': 0.0004,
                  'X': 0.0003, 'Q': 0.0002}
chars = list(char_frequency.keys()) # kürzer als Schleife
chars = stack_sort(chars, lambda a, b: a < b)

avg_effort = 0.0
for i in range(len(chars)):
    avg_effort += (i+1) * char_frequency[chars[i]]
avg_effort

11.1526

avg_effort (11.1526) ist der durchschnittliche Aufwand, d.h., die durchschnittlich auszusprechenden Buchstaben je geschriebenem Buchstaben. Interpretieren wir die Häufigkeit als Wahrscheinlichkeit ist es der Erwartungswert der auszusprechenden Buchstaben je geschriebenem Buchstaben. Lassen Sie uns das noch mit dem Aufwand der verbesserten Variante vergleichen, der in der wir die Buchstaben in der Reihenfolge ihrer Häufigkeit aufsagen.

Exercise 21.13 (Durchschnittlicher Aufwand für verbesserte Variante)

Schreiben Sie ein kleines Programm was Ihnen den durchschnittlichen Aufwand für die verbesserte Variante anhand der Häufigkeit berechnet. In dieser Variante beginnt der Sprecher mit dem häufigsten Buchstaben und folgt diesem Schema in absteigender Reihenfolge.

chars = list(char_frequency.keys()) # kürzer als Schleife
chars = stack_sort(chars, lambda a, b: char_frequency[a] > char_frequency[b])

avg_effort = 0.0
for i in range(len(chars)):
    avg_effort += (i+1) * char_frequency[chars[i]]
avg_effort

6.9836

Diesmal liegt der durchschnittliche Aufwand avg_effort bei 6.9836, d.h., die verbesserte Variante ist unter unserem Maß fast doppelt so schnell. Glücklicherweise sind die Buchstaben, die wir selten verwenden tendenziell auch hinten im Alphabet angesiedelt. Können Sie bestimmen welcher Buchstabe, bezüglich unseres Maß am schlechtesten im Alphabet positioniert ist?

Exercise 21.14 (Schlechtester Buchstabe im Alphabet)

Schreiben Sie ein kleines Programm was Ihnen den am schlechtest positionierten Buchstaben berechnet.

Tipp Nehmen Sie als Grundlage folgende Liste alphabet, welche alle Buchstaben in der richtigen Reihenfolge enthält.

alphabet = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J',
            'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T',
            'U', 'V', 'W', 'X', 'Y', 'Z'] 

chars_freq = list(char_frequency.keys())
chars_freq = stack_sort(chars_freq, lambda a, b: char_frequency[a] > char_frequency[b])

alphabet = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J',
            'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T',
            'U', 'V', 'W', 'X', 'Y', 'Z'] 

chars_diff = []

for i in range(len(alphabet)):
    char_alph = alphabet[i]
    for j in range(len(chars_freq)):
        char_freq = chars_freq[j]
        if char_alph == char_freq:
            chars_diff.append((char_alph, i-j))

chars_diff = stack_sort(chars_diff, lambda a, b: abs(a[1]) > abs(b[1]))
chars_diff

[('S', 16),
 ('B', -14),
 ('J', -13),
 ('R', 13),
 ('T', 13),
 ('F', -12),
 ('N', 12),
 ('U', 11),
 ('C', -9),
 ('Q', -9),
 ('K', -8),
 ('G', -6),
 ('W', 6),
 ('Z', 6),
 ('A', -5),
 ('I', 5),
 ('P', -5),
 ('D', -4),
 ('E', 4),
 ('H', -1),
 ('L', 1),
 ('M', -1),
 ('X', -1),
 ('Y', 1),
 ('O', 0),
 ('V', 0)]

In der obigen Lösung vergleichen wir die beiden Positionen i und j des Alphabets alphabet und der Häufigkeit char_freq indem wir die Distanz i-j berechnen. Wir speichern diese Distanzen in der Liste chars_diff und sortieren diese anhand des Betrags abs der Distanz.

S ist der Gewinner bzw. Verlierer gefolgt vom B und J. S ist deutlich zu weit hinten anzutreffen und die beiden anderen deutlich zu weit vorne. Im Fall des Alphabets, fällt uns kaum eine Situation ein in der das zum Nachteil wird. Doch ähnlich wie Dominique übersetzen auch wir physikalische Bewegungen in Buchstaben. Wir verwenden hierfür zum Beispiel die Tastatur!

Exercise 21.15 (Die perfekte Tastatur)

Sind die Buchstaben auf Ihre Tastatur für Sie optimal (entsprechend der Häufigkeit) angeordnet?

Es gäbe sicherlich eine effektivere Anordnung an Buchstaben. Unsere gängige Anordnung hat sich geschichtlich ergeben und wird Aufgrund der Gewohnheit nicht verändert. Wenn sie aber ein wenig Lebenszeit sparen wollen, lohnt es sich vielleicht Ihre eigene Anordnung zu verwenden. Niemand wird Sie davon abbringen, allerdings müssten Sie jedesmal Einstellungen vornehmen, wenn Sie an einen anderen Computer gehen. Vielleicht setzt sich aber Ihre Variante dann irgendwann einmal durch. 1930 hat sich dieser Aufgabe ein gewisser August Dvorak angenommen (siehe Dvorak-Tastaturbelegung).

Durch den Einsatz von Wissen und Struktur in der Form der Häufigkeit haben wir unseren Algorithmus für Dominique verbessert, zumindest aus technischer Sicht! Dennoch benötigen wir lediglich im Durchschnitt den halben Aufwand. Im schlimmsten Fall gewinnen wir gar nichts. Wir können uns nicht sicher sein, besser zu sein. Im folgenden werden wir uns überlegen durch welche Strategie wir einen bestimmten Aufwand garantieren können.

21.5. Suchalgorithmen#

Spielen wir ein Ratespiel! Ich denke mir eine berühmte Person aus und Sie müssen diese erraten. Sie dürfen 20 Ja-Nein-Fragen stellen die ich Ihnen wahrheitsgetreu mit Ja oder Nein beantworten muss.

Exercise 21.16 (Die perfekten Fragen)

Welche Art von Fragen würden Sie als gute Fragen bezeichnen und warum? Ist ‚Beginnt der Nachname mit einem A?‘ bzw. ‚Ist das Alter größer als 40?‘ eine gute bzw. schlechte Frage?

Mit jeder Ja-Nein-Frage zerteilen Sie die übrige Menge an Menschen in zwei Teilmengen. Falls diese Mengen gleich groß sind, bleibt, egal wie die Antwort ausfällt, die Hälfte übrig (oder ein Element mehr als die Hälfte). Bei \(16\) Elementen bleiben nach einer Frage noch \(16/2\) übrig. Nach zwei Fragen bleiben \((16/2)/2\) also \(16/2^2\) übrig. Allgemein bleiben nach \(k\) Fragen \(16/2^k\) Menschen übrig. Für \(2^k = 16\) bleibt genau eine Frage übrig und weitere Fragen sind überflüssig. Dieses \(k\) können wir mit

\[k = \log_2(16)\]

berechnen. Natürlich braucht es gute Fragen, aber dieses Teilproblem können wir aus dem Gesamtproblem herausziehen. Nehmen wir erst einmal an Sie fänden lauter gute Fragen - ein Vorgehen bei dem wir das Problem Zerlegen (Dekomposition) und uns jedem Teilproblem getrennt zuwenden.

Exercise 21.17 (Wie viele Fragen?)

Angenommen Sie hätten perfekte Fragen auf vorrätig. Wie viele Fragen brauchen Sie um die besagte Person zu erraten? Reichen 20 Fragen aus?

Das Fragespiel können wir auch als eine Suche interpretieren. In der Informatik werden Algorithmen, die eine bestimmte Menge absuchen als Suchalgorithmen bezeichnet. Die Strategie, in jedem Schritt in einer der Hälften der noch übrigen Menge weiterzusuchen, nennt sich binäre Suche. Würden wir jedes Element der Menge einzeln durchgehen, dann würden wir einer linearen Suche folgen.

Dadurch, dass wir durch die binär Suche die Menge in jedem Schritt halbieren, verringert sich die Anzahl der übrigen Elemente exponentiell und die notwendigen Schritte ist durch den Logarithmus beschrieben.

Solche Algorithmen gehören, was die Berechnungszeit angeht, zu den Kronjuwelen - viel besser geht es oftmals nicht!

Wie in Informationsrepräsentation bereits erwähnt, spielt die Basis des Logarithmus, also ob wir die Menge in zwei (\(\log_2\)), drei (\(\log_3\)), vier (\(\log_4\)) usw. Teile zerteilen keine so große Rolle, sobald die Menge nur groß genug ist.

Da der Logarithmus so langsam anwächst, benötigt unsere binäre Suche nahezu konstant viele Schritte. Was meinen wir damit? Nun wie sich gezeigt hat, reichen \(33\) Schritte um aus allen Menschen den oder die richtige zu identifizieren. Stellen Sie sich nun vor sie hätten einen anderen Algorithmus der egal wie groß die Menge ist, sagen wir konstant \(10000\) Schritte bräuchte. Erst wenn die Menge größer ist als \(2^{10000}\) benötigt unsere binäre Suche mehr Schritte. Doch eine solch unvorstellbar große Menge werden wir womöglich in der Praxis niemals zu Gesicht bekommen.

21.6. Binäre Buchstabensuche#

Wie können wir die binäre Suche auf Dominique’s Problem anwenden und garantieren, dass jeder Buchstabe den Dominique schreiben möchte den gleichen Aufwand hat, d.h. der Sprecher muss für jeden Buchstaben den Dominique ihm mitteilen will gleich viele Buchstaben aussprechen.

Exercise 21.18 (Binäre Buchstabensuche)

Entwerfen Sie einen Blinzel-Algorithmus, der für jeden Buchstaben den gleichen (geringen) Aufwand benötigt. Übertragen Sie dabei die binäre Suche (das Fragespiel) auf Dominique’s Problem sich auszudrücken. Wie viele Schritte benötigen Sie?

Mit 5 Schritten, sind wir im Durchschnitt besser als die lineare Suche, welche die Häufigkeit ausnutzt. Außerdem haben wir eine Garantie: wir benötigen niemals mehr als 5 Schritte!

Als Anwender von Algorithmen sind derartige Garantien sehr wertvoll, denn wir müssen oft vom schlechtesten Fall ausgehen.

Würden wir mehr und mehr Zeichen aufnehmen (z.B. Ziffern und Sonderzeichen) können wir leicht bestimmen wie das den Aufwand beeinflusst. Für eine Menge von \(n\) Elementen benötigt die binäre Suche

\[\log_2(n)\]

(aufgerundet) Schritte.

21.7. Repräsentation#

Möchte Dominique die binäre Suche einsetzen muss er natürlich Wissen welche Buchstaben jeweils in welcher Menge sind. Falls er ein P blinzeln will, muss er wissen in welchen Teilmengen sich das P befindet. Um zu dem Buchstaben P zu gelangen muss Dominique nach jedem gesagten Buchstaben blinzeln oder nicht blinzeln. Das P erhält er durch die Folge: nicht blinzeln, blinzeln, blinzeln, nicht blinzeln, blinzeln.

Wie Strom aus und Strom an gibt es zwei Zustände die jedes Element der Folge annehmen kann. Wir können nicht blinzeln als \(0\) und blinzeln als \(1\) interpretieren! Damit ergibt sich für P die Folge \(0, 1, 1, 0, 1\) oder schlicht das binäre Wort \(01101\). Eine andere Codierung ist natürlich auch möglich.

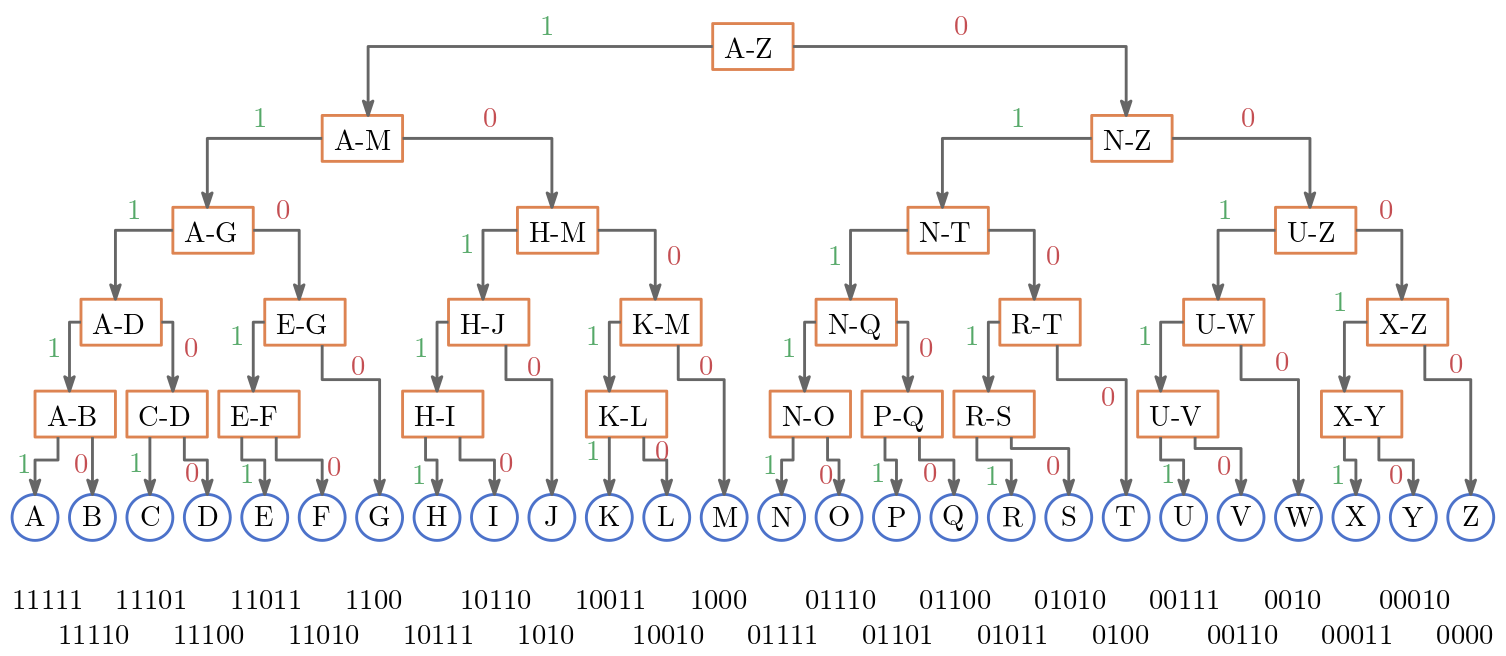
../../_images/alphabet-code-tree.png

Abb. 21.2 Binärer Such/Codierungsbaum#

Wir können jedem Buchstaben bzw. jedem Element aus der Menge ein eindeutiges binäres Wort zuweisen. Dies ergibt eine Codierung der Buchstaben.

Exercise 21.19 (Codierung des A)

Welches binäre Wort repräsentiert das A in unserer Codierung?

Wir könnten für Dominique eine Tabelle machen in der für jeden Buchstaben das entsprechende Codewort steht. So müsste er sich nichts merken! Wir könnten diese Tabelle händisch erzeugen, aber warum überlassen wir das nicht dem Computer?

Exercise 21.20 (Codierung erzeugen)

Schreiben Sie ein Programm, was für einen gegebenen Buchstaben das entsprechende Codewort erzeugt. Erzeugen Sie damit ein Dictionary codebook, wobei jeder Schlüssel ein Buchstabe und jeder Wert das entsprechende Codewort ist.

Tipp: Nehmen Sie als Grundlage eine Liste alphabet, die alle Buchstaben in der richtigen Reihenfolge enthält.

alphabet = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J',
            'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T',
            'U', 'V', 'W', 'X', 'Y', 'Z']

Ihr Codewort können Sie als Zeichenkette oder als Liste von \(0\), \(1\) modellieren. Überlegen Sie erst mit Stift und Papier wie sie vorgehen könnten. Sie können Zeichenketten oder einzelne Zeichen lexikographisch mit <, <=, > und >= vergleichen.

alphabet = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J',
            'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T',
            'U', 'V', 'W', 'X', 'Y', 'Z']

def code(letter, alphabet):
    code = []
    left = 0
    right = len(alphabet)-1
    k = int((right-left) / 2)
    while right-left > 0:
        if letter <= alphabet[k]:
            code.append(1)
            right = k
        else:
            code.append(0)
            left = k+1
        k = left + int((right-left)/2)
    return code

codebook = {}
for letter in alphabet:
    codebook[letter] = code(letter, alphabet)
    
codebook

{'A': [1, 1, 1, 1, 1],
 'B': [1, 1, 1, 1, 0],
 'C': [1, 1, 1, 0, 1],
 'D': [1, 1, 1, 0, 0],
 'E': [1, 1, 0, 1, 1],
 'F': [1, 1, 0, 1, 0],
 'G': [1, 1, 0, 0],
 'H': [1, 0, 1, 1, 1],
 'I': [1, 0, 1, 1, 0],
 'J': [1, 0, 1, 0],
 'K': [1, 0, 0, 1, 1],
 'L': [1, 0, 0, 1, 0],
 'M': [1, 0, 0, 0],
 'N': [0, 1, 1, 1, 1],
 'O': [0, 1, 1, 1, 0],
 'P': [0, 1, 1, 0, 1],
 'Q': [0, 1, 1, 0, 0],
 'R': [0, 1, 0, 1, 1],
 'S': [0, 1, 0, 1, 0],
 'T': [0, 1, 0, 0],
 'U': [0, 0, 1, 1, 1],
 'V': [0, 0, 1, 1, 0],
 'W': [0, 0, 1, 0],
 'X': [0, 0, 0, 1, 1],
 'Y': [0, 0, 0, 1, 0],
 'Z': [0, 0, 0, 0]}

Lassen Sie uns noch einmal rekapitulieren weshalb die binäre Suche anwendbar ist. Was wir voraussetzen ist, dass wir gute Fragen stellen können und, anhand jeder Antwort, die Menge schnell verkleinern können. Mit schnell meinen wir, dass es keinen großen Aufwand kostet! Wenn Sie beispielsweise in unserem Ratespiel die Frage nach dem Geschlecht stellen, sie aber erst einmal jeden Menschen betrachten müssen um das Geschlecht herauszufinden, ist diese Frage zu aufwendig zu beantworten. Im Fall der Buchstabencodierung, verwenden wir eine totale Ordnung der Buchstaben und können durch einen entsprechenden Vergleichsoperator die Buchstabenmengen immer weiter verfeinern, indem wir das Intervall der Buchstaben, die wir betrachten, verkleinern.

Wenn Sie sich unsere Lösung ansehen werden Sie vielleicht festellen, dass wir jede endliche Menge mit einer totale Ordnung codieren können, sofern der <=-Operator definiert ist. Zum Beispiel können wir Zahlen codieren:

numers = [1,2,3,4,5,6,7,8,9,10,11,12,13,14]
codebook = {}
for number in numers:
    codebook[number] = code(number, numers)
    
codebook

{1: [1, 1, 1, 1],
 2: [1, 1, 1, 0],
 3: [1, 1, 0, 1],
 4: [1, 1, 0, 0],
 5: [1, 0, 1, 1],
 6: [1, 0, 1, 0],
 7: [1, 0, 0],
 8: [0, 1, 1, 1],
 9: [0, 1, 1, 0],
 10: [0, 1, 0, 1],
 11: [0, 1, 0, 0],
 12: [0, 0, 1, 1],
 13: [0, 0, 1, 0],
 14: [0, 0, 0]}

21.8. Suchalgorithmen#

Anstatt ein Element zu codieren könnten wir es auch einfach nur suchen.

Exercise 21.21 (Binäre Suche)

Schreiben Sie anhand des obigen oder Ihres Codes eine Funktion binary_search(element, mylist) welche True zurückgibt, wenn element in mylist zu finden ist. Ansonsten soll die Funktion False zurückgeben. Gehen Sie davon aus, dass mylist geordnet ist und auf der Liste eine totale Ordnung sowie der <=-Operator definiert ist. Testen Sie Ihre Funktion mit einer Liste aus Zahlen und Buchstaben.

def binary_search(element, mylist):
    left = 0
    right = len(mylist)-1
    k = (right-left) // 2
    while right-left >= 0:
        if element == mylist[k]:
            return True
        if element < mylist[k]:
            right = k-1
        else:
            left = k+1
        k = left + (right-left) // 2
    return mylist[k] == element

print(binary_search('T',alphabet))
print(binary_search('t',alphabet))
print(binary_search(1,[1,2,3,4,5]))
print(binary_search(7,[1,2,3,4,5]))
print(binary_search(-7,[1,2,3,4,5]))

True
False
True
False
False

Die binäre Suche nutzt die gegebene Struktur der Daten (Information) aus, wohingegen die lineare Suche keinerlei Struktur nutzt. Besteht keinerlei ausnutzbare Struktur bleibt uns nichts anderes übrig als die lineare Suche zu verwenden.

Exercise 21.22 (Lineare Suche)

Schreiben Sie eine Funktion linear_search(element, mylist) welche True zurückgibt, wenn element in mylist zu finden ist. Ansonsten soll die Funktion Falsezurückgeben. Diesmal wissen Sie nichts über die Struktur der Daten!

def linear_search(element, mylist):
    for e in mylist:
        if e == element:
            return True
    return False

print(linear_search('T',alphabet))
print(linear_search('t',alphabet))
print(linear_search(1,[1,2,3,4,5]))
print(linear_search(7,[1,2,3,4,5]))
print(linear_search(-7,[1,2,3,4,5]))

True
False
True
False
False

Exercise 21.23 (Aufwandsvergleich)

Wie viel Aufwand/Schritte benötigen Sie im besten Fall und im schlechtesten Fall für

  1. die lineare Suche und

  2. die binäre Suche?

Der unterschiedliche Aufwand macht sich bemerkbar wenn \(n\) entsprechend groß wird.

Exercise 21.24 (Laufzeitvergleich)

Führen Sie nacheinander (getrennt voneinander) folgende Zeilen aus. Was beobachten Sie? Achten Sie darauf wie lange es dauert bis das Ergebnis ausgegeben wird. Wie groß ist jeweils der Aufwand?

n = 100_000_000
numbers = list(range(n))

print(linear_search(int(n/2),numbers))

print(binary_search(int(n/2),numbers))

Wir haben also zwei Algorithmen die für eine Eingabe mit bestimmten Vorraussetzungen zum gleichen Ergebnis führen, jedoch unterschiedlich schnell auf dem Computer ausgeführt werden. Blicken wir auf die Problemtypen welche die Algorithmen lösen können, ist die lineare Suche mächtiger bzw. genereller. Die binäre Suche kann nur eine Teilmenge der Probleme lösen ist jedoch, aufgrund der angenommen Struktur der Eingabe, deutlich effizienter. Diesem Sachverhalt werden Sie noch häufiger begegnen. Oft gibt es einen generellen Algorithmus der ein breites Spektrum an Problemen löst und speziellere Algorithmen, welche nur eine Teilmenge der Probleme lösen können, dafür aber deutlich effizienter sind.

21.9. Das Wesen der Technik#

Before you become too entranced with gorgeous gadgets and mesmerizing video displays, let me remind you that information is not knowledge, knowledge is not wisdom, and wisdom is not foresight. Each grows out of the other, and we need them all. - Arthur C. Clarke

21.9.1. Maschinelles Lernen#

Heute könnten wir eine kleine App schreiben mit der wir die Häufigkeit der Wörter bequem abspeichern. Wir könnten über Spracherkennungsalgorithmen einfach den Text, den Dominique uns zublinzelt hinein sprechen und die Software wäre in der Lage die Wörter zu extrahieren und eine Datenbank der Wörter mit ihrer Häufigkeit zu verwalten.

Wir wären heute in der Lage eine Software zu entwickeln, die erkennt wenn ein Mensch blinzelt. Über eine Kamera würden wir das Blinzeln aufzeichnen und ein trainierter Algorithmus (maschinelles Lernen) könnte darauf schließen, nicht nur ob jemand blinzelt, sondern auch wie schnell. Wir könnten konfigurieren, welchen Zeitraum wir als zweimal, keinmal oder einmal blinzeln ansehen. Die Software könnte natürlich auch gleich das Lernen der Sprache des Gegenüber übernehmen und ihm immer wieder Vorschläge machen.

Noch besser! Algorithmen könnten lernen welche Vorschläge gut und welche schlecht waren und aufgrund dieser Information immer besser werden. Sie könnten nicht nur lernen welche vorgeschlagenen Wörter zum Erfolg führten sondern auch in welchem Zusammenhang. Zum Beispiel könnten sie feststellen, dass vor Apfel sehr oft das Wort der steht.

Wir könnten Algorithmen entwickeln, die mehr als nur das Gesprochene/Geblinzelte speichern. Wie wäre es zum Beispiel mit dem Datum und der Uhrzeit? So könnte unser Algorithmus lernen, dass das Wort Schnee in einer bestimmten Jahreszeit häufiger vorkommt. Oder dass Dominique zwischen 18:00 und 19:00 Uhr über das Essen redet.

Zuerst hätte diese Software bzw. Maschine die einfache Arbeit des Zählens des Blinzeln übernommen. Doch aus dieser Automatisierung ergeben sich vielerlei neue Möglichkeiten. Natürlich entwerfen sich diese cleveren Algorithmen nicht von alleine. Sie als Computational Thinker*innen kommen auf solche Ideen und machen aus ihnen Realität.

Zu Zeiten in denen Dominique im Krankenbett lag, gab es diese technischen Möglichkeiten noch nicht. Es gab keine Smartphone-Apps oder eine Maschine die das Blinzeln erkennt. Nichtsdestotrotz haben sich bereits viele Jahre zuvor Computational Thinker*innen und Mathematiker*innen mit solchen cleveren Algorithmen beschäftigt. Die Grundlagen des heute in aller Munde klingenden maschinellen Lernens wurden bereits vor langer Zeit erschlossen. Doch hatte man damals schlicht nicht die Rechnerressourcen um derartig kostenintensive Algorithmen auszuführen. Die Arbeiten blieben fast schon unbeachtet - heute ist die breite Datenanalyse von sehr sehr vielen Daten (BigData) an allen Ecken unserer (Informations-)Welt anzutreffen. Neben der Rechnerressourcen ist die Datenerhebung heute deutlich einfacher und hat Ausmaße angenommen, die uns in manchen Bereichen zu denken geben sollte.

21.9.2. Der verlängerte Arm#

An diesem Beispiel sehen wir, dass Algorithmen das Leben vereinfachen können und unnötige Erschwernisse eliminieren können. Im besten Fall, wie im Fall des Dominique, emanzipieren sie Anwender*innen. Aber selbst in seinem Fall hätte diese Erleichterung womöglich auch Nachteile für ihn gehabt. Hätte Dominique durch die Maschine im Endeffekt weniger menschlichen Kontakt erfahren? Er hätte schließlich die Möglichkeit gehabt ganze Briefe/E-Mails zu schreiben oder sich durch soziale Medien auszutauschen. Der Bequemlichkeit wegen hätte man mit ihm vielleicht mehr und mehr durch Text kommuniziert, da man es vielleicht leid gewesen wäre, durch seine langsame Kommunikation ausgebremst zu werden. Andererseits hätte Dominique wieder an Diskussionen teilnehmen können. Durch die vorgeschlagenen Wörter, hätte sich mit der Zeit womöglich sein Wortschatz verringert. Andererseits wäre er durch die Erleichterungen womöglich motiviert gewesen komplizierte Wörter und Sätze zu bilden.

Technologie betrachten wir gerne als etwas von uns getrenntes. Als etwas das wir jederzeit ablegen können, wenn wir möchten. Der hier konstruierte Fall des Dominique zeigt jedoch, dass Technik zum verlängerten Arm werden kann - ein Arm der fest verwachsen ist und unsere Handlungen mitbestimmt. In Science Fiction Filmen und Büchern wie Ghost in the Shell verschmilzt Technik buchstäblich mit dem Menschen. Da gibt es verwachsene Roboterarme, implantierte Mikrochips für verbesserte kognitive Fähigkeiten und vieles mehr. Hier ist die Trennung zwischen Mensch und Maschine fließend - das Bewusstsein (der Ghost) ist in einer Hülle (Shell). Aber verhält es sich mit weniger ausgeklügelter Technik nicht ebenso? Ich wage zu behaupten, dass der Hammer eines Handwerkers, der Bogen eines Jägers oder das Smartphone von heute, zwar in einer anderen Tiefe aber dennoch ähnlich mit dem Menschen verwoben sind/waren wie die implantierten Mikrochips aus Ghost in the Shell.

Das ist im Allgemeinen weder gut noch schlecht doch sollten wir uns dessen bewusst sein. Technik ist mehr als ein neutrales Werkzeug außerhalb von jedem Kontext. Technik interagiert mit uns, verändert uns. Wir interagieren mit ihr und durch sie hindurch, wiederum mit uns. Technik verändert Gesellschaften und Wirtschaftssysteme. So führte das Automobil dazu, dass insbesondere in den USA Geschäfte sich an bestimmten Orten konzentrierten und so jeder auf ein Auto angewiesen war. Heute tragen Informationssysteme zu den wesentlichsten gesellschaftlichen, kulturellen und wirtschaftlichen Veränderungen bei.

Während des Hämmerns ist für den Handwerker der Hammer unsichtbar, er ist sein verlängerter Arm. Auch für uns ist vieles unsichtbar. Und wie es dem Handwerker zugute kommen kann über das Wesen des Hammers nachzudenken, kann es uns zugute kommen über das Wesen von Algorithmen und Informationssysteme nachzudenken.

21.10. Der Mensch im Zentrum#

Entwickeln wir neue Algorithmen und Informationssysteme für eine(n) Anwender*in sollte der Mensch im Zentrum stehen. Wenn Dominique mit unserer verbesserten Variante der Kommunikation nicht so gut zurechtkommt oder mit dieser schlicht nicht zurechtkommen will, aus welchen Gründen auch immer, dann ist sie für ihn nutzlos. Möchten wir Dominique helfen, müssen wir uns zuallererst mit ihm auseinandersetzen, mit ihm kommunizieren und herausfinden was er braucht und möchte und was eben nicht.

Ist die Anwenderschaft groß bzw. breit aufgestellt, gilt dies ebenso. Allerdings gestaltet sich die Beantwortung dieser Fragen dann als viel schwieriger. Hinzu kommt, dass wir uns fragen sollten welche Auswirkungen unsere Anwendung, nicht nur auf die Anwenderschaft, sondern eben auch auf jene Menschen hat, die sich von unserer Anwendung, aus verschiedenen Gründen, fernhalten wollen oder müssen. Gründe hierfür gibt es viele. Möglicherweise fehlt manchen Menschen der Zugang, sei es wegen kognitiver oder physischer Gegebenheiten, finanziellen Mittel oder weil Dienste nicht angeboten werden. Andere sehen in der Anwendung eine Gefahr oder möchten sie, aus welchen Gründen auch immer, nicht nutzen.

Neue Technik der Technik wegen, kann und sollte nicht unser Anspruch sein. Stattdessen sollte Technik den Menschen emanzipieren.