Datenstrukturen

10.4. Datenstrukturen#

Programmiersprachen und deren Standardbibliotheken bieten viele vordefinierte Datentypen und Datenstrukturen. In diesem Abschnitt wollen wir über die fundamentalsten Datenstrukturen sprechen. Wir werden Ihnen dabei auch eine Python-Implementierung präsentieren, die Sie sich rückwirkend ansehen können, sobald Sie genug Erfahrung mit Python gesammelt haben. Für eine weiterführende und zugleich angewandte Diskussion verweisen wir auf das Kapitel Datentypen (Grundlagen) und Datentypen (Fortsetzung) des PYTHON-Teils.

Eine Datenstruktur strukturiert Daten. Sie dient der Organisation von Daten. Eine Form einer Datenstruktur liefert beispielweise die Struktur eines Briefs. Die Vorgaben wie ein Brief zu schreiben ist, d.h. dessen Strutukr, organisiert seine Daten (Absender, Empfänger, Betreff, Datum, Botschaft, usw.) auf einem oder mehreren Blättern Papier. Dabei ist jedoch vordefiniert welche Daten (von welchem Datentyp) strukturiert werden. Ein solche solche Struktur wird in vielen Programmiersprachen durch Klassen realisiert. Diese besprechen wir im Kapitel Objektorientierte Programmierung.

In diesem Abschnitt wollen wir uns stattdessen mit Datenstrukturen beschäftigen, die prinzipiell unterschiedlich viele und oftmals auch beliebige Daten strukturieren. Wir kennen solche Datenverwaltungsstrukturen aus der physikalischen Welt: Ordner, Schnellhäfter, Schließfächer, Warteschlangen, Räume und Sitzpätze sind, unter bestimmter Betrachtung, Datenstrukturen. Ein Ordner strukturiert Dokumente (z.B. Briefe). Warteschlangen, Räume und Sitzplätze ordnen Menschen. Schließfächer strukturieren unterschiedliche Objekte in einer bestimmten Reihenfolge. Solche Datenstrukturen bezeichen wir als Sammlung (engl. Collection).

10.4.1. Arten von Sammlungen#

Da sich alle Daten (Programm und dessen Eingabe/Ausgabe) im Arbeitsspeicher befinden, müssen wir begreifen welche Funktionalität diese konkrete Datenstruktur bietet. Alle weiteren abstrakten Datenstrukturen bauen auf diesen Möglichkeiten auf.

Über die Geschichte hinweg hat sich der Arbeitsspeicher in Geschwindigkeit und Größe und bezüglich anderer Eigenschaften weiterentwickelt. Was uns jedoch interessiert sind die wenigen grundlegenden Eigenschaften, die wir als Programmierer*in beachten müssen:

Ordnung: Der Arbeitsspeicher ist im Wesentlichen eine lange geordnete Ansammlung an Bits
Addressierbarkeit: Diese Bits sind addressierbar/indexierbar
Effizienz: Die Adressierung eines Bits für eine gegebene Adresse ist sehr effizient

Die Eigenschaft der effizienten Adressierung spiegelt sich in allen Programmiersprachen mehr oder weniger pregnannt wieder. Gewöhnlich adressiert die CPU keine einzelnen Bits, sondern ein ganzes Byte. Abbildung 10.4 zeigt ein Beispiel eines Arbeitsspeichers der uns erlaubt jeweils ein Byte zu adressieren. Zugleich werden Adressen, in diesem Beispiel, durch ein Byte dargestellt.

Es gibt zwei wesentliche Arten, wie Datenstrukturen im Arbeitspeicher realisiert werden:

(1) Statische Sammlungen: Die Sammlung liegt als zusammenhängende Folge von Bits im Arbeitsspeicher
(2) Dynamische Sammlungen: Die Sammlung besteht aus mehreren zusammenhängenden Folgen von Bits, die voneinander getrennt im Arbeitsspeicher liegen.

10.4.1.1. Statische Sammlungen#

Das Prinzip ist einfach: Die Datenstruktur, inklusiver ihrer Elemente, wird durch einen zusammenhängenden Speicherbereich realisiert.

Exercise 10.4 (Schließfächer)

Stellen Sie sich den Arbeitsspeicher als eine Ansammlung von nummerierten Schließfächern vor. Angenommen Sie können frei über diese Schließfächer bestimmen. Sie wollen 10 Gegenstände, wobei jedes dieser Gegenstände den Platz von einem Schließfach verbraucht, lagern. Mit welcher Strategie müssen Sie sich am wenigsten merken um ihre Gegenstände wiederzufinden?

Solution to Exercise 10.4 (Schließfächer)

Sie wählen ein beliebige Schließfach (nicht zu weit hinten) aus und legen alle Gegenstände in aufeinderfolgende Schließfächer ab. Sie müssen sich lediglich die Nummer des einen Schließfachs und die Anzahl der Gegenstände merken.

Die Aufgabe verrät uns den wesentlichen Vorteil, wenn wir Daten im Verbund, d.h. in einem zusammenhängenden Speicherbereich ablegen. Es ist uns möglich diese Daten sehr einfach wiederzufinden. Wir müssen uns nur eine Speicheradresse merken!

Wollen wir, z.B., die Ziffern einer ISBN-Nummer abspeichern, so könnten wir diese Ziffern nebeneinander im Speicher ablegen. Wir merken uns bei welcher Adresse die ISBN-Nummer beginnt und wie viele Stellen sie hat. Eine solche Datenstruktur realisiert das sog. Array oder die Python-Liste.

Datenstrukturen realisiert als zusammenhängender Speicherbereich haben Vor- und Nachteile, welche uns das Schließfachbeispiel gut veranschaulicht. Wenn Sie, z.B., auf den dritten Gegenstand (wir beginnen bei 0) zugreifen wollen, können Sie das Schließfach in Windeseile auffinden. Sie gehen zum Schließfach dessen Nummer Sie kennen und wandern dann vier Schließfächer nach, z.B. rechts. Da jedes Schließfach gleich breit ist, müssen Sie nicht einmal auf die anderen Schließfächer blicken und können einen großen Schritt der Lämge 4 mal \(c\) Meter nach z.B. rechts wandern. Sie können den Abstand zwischen dem 0-ten und 3-ten Gegenstand (mit einfachen arithmetischen Mitteln) berechnen.

Genauso verhält es sich mit den Adressen des Speichers. Kennen wir die Adresse \(x_0\) des 0-ten Elements/Gegenstands und wissen wie viele Bits jeder Gegenstand verbraucht, sagen wir \(c\) Bits, können wir die Adresse des \(i\)-ten Elements durch

\[x_i = x_0 + c \cdot i\]

berechnen. Deshalb ist die Indexierung eines Elements enorm effizient. Vorraussetzung ist jedoch, dass jedes Element durch genau \(c\) Bits repräsentiert wird. Die folgende Abbildung veranschaulicht die Indexierung. Dabei ist in blau der von der Datenstruktur belegte Speicher hervorgehoben. Die grauen Bereiche sind ebenfalls belegt jedoch nicht von unserer Datenstruktur.

Was aber wenn Sie einen weiteren Gegenstand in den Zusammenschluss aus Schließfächern einfügen wollen und zwar mitten drinnen? Dann müssen Sie viele Gegenstände aus Schließfach \(k\) in das Schließfach \(k+1\) bewegen. Folgende Abbildung skizziert diesen aufwendigen Vorgang:

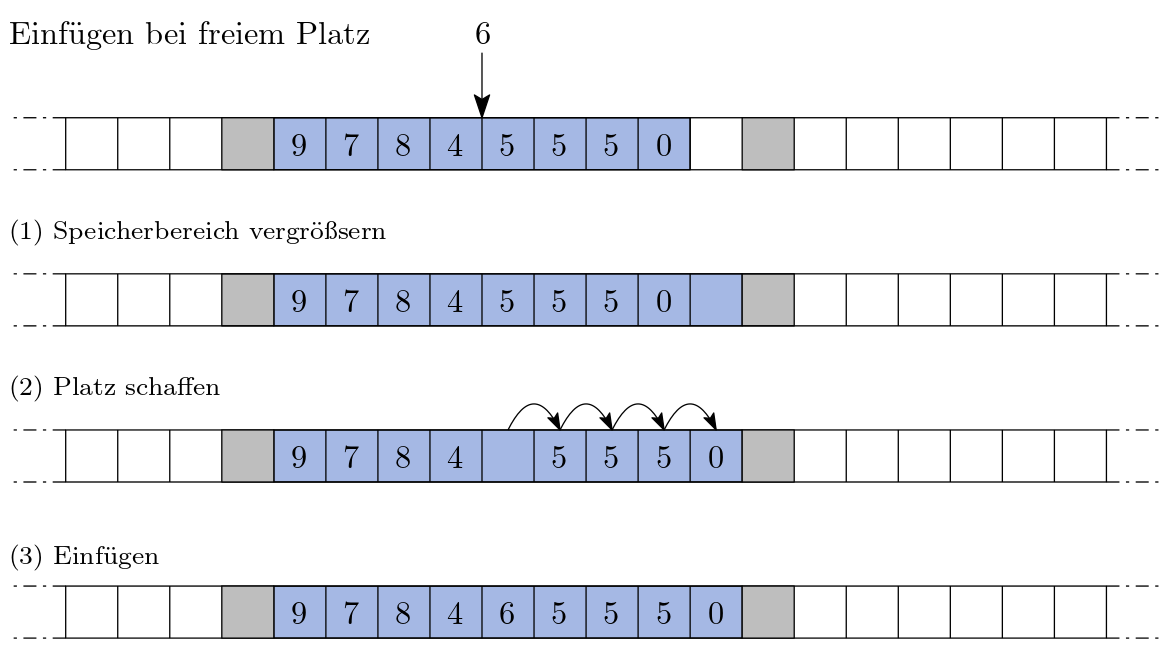
Und was passiert wenn das darauffolgende Schließfach von jemandem anderen belegt ist? Dann müssten Sie alle Gegenstände in eine neue Folge aus zusammenhängende Schließfächer befördern Sie müssen dafür natürlich eine Stelle finden, die genug Platz bietet! Die folgende Abbildung skizziert diesen Vorgang:

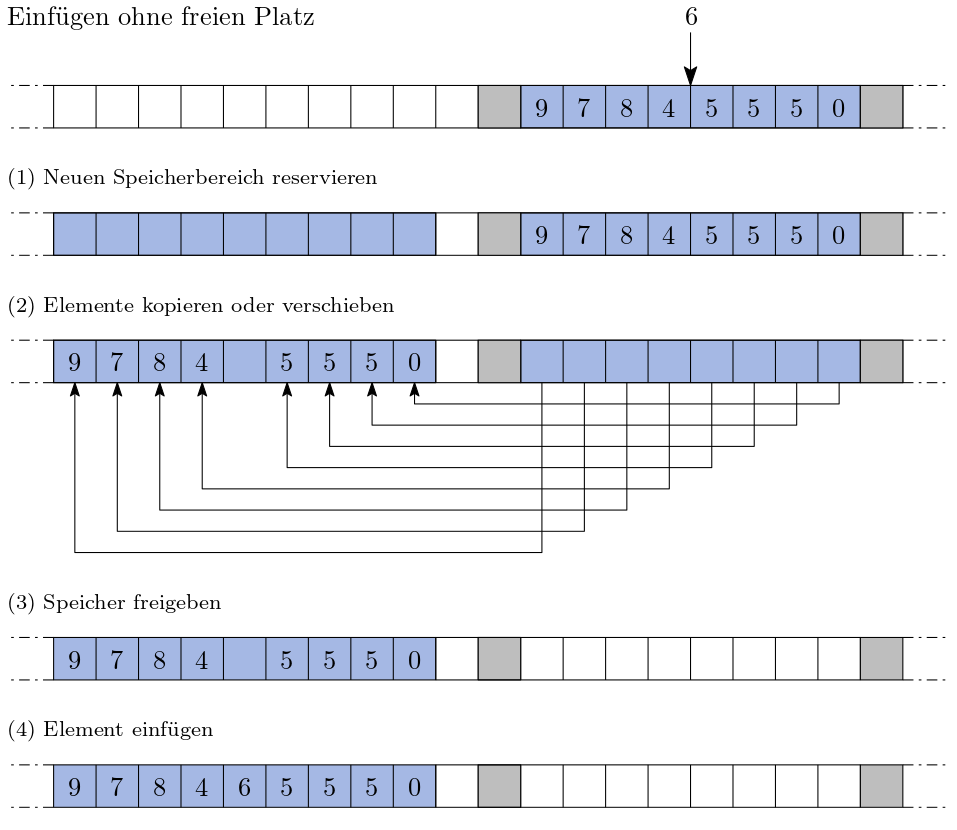
Wenn Sie einen Gegenstand inmitten der Schließfächer löschen, müssen Sie ebenfalls viele Gegenstände bewegen. Dieser Vorgang ähnelt dem Einfügen inmitten der Datenstruktur.

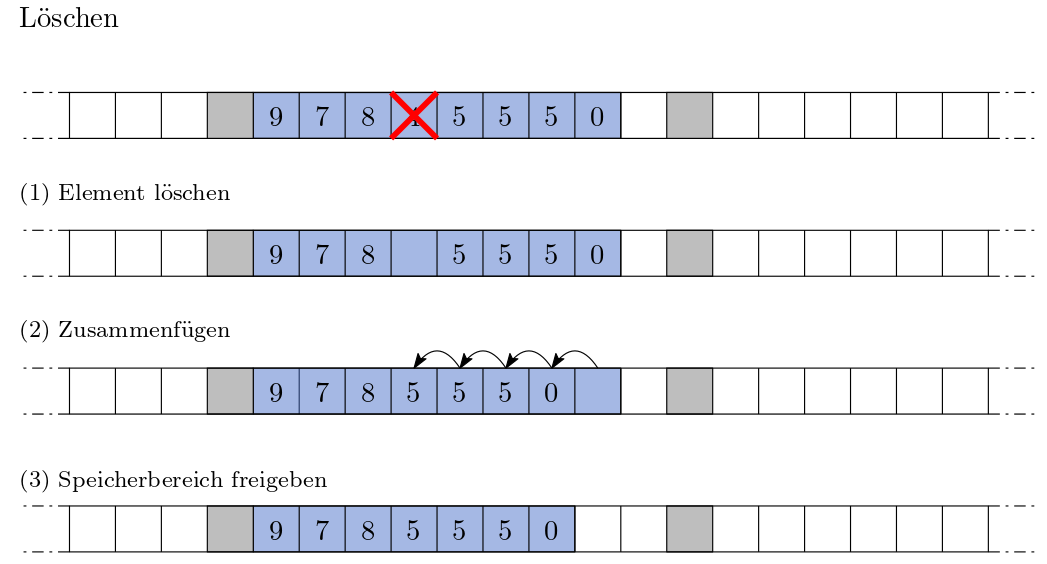
Die Vorteile zeigen Effizienz beim Zugriff über einen Index. Die Nachteile offenbaren dagegen die Unflexibilität bei der Veränderung der Größe der Datenstruktur.

Statische Sammlungen

Statische Sammlungen können zur Laufzeit des Programms ihre Größe nicht verändern, d.h. ihr Speicherverbrauch kann sich nicht verändern. Stattdessen muss ein eine neue Datenstruktur angelegt werdeb.

Aus diesem Grund ist ein Arraya eine statische Sammlung, d.h. deren Speicherverbrauch muss bei ihrer Erzeugung festgelegt sein und kann sich nicht dynamisch, also während der Laufzeit, ändern. Das heißt, Sie reservieren einmalig Ihre \(n\) nebeneinander liegenden Schließfächer und können an diesem Verbund nichts mehr ändern. Sie können zwar Gegenstände vertauschen oder ersetzten, doch kann Ihr Verbund niemals mehr als \(n\) Gegenstände enthalten!

10.4.1.2. Dynamische Sammlungen#

Anstatt die Sammlung durch einen zusammenhängenden Speicherbereich zu realisieren, gibt es eine zweite Möglichkeit: Die Realisierung über einen fragmentierten Speicherbereich, d.h. mehrere voneinander getrennte Speicherbereiche ergeben als zusammenschluss die Sammlung. Die Daten der Datenstruktur können somit Kreuz und Quer im Speicher liegen.

Das erhöht die Flexibilität! Die Datenstruktur kann durch Speicherbereiche anwachsen die eben nicht zusammenhängen. Dadurch müssen wir Elemente nicht fortwährend verschieben. Die Sammlung kann dynamisch anwachsen und schrumpfen.

Dynamische Sammlungen

Dynamische Sammlungen können zur Laufzeit des Programms anwachsenden und schrumpfen, d.h. ihr Speicherverbrauch kann sich verändern. Möglich wird dies durch die Verwendung von Zeigern.

Damit die fragmentierten Teile als ganzes repräsentiert werden können, müssen sie verbunden werden. Dies wird durch sog. Zeiger/Pointer realisiert. Oft spricht man auch von einer Referenz. Dabei ist wichtig, dass ein Zeiger wiederum auf einen weiteren Zeiger zeigen/verweisen/referenzieren kann.

Zeiger

Ein Zeiger ist ein Objekt welches eine Speicheradresse repräsentiert. Programmiersprachen bieten die Mittel um Zeiger aufzuösen, was den Zugriff auf das Objekt auf das sie verweisen ermöglicht.

Ein Zeiger verbraucht selbstverständlich auch Speicher. Er liegt selbst an irgendeiner Speicheradresse und benötigt mindestens soviele Bits, die wir zur Repräsentation aller Adressen benötigen. Ist der Arbeitsspeicher 8 Byte groß und nehmen wir an wir können jeweils ein ganzes Byte addressieren, dann brauchen wir 8 Adresse. Somit verbraucht jede Adresse \(\left \lfloor{\log_2(8)}\right \rfloor = 3\) Bits.

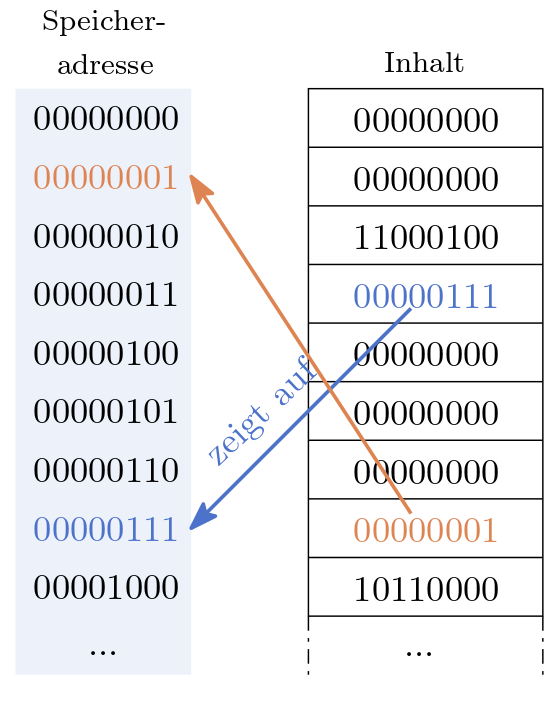
../../_images/ram.png — Abb. 10.4 Der Arbeitsspeicher ist eine sehr lange Liste bestehend aus Bits. Die Adresse (links) ist im Wesentlichen die Nummer / der Index eines bestimmten Speicherplatzes (rechts). Alle Werte sind im Binärsystem dargestellt. An Adresse 00000111 befindet sich eine Adresse.#

Exercise 10.5 (Adressraum)

Wie viel Byte können im Beispiel von Abbildung 10.4 maximal adressiert werden?

Solution to Exercise 10.5 (Adressraum)

Der Adressraum geht von \(0000\,0000_2\) bis \(1111\,1111_2\). Das heißt von \(0_{10}\) bis \(1\,0000\,0000_2 - 1_2 = 2^8-1 = 256-1 = 255\). Da jede Adresse ein Byte adressiert, können wir somit lediglich \(256\) Byte adressieren.

Exercise 10.6 (32-Bit-Adressraum)

Weshalb war es vor Jahren nicht möglich mehr als ca. 4 GiB Arbeitsspeicher im Rechner zu verwenden?

Hinweis: Es ereignete sich ein Wechsel von einer 32-Bit auf eine 64-Bit Adressierung.

Solution to Exercise 10.6 (32-Bit-Adressraum)

Mit \(32\) bildet sich ein Adressraum von \(2^{32}\) Adressen. Wenn die CPU jedes einzelne Byte adressieren können soll, so ergibt sich ein Maximum an

\[2^{32} \cdot 1 = 2^{10} \cdot 2^{10} \cdot 2^{10} \cdot 2^2\]

Byte und das sind \(2^{10} \cdot 2^{10} \cdot 2^2\) KiB, \(2^{10} \cdot 2^2\) MiB bzw. \(4\) GiB.

In Abbildung 10.4 zeigt der Zeiger an Adresse 3 auf den Speicherbereich bei Adresse 7. Dies ist wiederum eine Adresse die auf den Speicherbereich 1 zeigt und dort liegt der Wert 0. Selbstverständlich bedarf es der richtigen Interpretation der jeweiligen Speicherbereiche, denn es könnte sich beim Wert bei Adresse 3 auch um den Dezimalwert 7 oder irgendetwas anderes als einen Zeiger handeln.

Für Zeiger gibt es keine perfekte Analogie aus der Realwelt, jedenfalls ist uns keine eingefallen. Probieren wir es mit unserer Schließfachanalogie: Nehmen sie eine große geordnete Anreihung von Schließfächer als Arbeitsspeicher. Jedes Schließfach hat eine eindeutige Nummer (Speicheradresse). In jedem Schließfach kann sich etwas befinden, unter anderem auch ein Zettel mit einer Schließfachnummer (Zeiger).

Das Problem an dieser Analogie ist jedoch, dass, wenn wir den Zettel in Händen halten, wir erst zum entsprechenden Schließfach gehen müssen. Dabei laufen wir an vielen anderen Schließfächern vorbei. Das kostet Zeit. Wenn wir allerdings einen Zeiger haben, so können wir auf den Wert unglaublich schnell zugreifen. Es kostet der CPU zwar auch etwas Zeit (bzw. Zyklen) um den Zeiger aufzulösen aber muss sie nicht über alle dazwischenliegenden Speicherbereiche „hinweglaufen“, d.h. iterieren.

Ein Zeiger ähnelt einer Schnur die sich zwischen zwei Schließfächern befindet. Bei Aktivierung des Zeigers werden wir direkt vom einen Schließfach zum anderen teleportiert! Allerdings funktioniert dies nur in eine Richtung. Die Schnur ist gerichtet!

In den meisten Programmiersprachen wird die Handhabung von Zeigern durch Variablen abgebildet. In Hochsprachen wie Python müssen sich Programmierer*innen um Speicheradressen, das Reservieren und Freigeben von Speicher nicht kümmern. Das übernimmt der sog. Garbage Collector. Wie Python Variablen durch Zeiger realisiert erfahren sie im Abschnitt Variablen.

10.4.2. Einfach verkette Liste#

Wie können wir mit Zeigern eine Datenstruktur aus einem fragmentierte Speicherbereich bilden? Bleiben wir bei der Analogie der Schließfächer und Schnüre. Sie möchten ihre Lieblingsgerichte in alphabetischer Reihenfolge abspeichern. Dazu verwenden Sie die Schließfächer und Schnüre. Sie halten eine Schnur in den Händen, die auf das Schließfach mit Ihrem absoluten Lieblingsgericht zeigt. Das darauffolgende Schließfach verweist auf ihr zweitliebstes Gericht usw. Die so verketteten Schließfächer bilden eine sog. verkette Liste (engl. Linked List).

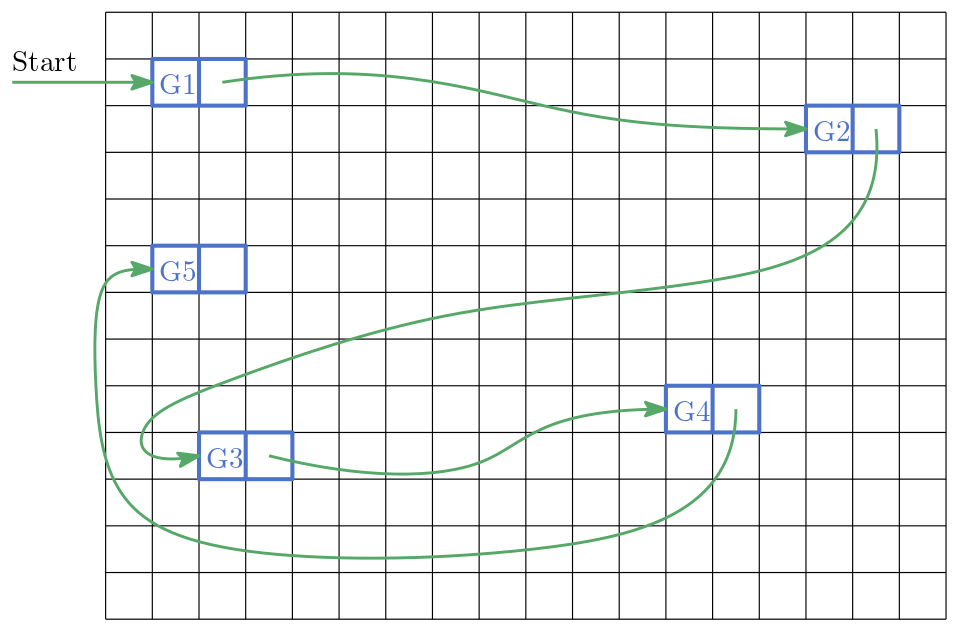
../../_images/linked-list-ram.png — Abb. 10.5 Gerichte 1 bis 5 in einer *verketteten Liste*. Jede Kachel repräsentiert ein Schließfach bzw. einen adressierbaren Speicherbereich.#

Befinden Sie sich an einem Schließfach der Liste, so können Sie recht einfach ein neues Element an dieser Stelle einfügen. Eine verkettete Liste besteht aus sogenannten Knoten (Schließfach + Schnur zum nächsten Schließfach), welche durch Zeiger verbunden sind. Sie ist eine dynamische Sammlung, d.h. sie kann zur Laufzeit vergrößert und verkleinert werden.

Haben wir direkten Zugriff auf einen Knoten so können wir in die verkettete Liste ein neues Element, was direkt nachfolgt, effizient einfügen ohne dabei die anderen Elemente der Liste zu verschieben – ein wesentlicher Vorteil dieser Datenstruktur. Jeder Knoten besteht aus zwei Teilen:

Daten: Der Wert des Knotens (oder auch ein Zeiger auf den Wert des Knotens). Das ist der Inhalt des Schließfachs.
Zeiger: Verweist auf den nächsten Knoten. Das ist die Schnur, die zum nächsten Schließfach führt.

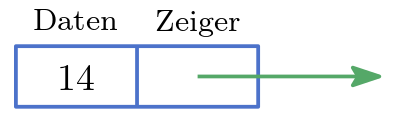
../../_images/linked-list-node.png — Abb. 10.6 Knoten einer *verketteten Liste*.#

class Node:
    def __init__(self, value, successor=None):
        self.value = value
        self.successor = successor
        
    def __repr__(self):
        return repr(self.value)

Den Anfangsknoten der Liste bezeichnet man als Kopf/Head.

../../_images/linked-list.png — Abb. 10.7 Einer *verkettete Liste* aus Zahlen.#

Um Elemente am Ende (engl. Tail) einzufügen, kann es sinnvoll sein sich zusätzlich den letzten Knote der Liste zu merken.

10.4.3. Der Stapel#

10.4.3.1. Eigenschaften#

Der Stapel (engl. Stack) oder auch Stapelspeicher/Keller ist einer der einfachsten dynamischen Sammlungen, welche dem Last-In-First-Out (LIFO) Prinzip folgt. LIFO bedeutet soviel wie: zuletzt hinein - zuerst heraus. Das was zuletzt hinein gekommen ist, wird auch als erstes herausgenommen. Das beudeutet, dass wir eingefügte Elemente nur in umgekehrter Reihenfolge aus dem Stapel herausnehmen können. Gleichbedeutend ist der Begriff Last Come, First Serve, d.h. wer zuletzt kommt wird zuerst bedient.

Wie der Stapel intern funktioniert ist nicht genau definiert, jedoch ist garantiert, dass die Datenstruktur die folgenden Operationen anbietet.

Operation	Laufzeit	Beschreibung
`size`	\(\mathcal{O}(1)\)	Liefert Anzahl der Elemente
`push(element)`	\(\mathcal{O}(1)\)	Legt das Element `element` auf den Stapel
`peek()`	\(\mathcal{O}(1)\)	Liefert das Element zurück, welches ganz oben auf dem Stapel liegt
`pop()`	\(\mathcal{O}(1)\)	Liefert das oberste Element des Stapels zurück und löscht es von diesem

All diese Operationen müssen eine gute Laufzeit haben. Man sagt auch, ihre (Zeit-)Komplexität ist konstant, d.h. von der Anzahl der Elemente (size) unabhängig, oder kurz \(\mathcal{O}(1)\).

Stellen Sie sich einen Stapel aus Büchern vor. Das Buch was Sie zuletzt auf den Bücherstapel gelegt haben liegt zugriffsbereit ganz oben. Um auf die anderen Bücher zuzugreifen ohne den Stapel komplett zu zerstören, müssen Sie sich von oben nach unten durcharbeiten und alle Bücher bis zu dem gewünschten Buch vom Stapel nehmen.

Wann könnte diese Datenstruktur sinvoll einsetzbar sein? Stellen Sie sich vor Sie laufen durch eine fremde Stadt. Sie orientieren sich anhand von Straßennamen. Um wieder zurückzufinden laufen Sie diese markanten Stellen in umgekehrter Reihenfolge ab. Sie können mit einem Stapel auch die Reihenfolge einer Serie von Elementen verändern. Das Ein- und Austreten aus einem Bus können wir durch einen Stapel modellieren.

10.4.3.2. Beispielimplementierung#

Für die genaue Realisierung eines Stapels gibt es viele Möglichkeiten. Eine davon stellt die Realisierung der einfach verketteten Liste mit einem Head dar:

# Last In
stack = Stack()
print(f'{stack}\n')
stack.push('A')
print(f'{stack}\n')
stack.push('B')
print(f'{stack}\n')
stack.push('C')
print(stack)

=>

=>'A'

=>'B'
  'A'

=>'C'
  'B'
  'A'

# First Out
while stack.size > 0:
    stack.pop()
    print(f'{stack}\n')

=>'B'
  'A'

=>'A'

=>

Wollen wir testen ob ein geklammerter Ausdruck z.B. '([3+2]+6)' richtig geklammert ist, können wir einen Stapel einsetzten, denn ist die \(i\)-te Klammer eine offene, muss die \(n-i-1\)-te eine geschlossene sein. Dabei ist \(n\) gleich der Anzahl der Klammern. Wir notieren uns die Klammern während wir den Ausdruck lesen, doch wann immer wir eine geschlossene Klammer lesen, löschen wir eine offene auf dem Stack. Befindet sich keine offene oder die falsche Klammer auf dem Stack, so ist der Ausdruck fehlerhaft. Die folgende Funktion parse bedient sich eines Stapels. Sie testet ob die Klammerung korrekt ist.

def parse(expression):
    stack = Stack()
    for c in expression:
        if c == '(' or c == '[':
            stack.push(c)
        elif c == ')':
            if stack.size == 0 or stack.peek() != '(':
                return False
            else:
                stack.pop()
        elif c == ']':
            if stack.size == 0 or stack.peek() != '[':
                return False
            else:
                stack.pop()
    if stack.size > 0:
        return False
    return True

print(parse('(3+5)*2'))                 # korrekt
print(parse('([3+5]*(2))'))             # korrekt
print(parse('(3+5)*2]'))                # falsch
print(parse('([3+5)*2]'))               # falsch
print(parse('()()()[]((([()])))'))      # korrekt
print(parse('()()()()((((())))'))       # falsch

True
True
False
False
True
False

10.4.4. Die Warteschlange#

10.4.4.1. Eigenschaften#

Die Warteschlange (engl. Queue) ist eine dynamische Sammlung und folgt dem sog. First-In-First-Out (FIFO) Prinzip. FIFO bedeutet soviel wie: zuerst hinein - zuerst hinaus. Das was zuerst hinein gekommen ist, wird auch als erstes herausgenommen. Das beudeutet, dass wir eingefügte Elemente nur in der gleichen Reihenfolge aus der Queue herausnehmen können. Gleichbedeutend ist der Begriff First Come, First Serve, d.h. wer zuerst kommt mahlt zuerst.

Wie die Warteschlange intern funktioniert ist nicht genau definiert, jedoch ist garantiert, dass die Datenstruktur die folgenden Operationen anbietet.

Operation	Laufzeit	Beschreibung
`size`	\(\mathcal{O}(1)\)	Liefert Anzahl der Elemente
`enqueue(element)`	\(\mathcal{O}(1)\)	Fügt das Element `element` hinten an
`dequeue()`	\(\mathcal{O}(1)\)	Liefert Element an forderster Stelle und löscht dieses aus der Struktur

All diese Operationen müssen eine gute Laufzeit haben. Man sagt auch, ihre (Zeit-)Komplexität ist konstant, d.h. von der Anzahl der Elemente (size) unabhängig, oder kurz \(\mathcal{O}(1)\). Der \(i\)-ten dequeue Aufruf liefert genau das Element, welches beim \(i\)-ten enqueue Aufruf von eingefügt wurde.

Der Name rührt daher, dass die Datenstruktur wie eine Warteschlange an der Kasse funktioniert. Kunden die sich zuerst in die Schlange einreihen, werden auch zuerst bedient und können die Schlange auch zuerst wieder verlassen. Wegen dieser Eigenschaft werden Queues oft als Puffer eingesetzt. Zum Beispiel werden die Netzwerkpakete die Ihr Router versendet erst in einer Queue gehalten und dann gesendet.

10.4.4.2. Beispielimplementierung#

Erneut gibt es unterschiedliche Möglichkeiten diese Datenstruktur zu realisieren. Glücklicherweise können wir abermals auf die einfach verketteten Liste zurückgreifen. Allerdings ist es notwendig sowohl auf den Kopf (Head) als auch auf das Ende (Tail) der Liste effizient zugreifen zu können. Deshalb merken wir uns, und verwalten zusätzlich das Ende der Liste, d.h. den (Tail).

Lassen Sie uns die Warteschlange fülle

queue = Queue()
queue.enqueue(1)
queue.enqueue(2)
queue.enqueue(3)
queue.enqueue(4)
queue

[1 => 2 => 3 => 4]

und wieder leeren.

for _ in range(queue.size):
    print(queue.dequeue())

10.4.5. Doppelt verkettete Liste#

10.4.5.1. Eigenschaft#

Die doppelt verkettete Liste (engl. Dequeue) ist einer Erweiterung der einfach verketteten Liste und zugleich eine Kombination aus Warteschlange und Stack. Sie besteht aus Knoten, die nicht nur einen Zeiger auf den nächsten, sondern auch auf den vorherigen Knoten enthalten. Das macht die Liste flexibler und die Verwaltung auch etwas aufwendiger. Es lassen sich effizient vorne und hinten Elemente einfügen und löschen. Außerdem können wir die Liste vorwärts und rückwärts durchlaufen. Da es mehr Zeiger zu setzten bzw. umzubiegen gibt, ist der Verwaltungsaufwand größer.

Um einen neuen Knoten hinter einem gegebenen Knoten anzuhängen append müssen wir lediglich die Zeiger richtig „verbiegen“. Auch diese Operation ist, bezogen auf die Laufzeit, sehr günstig. Wollen wir testen ob die Liste einen bestimmten Wert enthält contains, so müssen wir diese von Kopf bis Fuß durchsuchen. Diese Operation ist teuer!

Die Operationen des Stacks wie auch der Queue sind ebenfalls sehr effizient. Die Dequeue bietet jedoch üblicherweise auch Methoden an um auf das \(i\)-te Element in der Liste zuzugreifen. Da wir durch die Liste iterieren müssen, ist die Laufzeit dieser Operation abhängig von der Anzahl der Elemente (size). Folgende Tabelle liefert einen Überblick über die Methoden der Dequeue.

Operation	Laufzeit	Beschreibung
`size`	\(\mathcal{O}(1)\)	Liefert Anzahl der Elemente
`prepend(element)`	\(\mathcal{O}(1)\)	Fügt das Element `element` vorne an (es wird zum Head)
`append(element)`	\(\mathcal{O}(1)\)	Fügt das Element `element` hinten an (es wird zum Tail)
`first()`	\(\mathcal{O}(1)\)	Liefert erstes Element (Head) ohne es zu löschen
`last()`	\(\mathcal{O}(1)\)	Liefert letzte Element (Tail) ohne es zu löschen
`remove_first()`	\(\mathcal{O}(1)\)	Liefert erstes Element (Head) und löscht es aus der Liste
`remove_last()`	\(\mathcal{O}(1)\)	Liefert letzte Element (Tail) und löscht es aus der Liste
`contains(element)`	\(\mathcal{O}(n)\)	`True` genau dann wenn `element` in der Liste ist.
`__getitem__(i)`	\(\mathcal{O}(n)\)	Liefert Element an der `i`-ten Stelle in der Liste
`__setitem__(i, value)`	\(\mathcal{O}(n)\)	Ersetzt `i`-tes Element in der Liste mit `value`
`__delitem__(i)`	\(\mathcal{O}(n)\)	Löscht das `i`-te Element aus der Liste

Es ist hierbei zu beachten, dass wenn wir einen Knoten gegeben hätten, das Löschen dieses Knoten mit einer Laufzeit von \(\mathcal{O}(1)\) realisierbar wäre. Ebenso effizient wäre das Einfügen eines Knotens den wir an einen gegebenen Knoten lediglich anhängen müssten. Die Datenstruktur kapselt jedoch den Zugriff auf diese Knoten.

10.4.5.2. Beispielimplementierung#

Der Folgende Code zeigt die Realisierung eines Knotens durch eine Python-Klasse.

class NodeD:
    def __init__(self, value, predecessor=None, successor=None):
        self.value = value
        self.successor  = successor
        self.predecessor = predecessor
        
    def __repr__(self):
        return repr(self.value)
    
    def append(self, node):
        successor = self.successor
        
        self.successor = node
        node.predecessor = self
        
        node.successor = successor
        if successor:
            successor.predecessor = node
        
    def prepend(self, node):
        predecessor = self.predecessor
        
        self.predecessor = node
        node.successor = self
    
        node.predecessor = predecessor    
        if predecessor:
            predecessor.successor = node

Lassen Sie uns ein paar Knoten verketten. print_nodes gibt die geamte liste aus, sodass wir kontrollieren können was passiert.

a = NodeD('A')
b = NodeD('B')
c = NodeD('C')
d = NodeD('D')
e = NodeD('E')
a.append(b)
b.append(c)
c.append(d)
d.append(e)
print_nodes(a)

['A' <=> 'B' <=> 'C' <=> 'D']

Kennen wir den Knoten (hier c), können wir nach oder vor ihm mit konstanter Laufzeit ein Element einfügen. Dazu müssen wir die richtigen Zeiger verbiegen:

c.append(NodeD('G'))
print_nodes(a)

['A' <=> 'B' <=> 'C' <=> 'G' <=> 'D']

Einen uns bekannten Knoten (hier b) können wir sehr effizient löschen. Dazu müssen wir ebenfalls die richtigen Zeiger verbiegen:

a.successor = c
c.predecessor = a
b.successor = None
b.predecessor = None
print_nodes(a)

['A' <=> 'C' <=> 'G' <=> 'D']

Die Klasse DoubleLinkedList zeigt eine sehr simple Realisierung einer doppelt verketteten Liste. Die Datenstruktur wird durch Knoten realisiert, erlaubt es uns aber nicht direkt auf Knoten zuzugreifen.

Show code cell source Hide code cell source

class DoubleLinkedList:
    def __init__(self):
        self._head = None
        self._tail = None
        self._size = 0
        
    def __repr__(self):
        text = '['
        node = self._head
        for i in range(self._size):
            text += node.__repr__()
            node = node.successor
            if i < self._size-1:
                text += ' <=> '
        text += ']'
        return text
        
    @property
    def size(self):
        return self._size
    
    def first(self):
        return self._head.value
    
    def last(self):
        return self._tail.value
    
    def remove_last(self):
        tail = self._tail
        self._tail = self._tail.predecessor
        tail.predecessor = None
        
        if self._tail:
            self._tail.successor = None
        self._size -= 1
        return tail.value
        
    def remove_first(self):
        head = self._head
        self._head = self._head.successor
        head.successor = None
        
        if self._head:
            self._head.predecessor = None
        self._size -= 1
        return head.value
            
    def append(self, vale):
        node = NodeD(value)
        if self._head:
            self._tail.append(node)
            self._tail = node
        else:
            self._head = node
            self._tail = self._head
        self.size += 1
        
    def prepend(self, value):
        node = NodeD(value)
        if self._head:
            self._head.prepend(node)
            self._head = node
        else:
            self._head = node
            self._tail = self._head
        self._size += 1
        
    def contains(self, value):
        node = self._head
        for _ in range(self.size):
            if node.value == value:
                return True
            node = node.successor
        return False
    
    def __get_node(self, key):
        if key < 0:
            key = key+self.size
        
        if self.size//2 > key:        # forwards
            r = range(key)
            node = self._head
            for _ in range(key):
                node = node.successor
        else:                         # backwards
            node = self._tail
            r = range(self.size-1, -1, -1)
            for _ in range(key):
                node = node.predecessor
        return node
    
    def __delitem__(self, key):
        # del lst[key]
        if key == 0:
            self.remove_first()
        elif key == self.size-1 or key == -1:
            self.remove_last()
        else:
            node = self.__get_node(key)
            predecessor = node.successor
            successor = node.successor
            predecessor.successor = succesor
            successor.predecessor = predecessor
            
            node.successor = None
            node.predecessor = None
            self._size -= 1
    
    def __getitem__(self, key):
        # self[key]
        return self.__get_node(key).value
            

    def __setitem__(self, key, value):
        # self[key] = value
        node = self.__get_node(key)
        node.value = value

lst = DoubleLinkedList()
lst.prepend(13)
lst.prepend(31)
lst.prepend(44)
lst.prepend(54)

lst

[54 <=> 44 <=> 31 <=> 13]

lst.last()

lst.first()

print(lst.contains(13))
print(lst[3])
del lst[3]
print(lst.contains(13))
lst

True
54
False

[54 <=> 44 <=> 31]

while lst.size > 0:
    print(lst.remove_last())

lst

31
44
54

[]

10.4.6. Arrays#

Ein Array ist eine statische Sammlung. Es wird durch einen zusammengesetzen Speicherbereich realisiert. Ein Array beinhaltet üblicherweise Elemente die alle vom gleichen Datentyp sind, oder allesamt Zeiger sind, die alle auf Objekte des selben Datentyps zeigen.

Arrays bieten folgende Operationen.

Operation	Laufzeit	Beschreibung
`size`	\(\mathcal{O}(1)\)	Liefert Anzahl der Elemente
`__getitem__(i)`	\(\mathcal{O}(1)\)	Liefert Element an der `i`-ten Stelle des Arrays
`__setitem__(i, value)`	\(\mathcal{O}(1)\)	Ersetzt `i`-tes Element des Arrays mit `value`

All diese Operationen müssen eine gute Laufzeit haben. Man sagt auch, ihre (Zeit-)Komplexität ist konstant, d.h. von der Anzahl der Elemente (size) unabhängig, oder kurz \(\mathcal{O}(1)\).

Selbstverständlich können wir ein Array erzeugen, welches mehr Elemente aufnehmen kann als es nach der Erstellung beinhaltet. Die „leeren“ Plätze belegen wir dann zum Beispiel mit Pseudowerten.

Folgendes Beispie veranschaulicht das Prinzip. Dabei ist None der Pseudowert. Wir verwenden eine Python-Liste die das Array simuliert.

def print_word(word):
    chars = ''
    for char in word:
        if char:
            chars += char
    print(chars)
    
word = [None, None, 'A','f','f', 'e', None, None]
print_word(word)

Affe

Ein Array funktioniert wie die oben beschriebene Struktur mit zusammengesetzen Speicherbereich, doch verwehrt es uns die Möglichkeit es dynamisch zu vergrößern oder zu verkleinern.

Arrays in Python?

Anders als in den meisten Sprachen, gibt es in Python keine nativen Arrays.

Es gibt sog. Tupel, die einem Array nahekommen, jedoch kann man die Elemente eines Tupels nicht verändern. In anderen Worten Tupel bieten keine __setitem__(i, value)-Methode. Python-Listen sind hingegen dynamische Arrays.

10.4.7. Dynamische Arrays#

Wäre es nicht toll, wenn wir, bezogen auf die Laufzeit, von Arrays und Dequeues das Beste von beiden bekommen könnten? Druch dynamische Arrays versucht man genau dies zu erreichen.

10.4.7.1. Eigenschaften#

Wir hatten gesagt, dass dynamische Sammlungen auf einem fragmentierten Speicherbereich basieren. Das ist jedoch nicht hunderprozent präzise ausgedrückt, denn dynamische Arrays basieren auf einem zusammengesetzten Speicherbreich, der jedoch immer wieder neu im Speicher angelegt wird.

Gehen wir zurück zu unseren Schließfächern. Was würden Sie anders machen, wenn Sie zum einen 10 Schließfächer benötigen, zugleich aber davon ausgehen müssen, dass weitere Schließfächer im laufe der Zeit gebraucht werden? Wahrscheinlich würden Sie mehr als 10 Schließfächer reservieren. Sie würden vielleitcht eine grobe Schätzung abgeben, wie viele Schließfächer denn wahrscheinlich insgesamgt gebraucht werden. Was passiert aber wenn Sie diese Schließfächer über einen langen Zeitraum benötigen und es auch sein kann, dass diese weniger werden? Angenommen jedes Schließfach kostet pro Tag Geld und zugleich kostet das Bewegen der Objekte von einem Schließfach zum anderen ebenfalls einen Betrag. Wie würden Sie dann die Situation handhaben?

Die Dynamik der dynamischen Arrays

Dynamische Arrays vergrößern und verkleinern sich dynamisch obwohl sie durch einem zusammengesetzen Speicherbereich realisiert werden.

Vergrößert sich das Array, so kann es sein, dass alle Werte kopiert werden müssen (siehe zusammengesetzen Speicherbereich). Das heißt, diese Operation wollen wir nicht zu oft durchführen müssen! Gleichzeitig wollen wir aber auch nicht unnötig viel Speicher vorreservieren. Es ist ein Gleichgewicht aus

ungenutztem Speicher und
Anzahl der Kopiervorgänge.

Es wird folgende Strategie implementiert: Ist das Array voll und es soll ein weiteres Element angefügt werden, wird das Array in einen neuen Bereich kopiert der \(r\)-mal so groß ist wie der ursprüngliche Bereich. Ein guter Wert wäre z.B. \(r = 1.5\). Löschen wir hingegen ein Element aus dem Array und es ist weniger als \(1/r\) belegt, dann verringern wir seinen Speicherverbrauch, sodass zu \(1/r\) belegt ist. Mit dieser Strategie verringern sich die durchschnittlichen Kosten für das Kopieren der Elemente auf einen konstanten Wert!

Deshalb bieten dynamische Arrays folgende Operationen.

Operation	Laufzeit	Beschreibung
`size`	\(\mathcal{O}(1)\)	Liefert Anzahl der Elemente
`insert(element, i)`	\(\mathcal{O}(n)\)	Fügt das Element `element` an der `i`-ten Position an
`append(element)`	\(\mathcal{O}(1)\) (Durchschnitt)	Fügt das Element `element` hinten an
`prepend(element)`	\(\mathcal{O}(1)\) (Durchschnitt)	Fügt das Element `element` vorne an
`remove_first()`	\(\mathcal{O}(1)\) (Durchschnitt)	Liefert und löscht erstes Element aus dem dyn. Array
`remove_last()`	\(\mathcal{O}(1)\) (Durchschnitt)	Liefert und löscht letzte Element aus dem dyn. Array
`contains(element)`	\(\mathcal{O}(n)\)	`True` genau dann wenn `element` in im dyn. Array ist.
`__getitem__(i)`	\(\mathcal{O}(1)\)	Liefert Element an der `i`-ten Stelle des dyn. Arrays
`__setitem__(i, value)`	\(\mathcal{O}(1)\)	Ersetzt `i`-tes Element des dyn. Arrays mit `value`
`__delitem__(i)`	\(\mathcal{O}(n)\)	Löscht das `i`-te Element aus dem dyn. Array

Beachten Sie dass das Löschen und Einfügen eines Elements in mitten des dyn. Arrays, d.h. __delitem__(i) und insert(element, i), teuer ist. Ein unbekanntes Element zu suchen, d.h. contains(element), ist ebenfalls teuer. All anderen Operationen müssen eine gute Laufzeit haben. Man sagt auch, ihre (Zeit-)Komplexität ist konstant, d.h. von der Anzahl der Elemente (size) unabhängig, oder kurz \(\mathcal{O}(1)\). Zu beachten ist allerdings, dass es sich bei einigen Operationen um die durchschnittliche Komplexität handelt. In anderen Worten: Es kann passieren, dass eine solche Operation teuer ist, viele Operationen sind jedoch im Durchschnitt sehr effizient.

10.4.7.2. Dequeue vs Stack vs Queue vs dyn. Array#

In dein meisten Fällen wird das dynamische Array der Dequeue vorgezogen, da es theoretisch gesehen in allen Punkten besser oder fast genauso gut abschneidet. Insbesondere dann wenn wir Elemente indexieren wollen oder oft über die gesamte Liste iterieren müssen. Da die Elemente alle nebeneinander im Speicher liegen ist das Iterieren über alle Elemente in der Praxis schneller als bei einer Dequeue.

Wollen wir jedoch lediglich Elemente ganz vorne und ganz hinten in die Liste einfügen, kann die Dequeue zu einer besseren Laufzeit führen, denn bei ihr handelt es sich nicht um den Durchschnitt. Für den Stack und die Queue gilt dies ebenfalls sofern wir Elemente entsprechend Datenstruktur einfügen und herausnehmen wollen.

10.4.7.3. Beispielimplementierung#

Die Python-Liste ist ein dyn. Array.

10.4.8. Hashmaps#

Siehe Namensregister ab Hashing und das Dictionary

TODO

10.4.9. Bäume#

Siehe Sprechen in der Taucherglocke