Chords

Two tones sounding together are usually termed an interval, while three or more tones are called a chord. – George T. Jones

An interval is defined by exactly two notes. Adding at least one note and letting them all sound together makes a chord. Sometimes an interval is also regarded as a chord, i.e. a dyad. For example, the power chord which consists of the root note and the fifth, (as well as possible octaves of those notes) is a famous guitar chord.

Of course, we can also break up a chord into single notes playing what is called an arpeggio. Though, since instances of any given note within the same pitch class may be interpreted as the same note within a chord, it is more precise for the purposes of analysis to speak of distinct pitch classes. Remeber, the pitch class of C is formed by the C of each octave. Furthermore, since three notes are needed to define any common chord, three is often taken as the minimum number of notes that form a definite chord.

Let us listen to all triads of the diatonic and minor scale.

( // triads of the C major scale
Pbind(
  \scale, Scale.major,
  \degree, [0,2,4] + Pseq((0..7), 1)
).play
)

( // triads of the C minor scale
Pbind(
  \scale, Scale.minor,
  \degree, [0,2,4] + Pseq((0..7), 1)
).play
)

The triads of the minor tend to sound more serious.

Triads

The most prominant chords called triads consist of three notes. Finding a harmonic sounding triad can be achieved by adding ever other note in a scale starting from some root, also called base note (if the chord is in root position) - all the chords played above are in root position. In other words, chords are fully defined by the used key and a combination of degrees (scale note positions). If \(d\) is the degree of the first note then the degree sequence

\[(d, d+2, d+4)\]

constitute all natural triads within a scale. For example, for a major scale in the key of C (all white key on a piano),

\[(\text{E, G, B})\]

constitutes the iii-minor chord within this key.

Similar to diatonic scale where notes are numbered from one to seven, we also use roman numerals (I, ii, iii, IV, V, vi, vii) to denote the position of the chord’s root with respect to the key we are in. In C we have C-D-E-F-G-A-B, therefore, E-G-B is numbered by iii and it is a minor chrod since E-G is a minor third interval and not a major third interval like G-B, see section Intervals.

We use capitalized roman numerals if we refer to a major chord, otherwise we use lowercase numerals. The numbers translate to the degrees of the key. In the following first table I use the major scale in the key of A:

A Major	I	ii	iii	IV	V	vi	vii
Name	Tonic	Supertonic	Mediant	Subdominant	Dominant	Submediant	Leading note
Quality	Major	Minor	Minor	Major	Major	Minor	Diminished
Intervals	4,3	3,4	3,4	4,3	4,3	3,4	3,3
Root	A	B	C#	D	E	F#	G#

In the second table I use the minor scale in the key of A:

A Minor	i	ii\(^\circ\)	III	iv	v	VI	VII
Name	Tonic	Supertonic	Mediant	Subdominant	Dominant	Submediant	Leading note
Quality	Minor	Diminished	Major	Minor	Minor	Major	Major
Intervals	3,4	3,3	4,3	3,4	3,4	4,3	4,3
Root	A	B	C	D	E	F	G

Each triad of a scale has a more or less defined role. I/i act as the tonic, i.e, the home or the tonal center. Leading tones (vii/VII) lead into the tonic and (iv/IV/V/v) open up possibilities that wants to be resolved into the tonic.

Following the formula, we call (B, D, F#) the B minor chord and (D, F, A) the D major chord, regardless of the scale we are using because the interval B-D is a minor third and from D-F it is a major third. However, we need the scale to determine the tonal role of each chord (and note) within a composition.

Note that all triads within a key are unique and that all major and minor chords contain a perfect fifth. A major chord is defined an interval sequence (4,3) (in semitones) and a minor chord is defined by an interval sequence (3,4). The deminished is defined by (3,3), it contains a diminished fifths / tritone instead of a peferfect fifths. If the interval is (4,4) the chord is augmented.

If we look at all resulting intervals for the major and minor chord we get: 3 semitones (minor third), 4 semitones major third and 7 semitones (perfect fifth). In frequencies of an equally tempered octave this equates to

\[\begin{equation*} \begin{split} 2^{3/12} &\approx 1.189 \approx 1.19, \quad \text{minor third}\\ 2^{4/12} &\approx 1.259 \approx 1.26, \quad \text{major third}\\ 2^{7/12} &\approx 1.498 \approx 1.50, \quad \text{perfect fifth.} \end{split} \end{equation*}\]

All these ratios are relatively simple; thus, the tone is consonant.

For the diminished chord, we get two intervals of 3 semitones (minor third) and an interval of 6 semitones (minor seventh) which is regarded as very dissonant. In frequencies of an equally tempered octave this equates to

\[\begin{equation*} \begin{split} 2^{3/12} &\approx 1.1890 \approx 1.19, \quad \text{minor third}\\ 2^{6/12} &\approx 1.4142 \approx 1.41, \quad \text{tritone.} \end{split} \end{equation*}\]

Note that we can categorize the chord into major, minor, or diminished solely by the interval sequence. A chord in root position is fully defined by interval sequence and its first note, called root. Consequently, we do not have to know the key. We can name the chord by its root and the interval sequence, e.g., B minor chord (Bm) is equal to (B, D, F#). Musicians use only the note symbol, such as F, to denote the major chord of that note, e.g., F major chord. This can be confusing because scales and keys are denoted similarily.

Inversion

Changing the order of the notes within a chord by changing their octaves is called inversion. Since the lowest note within a chord is important with respect to the tonality of the chord, moving the second note down is called first inversion while making the third note the bass note is called second inversion. Of course, we can also move the root up instead.

Because of the asymetric propertie of major and minor scales, inversion changes the quality of the chord! For example, E-G-B is Em, i.e. a (3, 4) semitones interval which is a minor third and a major third. Its first inversion G-B-E results in a (4, 5) semitones interval which is a major third and a minor sixth.

Its second inversion B-E-G results in (5, 3) which is a minor sixth and a minor third. The following staff notation shows three chords from left to right: E-G-B in root position, first inversion and second inversion.

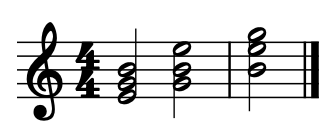
Tonality

By relating chords via a chord progression they can have different types of emotional effects across a piece of music.