Amplitude

In the description of the UGen called Amplitude we find the following statement:

Tracks the peak amplitude of a signal.

I had a hard time to understand what is going on here, especially how one should deal with the arguments attackTime and releaseTime. Why is this UGen even helpful? Isn’t the amplitude of a signal \(y(t)\) defined by \(|y(t)|\)?

Well THE amplitude is not clearly defined at all. Instead we are dealing with different kinds of amplitudes. For example, we say that the following signal

({
    var freg = 400;
    var attackTime = 0.1;
    var releaseTime = 0.2;
    var env = EnvGen.ar(Env.perc(attackTime: attackTime, releaseTime: releaseTime));
    var sig = SinOsc.ar(freg) * env;
    sig
}.plot(0.4);
)

has an amplitude of 1.0.

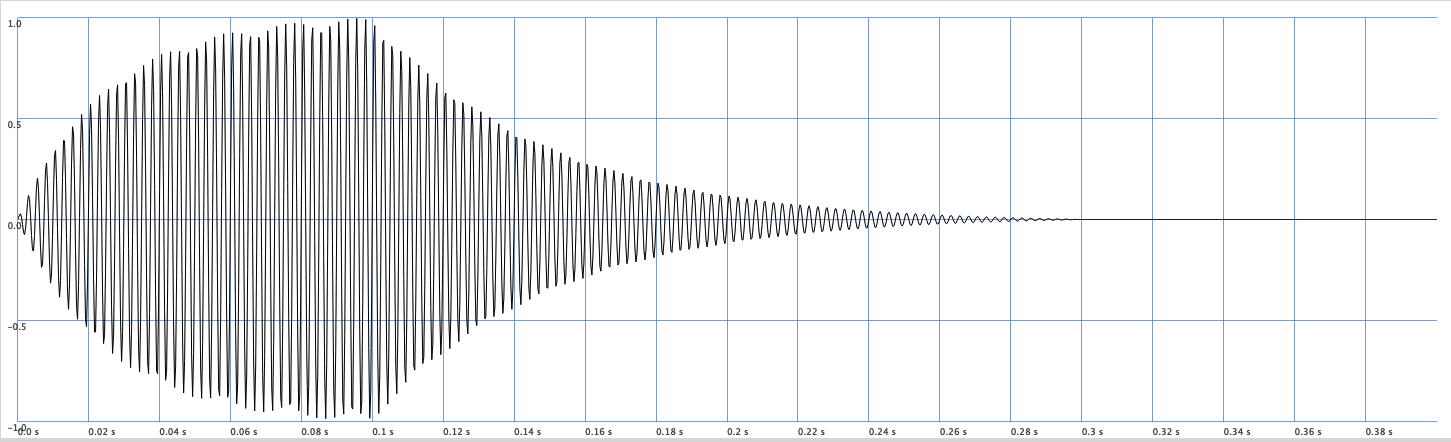
Fig. 11 A modulated amplitude of a sine wave. We say that this signal has an amplitude of 1.0.

What we actually mean is the maximum amplitude of the signal:

(1)\[\begin{equation} \max\limits_{t \in ]-\infty; +\infty[ } |y(t)|. \end{equation}\]

Ok, but there is more. What about the perceived amplitude of a signal. In the example above, we can perceive that the sound gets louder over a time of 0.1 seconds and decays away in 0.2 seconds.

For an increasing and decaying signal we could compute each local maxima and minima, take the absolute value and interpolate in between. That is basically what Amplitude does. It computes the perceive loudness, i.e., local amplitude of a signal!

The following code generates another plot, that shows the difference.

({
    var freg = 400;
    var attackTime = 0.1;
    var releaseTime = 0.2;
    var env = EnvGen.ar(Env.perc(attackTime: attackTime, releaseTime: releaseTime));
    var sig = SinOsc.ar(freg) * env;
    [Amplitude.ar(sig, attackTime: attackTime, releaseTime: attackTime), sig, abs(sig)]
}.plot(0.4);
)

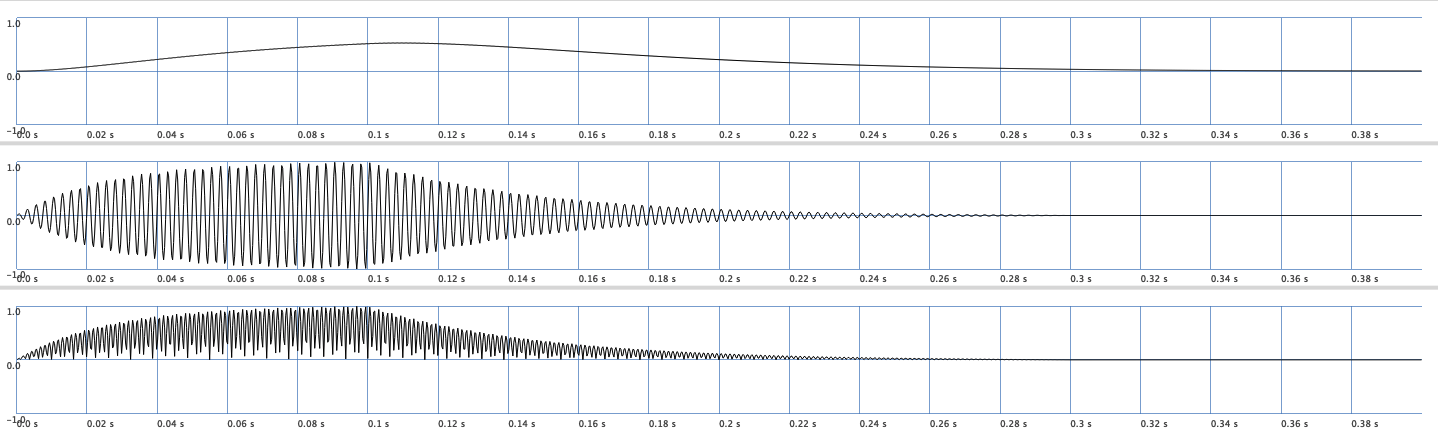
Fig. 12 A modulated amplitude of a sine wave. At the top the measured perceive loudness using Amplitude. In the middle the actual signal \(y(t)\) and at the bottom \(|y(t)|\).

Somehow Amplitude underestimates the perceive loudness quite a bit.

Futhermore, we have to tell Amplitude the time period the signal loudness increases attackTime and the time period the amplitude decreases releaseTime. If we don’t know these values or we are looking at a signal without an envelope, we have to choose a decently short time periods. Amplitude seems to analyse each chunk of the signal of size attackTime + releaseTime and computes an amplitude value for this time period. Therefore, if we choose attackTime + releaseTime \(\approx 1/(c \cdot f)\), where \(f\) is the frequency of the signal and \(c > 1\), we almost get \(|y(t)|\). I conclude that these values should be greater than \(1/f\).

Note that we are talking about a discrete signal even if we write \(y(t)\).

The default values are attackTime: 0.01 and releaseTime: 0.01, so for a signal with a frequency close to \(100\) Hz, we should increase these values.

Let’s end with an example. Here we cut the noisy sound if its amplitude measured by Amplitude is below 0.2.

({ 
    var sig = WhiteNoise.ar(0.5!2) * 0.5 * SinOsc.kr(1);
    sig * (Amplitude.ar(sig) > 0.2);
}.play
)

As longas Amplitude.ar(sig) > 0.2 is true, it returns (on the server-side) not true but 1. Otherwise the expression is evaluated to 0.