Subtractive Synthesis and Filters#
In additive synthesis, we begin with silence and progressively combine more straightforward waveforms to achieve a complex sound. Subtractive synthesis operates in the opposite way. We start with a rich, complex signal, such as white noise, and apply filters to decrease, eliminate, or even amplify the amplitude of certain frequency bands. Therefore, when discussing subtractive synthesis, it is imperative to talk about filters!
Any medium through which the music signal passes, whatever its form, can be regarded as a filter. However, we do not usually think of something as a filter unless it can modify the sound in some way. For example, speaker wire is not considered a filter, but the speaker is (unfortunately). – Julius O. Smith
A digital filter simply refers to a filter that operates on digital signals, such as sound represented within a computer. Due to our conventional interpretation of the term filter, our basic understanding might suggest that filters primarily diminish parts of the signal – but this is not the entire story. With respect to the frequency domain, filters have a
amplitude frequency response, and
phase response.
A filter that drastically reduces a specific range of frequencies to zero, leaving the rest unaffected, is termed a brick wall. For instance, we could calculate the Fourier transform of a signal and then multiply the frequencies within that range by zero. However, due to computational complexity and buffering constraints, such ideal filters prove to be rather impractical for real-time use. Consequently, most filters operate differently, working to either reduce or amplify the intensity of specific frequencies.
Filtering and the Fourier transform
Filtering can be achieved by multiplication in the spectural domain and by convolution in the time domain.
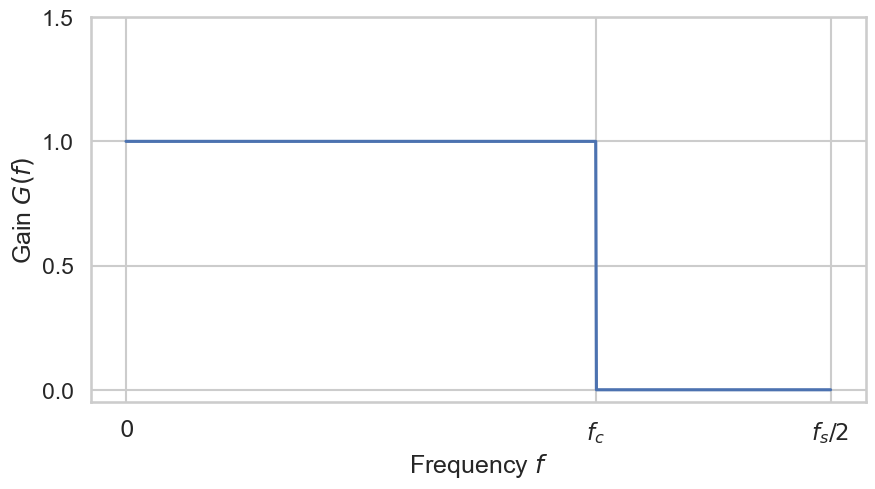
For instance, if we aim to entirely filter out all high frequencies up to a cutoff frequency \(f_c\), without affecting the low frequencies \((f \leq f_c)\), our ideal brick wall filter would exhibit an amplitude frequency response resembling the plot shown below.
Such ideal filter is the simplest lowpass filter. The gain is 1 in the passband, which pans frequencies from 0 Hz to the cutoff frequency \(f_c\) Hz, and its gain is 0 in the stopband (all frequencies above \(f_c\)). The output spectrum is obtained by multiplying the input spectrum by the amplitude response of the filter.
Apart from changing the level of specific frequencies, filters often change the phase of the signal, e.g., \(\sin(2\pi t)\) is transformed to \(\sin(2\pi t + 0.5\pi)\). Some filters do primarily apply such period shifts and we might not think of them as filters. For example, the allpass filter passes all frequencies untouched but attunes phases.
Lowpass filters are used everywhere because they can smoothen the harshness of a sound.
A lot of filters support feedback, i.e., the output signal of the filter goes back into it. Each time the signal is fed back, its level gets reduced such that the feedback eventually comes to an end. Such feedback can be used to synthesis reverberation.
In combination with an impulse (e.g. Impuse) filters can be used to contruct surprising effects.
And with ressonance, filters can add many aspects to the timbre of a sound.
SuperCollider offers a large variety of filters. Execute
Filter.dumpClassSubtree;
to print a list of all filters to the post window.
In summary, filters and substractive synthesis are inseperable.
We can use static filters to emphasize specific frequencies.
We can use static filters to create formants in a sound and imitate the characteristics of the human voice or traditional acoustic instruments.
A resonance filter with a moderate resonance bandwidth with a cutoff frequency that tracks the pitch can create a characteristic quality that remains tonally consistent as we play the keyboard.
For some resonance filters, if we decrease the resonance bandwidth, we enter an area where the filter is at the brick of self-oscillation. This creates a distinctive distortion that can be a perfect starting point.
If we decrease the resonance bandwidth even further, the filter will become a sine wave generator in its own right. In theory, no input signal is passed at this point, but few filters altogether remove all the signal, and the result is a tortured sound that has extensive uses in modern music.
In analog synthesis, filters are the defining element of a synthesizer. They are also crucial in digital synthesis, and if you are into creative synthesis, your sound generation will depend upon what you have and what you do with it.