Frequency Filters

When we talk about filters, we usually mean frequency filters. Their arguments are more meaningful than the filters discussed in section Basic Filters. They attune the band of frequencies of a signal.

As Butterworth stated:

An ideal electrical filter should not only completely reject the unwanted frequencies but should also have uniform sensitivity for the wanted frequencies. – Stephen Butterworth

Such an ideal filter cannot be achieved but one can try to get close approximations by increasing the number of filter elements. In practice, a frequency filter decreases the power/gain of high frequncies.

Lowpass Filter

A lowpass filter filters frequency above its cutoff frequency. It could also be called highfrequency filter. Lowpass filters are used to attenuate high harmonics and make sound darker or smoother in timbre. A lowpass filter is often combined with a resonant because (with the respective cutoff frequency) lowpass filters leave the fundamentals of the signal intact. So they do not usually affect the perceived and subjective pitch.

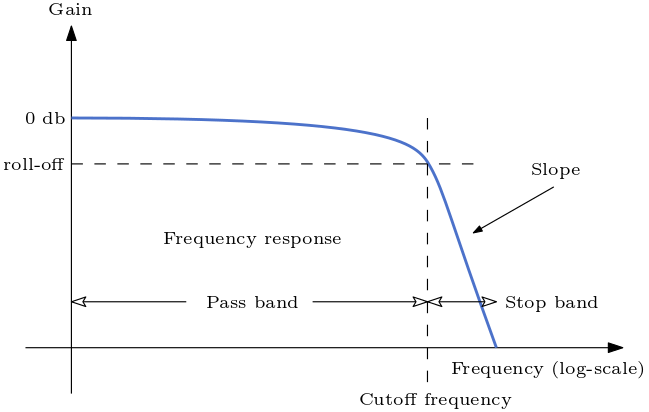
Fig. 51 The gain over frequency of a signal filtered by a lowpass filter.

In nature, low frequencies tend to die out much slower than high frequencies. This makes sense intuitively because it requires more power to keep the vibration of, for example, a string high.

With LPF sclang offers a second-order Butterworth lowpass filter. Compared to a first-order low pass filter, a second-order low pass filter has two stages. In principle, the gain in amplitude over frequencies has a steeper slope.

Second-order Butterworth Lowpass Filter

A second-order Butterworth lowpass filter has a slope of -12 db per octave.

Let us compare a sawtooth wave with a filtered sawtooth wave where the cutoff frequency is equal to the fundamental of the sawtooth:

{Saw.ar(440)*0.25}.play

{LPF.ar(Saw.ar(440)*0.25, MouseX.kr(40, 2000))}.play

Let us also have a look at how the waveform changes if we reduce the cutoff frequency over time.

// reduce the cutoff frequency from 2*freq to 0 over the time span of 10 cycles of the waveform
(
var freq = 440, amp = 0.25;
{	
    var sig = Saw.ar(440)*amp;
    [sig, LPF.ar(sig, Line.ar(2*freq, 0, freq.reciprocal * 10))]
}.plot(freq.reciprocal * 10)
)

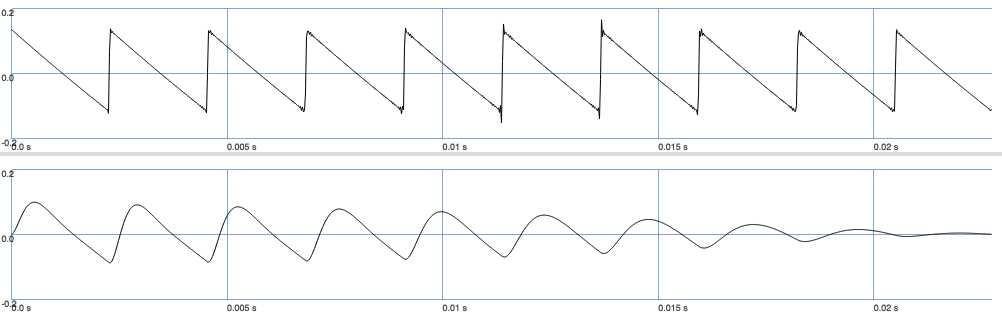
Fig. 52 A sawtooth wave (top) filtered by a modulated lowpass filter (bottom).

We can observer that the maximum amplitude of the filtered signal decreases with the cutoff frequency.

Highpass Filter

A highpass filter filters frequency below its cutoff frequency. Highpass filters are excellent to clean up woofy signals and tighten up arrangements. They can make the sound more clear which can be especially useful for your lead instrument.

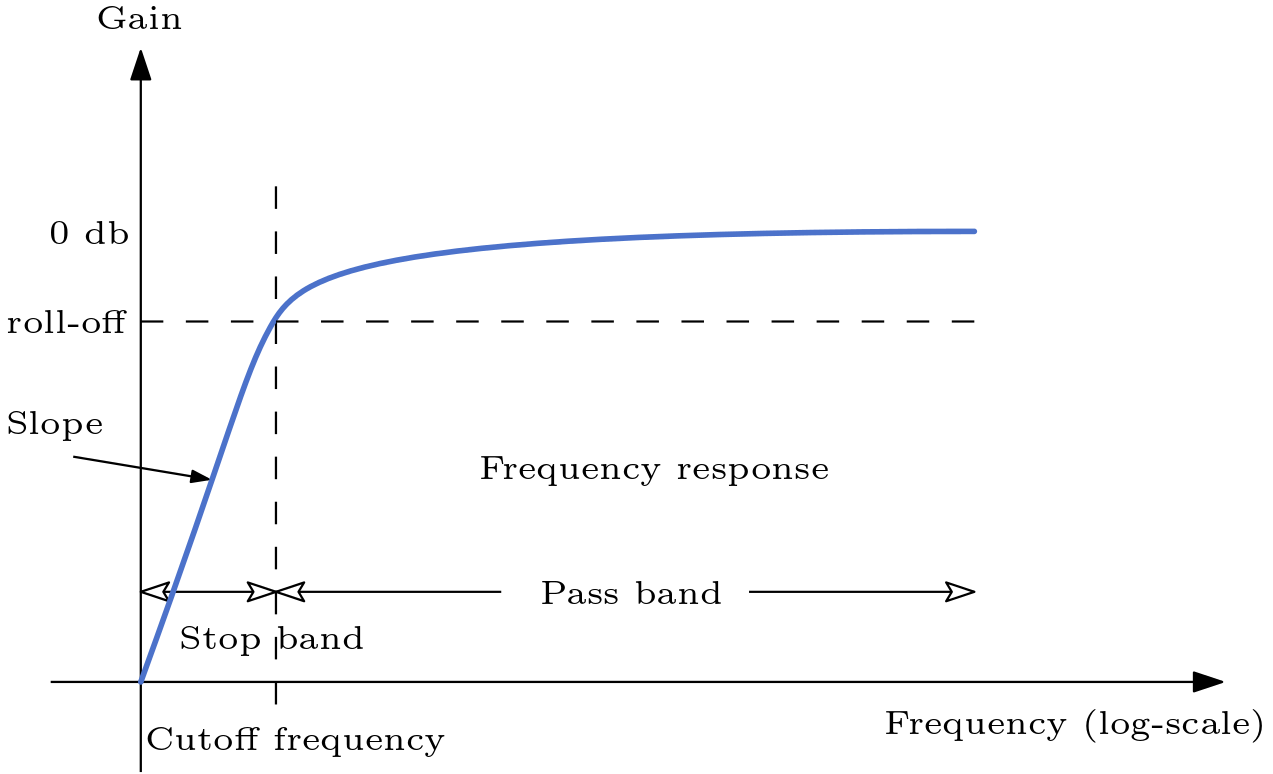
Fig. 53 The gain over frequency of a signal filtered by a highpass filter.

The effect is less obvious, at least with my headphones.

{HPF.ar(Saw.ar(440)*0.25, MouseX.kr(40, 5000))}.play

If we look at a plot using a modulated highpass filter (here we increase the the cutoff frequency over time), we observe that the sawtooth wave becomes sharper.

(
var freq = 440, amp = 0.25;
{	
    var sig = Saw.ar(440)*amp;
    [sig, HPF.ar(sig, Line.ar(0, 2*freq, freq.reciprocal * 10))]
}.plot(freq.reciprocal * 10)
)

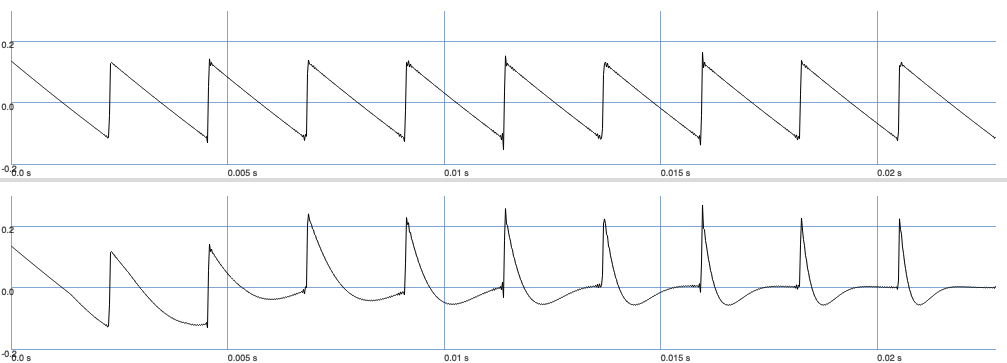
Fig. 54 A sawtooth wave (top) filtered by a modulated highpass filter (bottom).

Bandpass Filter

A bandpass filter filters frequency outside of its band defined by its center frequency and bandwidth. It is a combination of a lowpass and highpass filter.

Combining filters

Combining a lowpass and a highpass filter will not necessarily achieve the same effect because they both apply a phase shift.

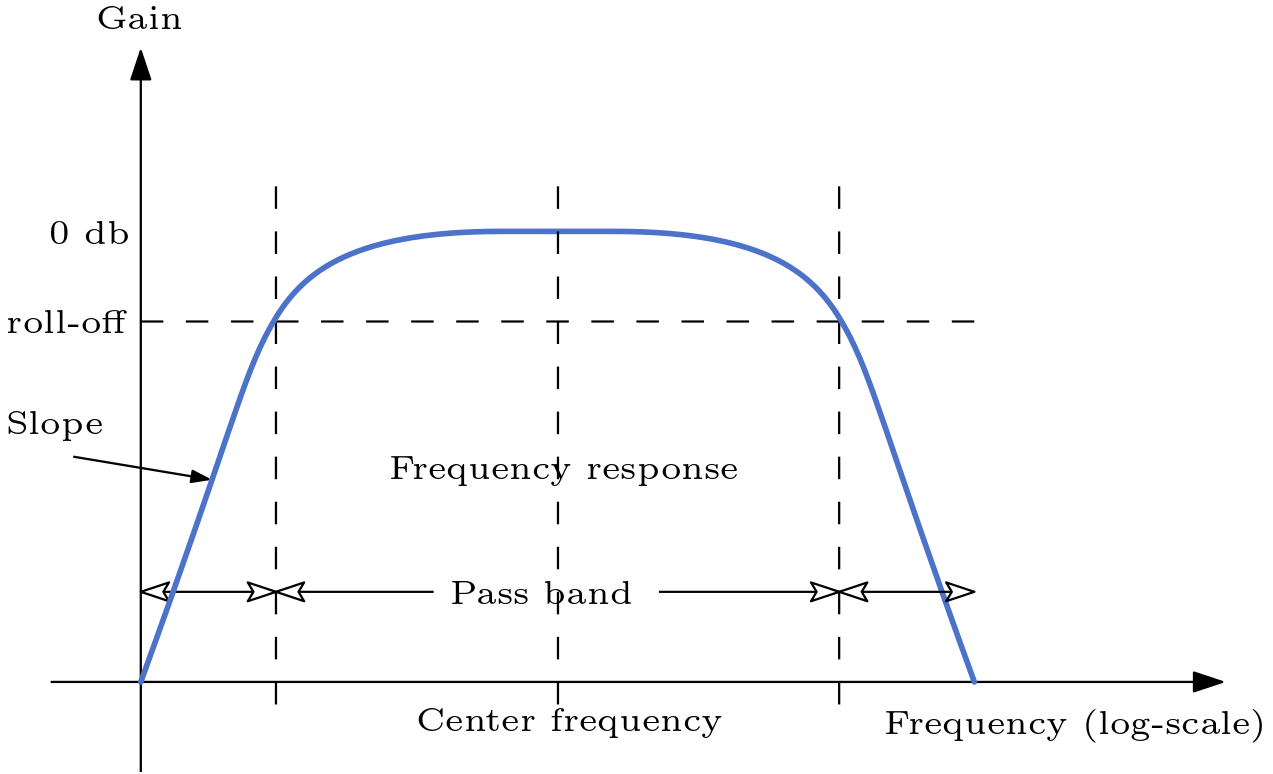
Fig. 55 The gain over frequency of a signal filtered by a bandpass filter.

sclang offers us the UGen called BPF. It is a second-order Butterworth bandpass filter. Instead of defining the bandwith, we define rq which is equal to bandwidth / center frequency thus bandwidth = rq * center frequency.

Let us plot the effect of a modulated bandpass filter. Here we only change the center frequency from 220 Hz to 880 Hz.

(
var freq = 440, amp = 0.25, bandwidth = 200;
{	
    var sig = Saw.ar(440)*amp;
    var centerFreq = Line.ar(0.5*freq, 2*freq, freq.reciprocal * 10);
    [sig, BPF.ar(sig, centerFreq, bandwidth/centerFreq)]
}.plot(freq.reciprocal * 10)
)

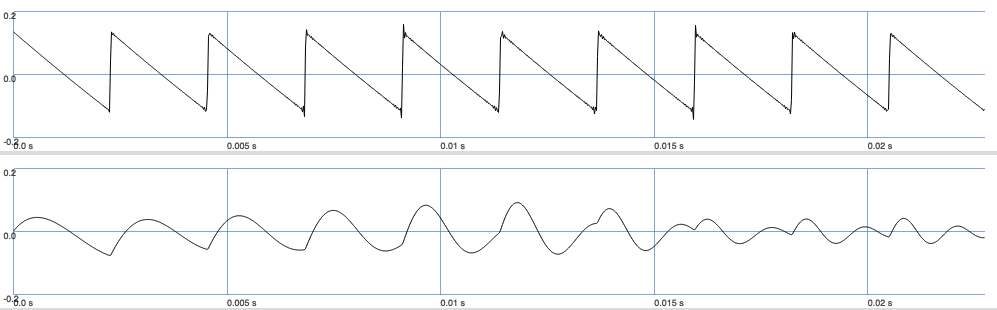
Fig. 56 A sawtooth wave (top) filtered by a modulated bandpass filter (bottom).

Let’s have a listen:

{BPF.ar(Saw.ar(440)*0.25, MouseX.kr(40, 2000), MouseY.kr(2.0, 0.01))}.play