Fundamental Waveforms#

Jean-Baptise Joseph Fourier discovered that every function that is

  1. periodic,

  2. piecewise continuous and

  3. bounded

can be represented as a Fourier series, see section Fourier Series. In theory, the Fourier series of a function consists possibly infinite many terms and since our hardware resources are finite, we can only generate an approximation of the real thing.

Furthermore, the Fourier series is a sum of sine and cosine waves where the frequency of each wave in the sum is an integer multiple of the fundamental frequency! We call these waves harmonic overtones or just harmonics. The more harmonic overtones are present, the richer the sound.

Frequencies that are present which are not integer multiple of the fundamental are inharmonic overtones or just inharmonics. If there are many harmonics and only a few inharmonics present, we can clearly perceive a pitch, and we call the sound harmonic. If it is the other way around, there is no longer a pitch and we call the sound inharmonic. Drums and bells have an inharmonic sound while the piano, a guitar and strings have a harmonic sound. The timbre of a sound is determined by the power distribution within the overtones of the sound, i.e. who ‘’much’’ a certain frequency above the fundamental is present.

To understand the sound of a specific signal it is very usful to look at the amount of harmonic and inharmonic overtones. The Fourier transform and especially the discrete Fourier transform can help us with if we want to analyse a given signal.

Using the Fourier transform, one can extend the concept of the Fourier series to non-peridic functions. I call functions with these properties, including non-periodic ones, signals. Functions that describe an amplitude \(y(t)\) over the time \(t\) are audio signals and have these qualities.

To better understand a signal, it is essential to understand its Fourier series. Often we cut a long signal into small chunks and compute the discrete Fourier transform for those chunks. Therefore, the representation of the function in the frequency domain changes over time. In fact, the stethoscope displays the frequencies of the functions that are the components of the short time Fourier transform.

In additive synthesis, we construct a signal by combining harmonic and inharmonic overtones. Therefore, we are in complete control of how harmonic or inharmonic our result will be. But we do not have to combine only single harmonics. We can use wave forms that already consist of certain harmonics (or inharmonics).

In general, for audio synthesis, there are some fundamental oscillators. Both types of synthesizers, that is, analog as well as digital synthesizers, offer these basic oscillators as a starting point. Espacially, in additive synthesis we really wanna understand the effect of each basic oscillator. So let us try to understand their timbre by looking at the coefficient of their Fourier series, i.e. the power distribution within their harmonics.

The Sine Wave#

The sine wave

(48)#\[\begin{split} \begin{split} y_\text{sine}(t) &= A \cdot \sin(2\pi \cdot f \cdot t)\\ &= A \cdot \frac{e^{i 2\pi \cdot f \cdot t} - e^{-i 2\pi \cdot f \cdot t}}{2i}\\ &= A \cdot \mathbf{Re}\left( -i \cdot e^{i2\pi \cdot f \cdot t} \right)\\ &= A \cdot \mathbf{Im}\left(e^{i2\pi \cdot f \cdot t} \right) \end{split}\end{split}\]

is the most pure, most basic, and most simple signal. The sine or cosine wave is the most basic waveform there is. Its Fourier series is equivalent to Eq. (48). Note that I also use the exponetial form introduced in section Complex Numbers but don not worry, it is not that important here. The sine or cosine wave, consists of only the fundamental frequency \(f\) and is theoretically the basis for all other signals. Sine is equals to cosine shifted by \(\pi/2\).

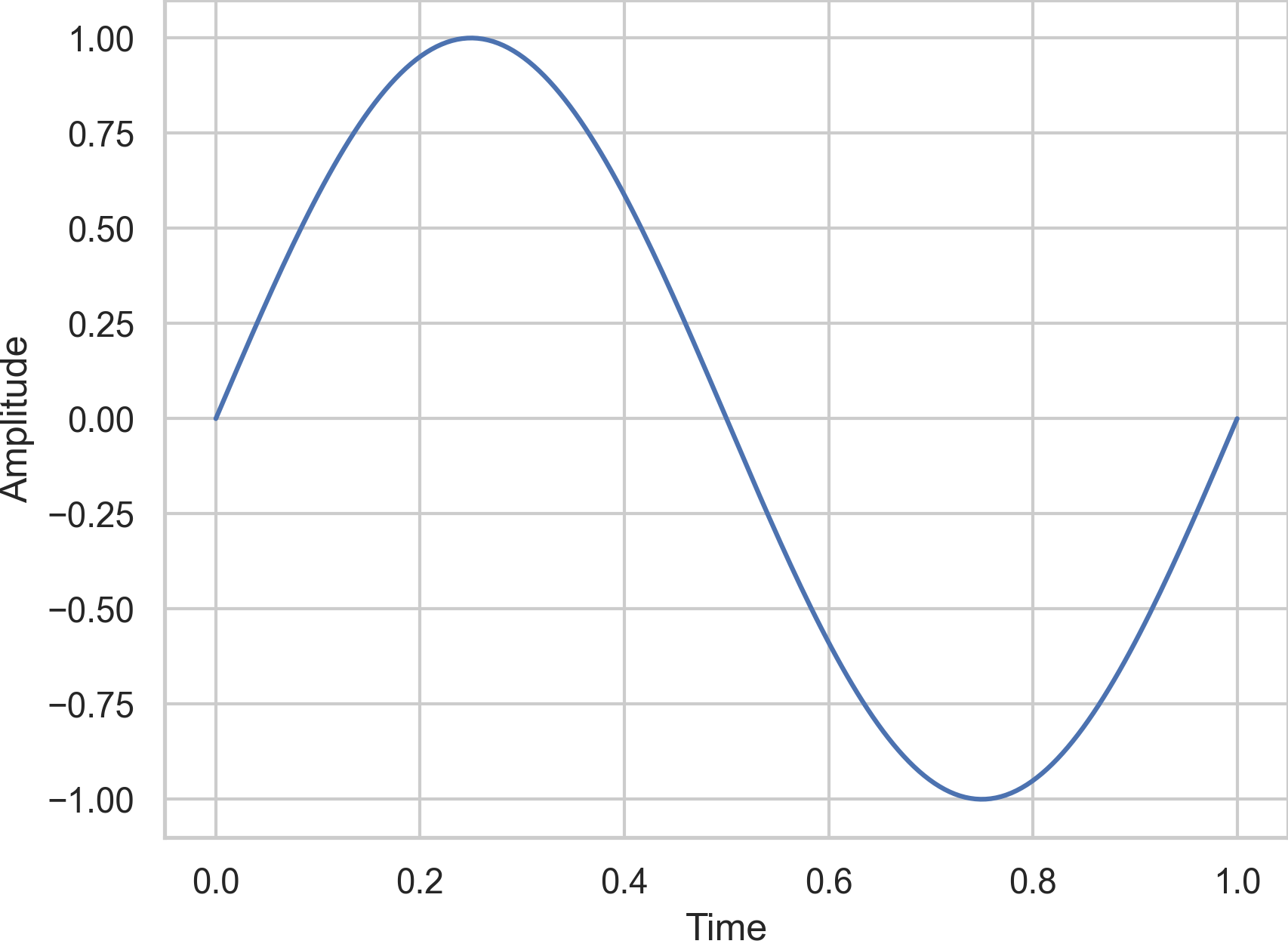
../../../_images/sine.png

Fig. 38 The sine wave with a frequency and amplitude of 1.#

A sine wave is purely harmonic but it has no overtones. Therefore, it sounds rather smoth and soft. It can be used to generate a nice bass or to amplify the sound of a drum or one can use it as a subbase. It can also be used to add a certain harmonic to a sound.

{SinOsc.ar(220!2)*0.25}.play;

The Sawtooth Wave#

The first more complicated and important waveform I want to discuss is the so-called sawtooth wave

(49)#\[ y_\text{saw}(t) = A \cdot 2 \left( f \cdot t - \left \lfloor{ \frac{1}{2} + f \cdot t} \right \rfloor \right),\]

where \(A\) is the amplitude and \(f\) is the frequency of the wave. The problem with implementing Eq. (49) directly is that infinitely high frequencies are present and in the digital world frequencies above halfe the Nyquist frequency are projected back into lower most certainly inharmonic frequencies, see section Sampling. The unit generator LFSaw is such a non-band-limited sawtooth wave. LF stands for low frequency. Saw is a band-limited sawtooth generator which can be used for high frequencies.

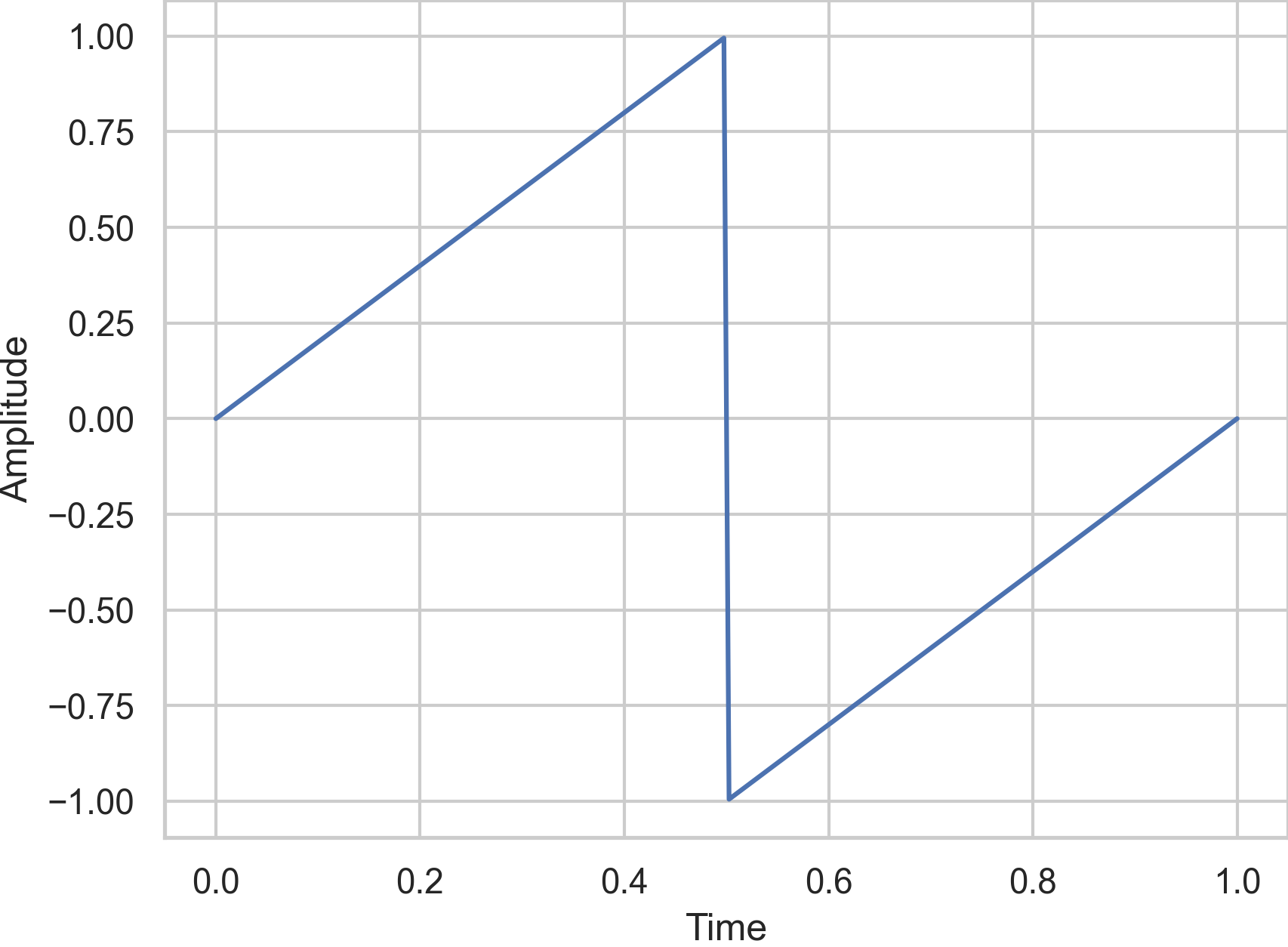
../../../_images/sawtooth.png

Fig. 39 The non-band-limited sawtooth wave with a frequency and amplitude of 1.#

I generated this plot using Python but we can do the same in sclang. However, the \(x\)-axis will be always the number of the sample. Let us generate the plot in Fig. 39 using sclang:

(
var trifunc = {
    arg t;
    var freq = 1, amp;
    amp = (freq*t - floor(1/2 + (freq*t)));
};

var t = Array.interpolation(100, 0, 1);
var y = t.collect({arg t; trifunc.value(t);});

y.plot();
)

To understand the sawtooth wave musically, we have to look at its Fourier series:

(50)#\[ y_\text{saw}(t) = A \left( \frac{1}{2} - \frac{1}{\pi} \sum_{k=1}^{\infty} (-1)^k \frac{\sin(2\pi k f t)}{k} \right).\]

We can approximate the series by only summing up the first \(n\) terms:

(51)#\[ y_{\text{saw},n}(t) = A \left( \frac{1}{2} - \frac{1}{\pi} \sum_{k=1}^{n} (-1)^k \frac{\sin(2\pi k f t)}{k} \right).\]
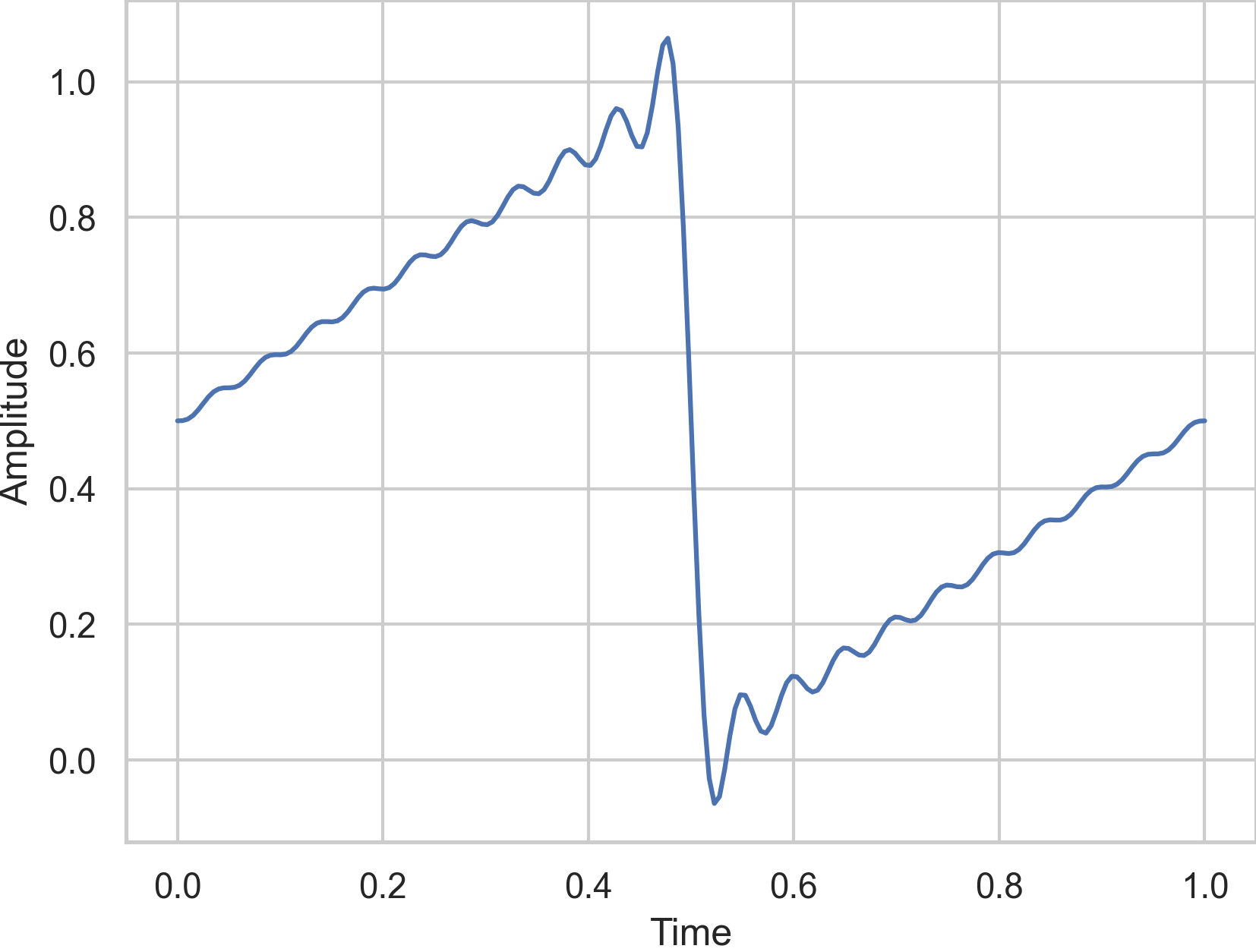
../../../_images/sawtooth_20.png

Fig. 40 An approximation for the Fourier series of the sawtooth wave with a frequency and amplitude of 1 using \(n=20\).#

The evaluation of many sine functions is computational more expensive than evaluating Eq. (49). However, we learn from Eq. (50) that

  1. each harmonic of \(k \cdot f\) with \(k \in \mathbb{N}\) of the fundamental \(f\) is present and

  2. the amplitude of the harmonic \(k\) decrease by \(1/k\).

We can compute an approximation of the sawtooth wave by the technique of additive synthesis using Eq. (51).

Even if the sawtooth wave does not quite sound like a string instrument, its properties are similar to the audio signal generated by string instruments. Therefore, the sawtooth wave can be the starting point for modeling the sound of a violin, piano or guitar. Apart from noise, the sawtooth wave is the richest sound produced by any basic oscillator. Its sound is very harmonic since all harmonics are basically present. In general, the sawtooth wave is a good candidate to start with if you want to create a rich harmonic sound or if you want to apply subtractive synthesis.

In sclang we can generate the sound of a sawtooth wave using the unit generator Saw:

{Saw.ar(220!2)*0.25}.play;

The Square Wave#

Another important waveform is the square wave which is a special case of the pulse wave:

(52)#\[ y_\text{square}(t) = A \cdot \text{sign}\left( \sin\left( 2\pi \cdot f \cdot t \right) \right)\]

where \(\text{sign}(\cdot)\) is defined by

(53)#\[\begin{split} \text{sign}(x) = \begin{cases} +1 & \text{ if } x \geq 0\\ -1 & \text{ else.} \end{cases}\end{split}\]
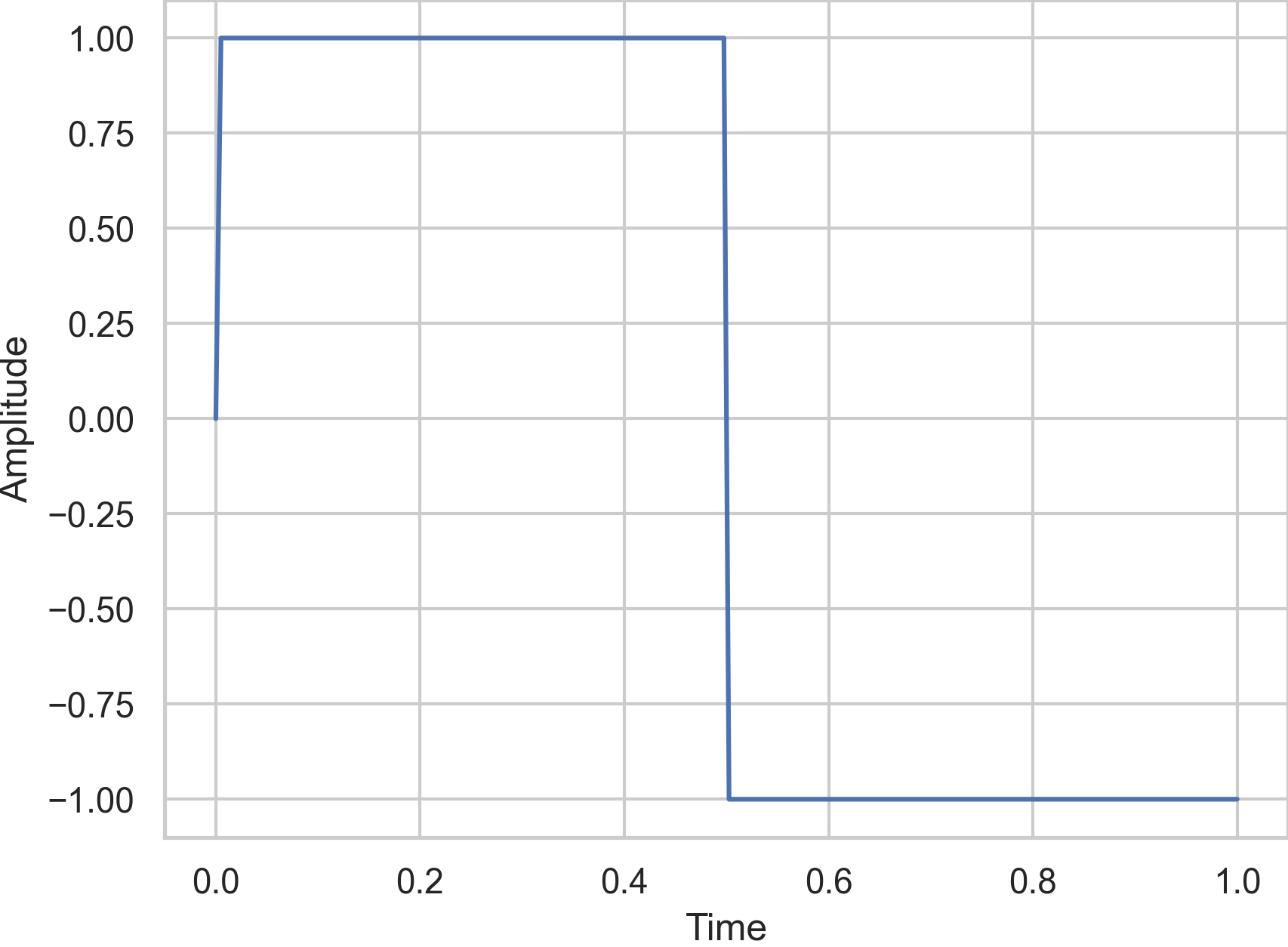
../../../_images/square.png

Fig. 41 The square wave with a frequency and amplitude of 1.#

Let’s look at its Fourier series:

(54)#\[ y_\text{square}(t) = A \cdot \frac{4}{\pi} \cdot \sum_{k=1}^{\infty} \frac{\sin( 2\pi \left[ 2k-1 \right] \cdot f \cdot t)}{2k - 1}\]

Again we learn from the Fourier series Eq. (54) that

  1. each odd harmonic \((2k-1)f\) with \(k \in \mathbb{N}\) of the fundamental \(f\) is present and

  2. the amplitude of the harmonic \(2k - 1\) decreases with \(4/(2k - 1)\)

The amplitudes also decrease linearly with increasing frequencies.

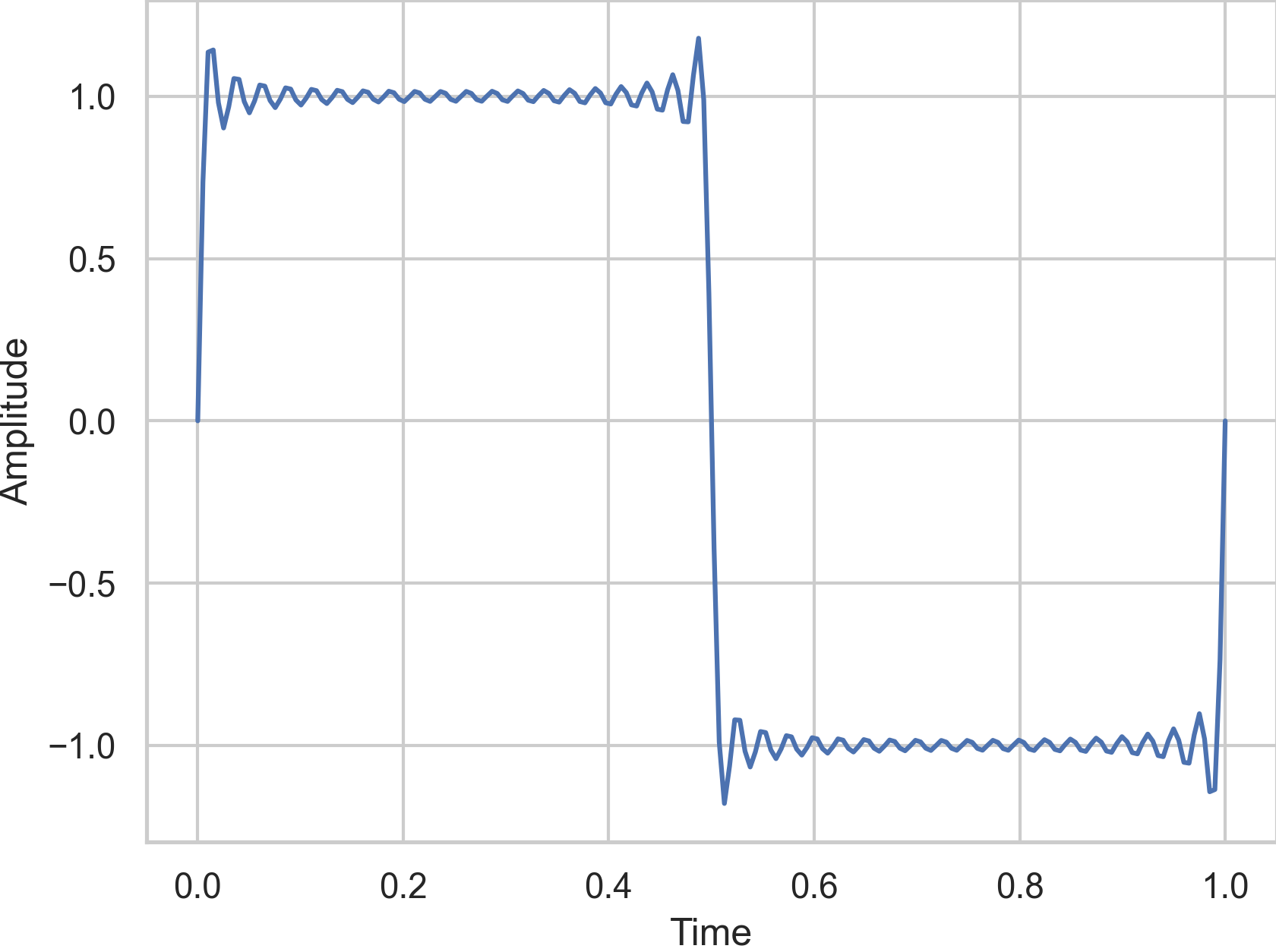
../../../_images/square_20.png

Fig. 42 An approximation for the Fourier series of the square wave with a frequency and amplitude of 1 using \(n=20\).#

The square wave has more harmonics as the sine wave but less than the sawtooth wave. Without any additions, it sounds rather hollow but also rich. It resembles the sound of old video games. The square wave comes often with a special parameter to control its width. The more asymetric the wave, the more metallic and nasal the sound.

The signal of some wind instruments, like the clarinet, is similar to square wave. Their sound contains mostly odd harmonics.

In sclang we can generate the sound of a square wave using the unit generator Pulse:

{Pulse.ar(220!2) * 0.25;}.play;

SuperCollider provides two versions of a square wave: Pulse a band-limited version and a non-band-limited version LFPulse.

The Triangle Wave#

The next important wave is the triangle wave:

(55)#\[ y_\text{tri}(t) = A \cdot \left( 4 \cdot \left| f \cdot (t+1/4) - \left \lfloor{ \frac{1}{2} + f \cdot (t+1/4)} \right \rfloor \right| - 1 \right),\]

where \(\left| \cdot \right|\) is defined by

(56)#\[\begin{split} \left| x \right| = \begin{cases} +x & \text{ if } x \geq 0\\ -x & \text{ else.} \end{cases}\end{split}\]
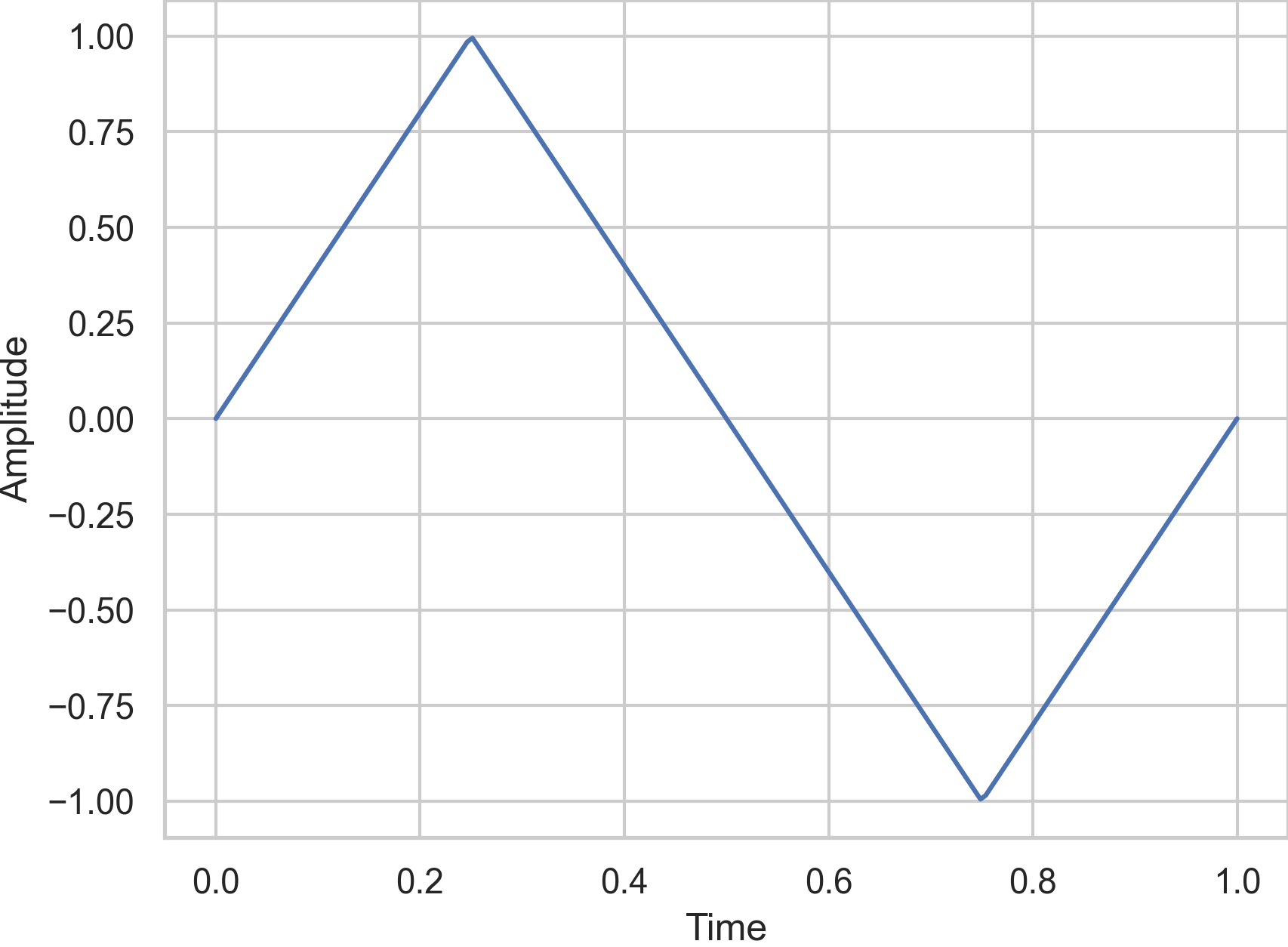
../../../_images/triangle.png

Fig. 43 The triangle wave with a frequency and amplitude of 1.#

Let’s look at its Fourier series:

(57)#\[ y_\text{tri}(t) = A \cdot \frac{8}{\pi^2} \cdot \sum_{k=0}^{\infty} (-1)^k \frac{\sin(2\pi \cdot f \cdot (2k+1) \cdot t)}{(2k+1)^2}\]

Again we learn from the Fourier series Eq. (57) that

  1. each odd harmonic \((2k+1)f\) with \(k \in \mathbb{N}_0\) of the fundamental \(f\) is present and

  2. the amplitude of the harmonic \(2k+1\) decreases with \(8/\pi^2(2k + 1)^2\)

The amplitudes decreases quadratically with increasing frequencies.

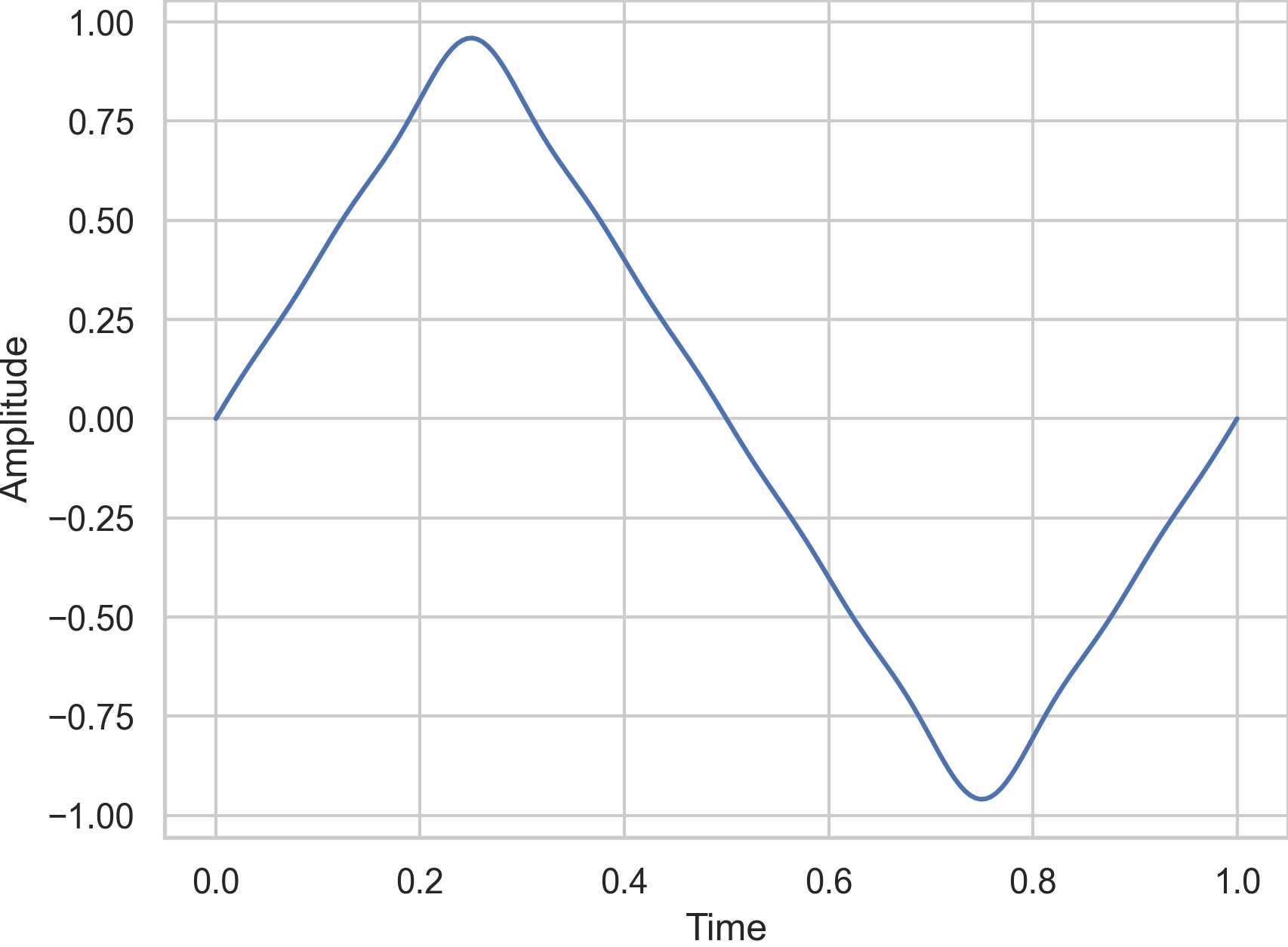
../../../_images/triangle_5.png

Fig. 44 An approximation for the Fourier series of the triangle wave with a frequency and amplitude of 1 using \(n=5\).#

The triangle wave is half way between the sine and the square wave, both in softness and in harmonic richness. It is pretty soft.

In sclang we can generate the sound of a triangle wave using the unit generator LFTri:

{LFTri.ar(220!2) * 0.25;}.play;

SuperCollider provides only the non-band-limited version of a triangle wave LFTri.

Summary#

Any periodic signal can be constructed from a sum of sine waves. The process of creating complex sounds from sine waves or other constituent parts is called additive synthesis. The sine wave, sawtooth wave, pulse wave, and triangle waves are classic waveforms since the advent of electronic music. They are used everywhere in the music we hear today and were/are the basis of many synthesizers. Sawtooth waves, pulse waves, and triangle waves come in bandlimited and non-bandlimited forms. Non-bandlimited forms can be produce strange artifacts at higher frequencies (see aliasing). Bandlimited forms are “safer” but are not as rich harmonically – they are not true representation of the waveforms.

From soft (and smooth), to rich (and aggressive), we can order the basic waveforms as follows:

  1. sine wave (SinOsc),

  2. triangle wave (LFTri),

  3. square wave (LFPulse, Pluse), and

  4. sawtooth wave (LFSaw, Saw)