Musical Event

Musical Event#

Pbind is an important Pattern. It models the process of playing an instrument by discrete events in time, realizing a discrete event simulation (DES). It streams (musical) Events.

Combining Streams

Pbind combines several value streams into one event stream.

We define a duration dur, the frequency freq, note note or midinote and the instrument we wanna play, i.e., the synth. A Pbind can then be played by calling play on it. The method returns an EventStreamPlayer.

Events extend Environments which manage namespaces. They are similar to hash maps, hash tables, or a Python dictionary, i.e., a collection where you can access elements by name. For example, calling a function will create a new local function environment. Environments map names to variables and functions.

(
var env = Environment.make({
    ~a = 100;
    ~b = 200;
    ~c = 300;
    ~add = {arg x, y; x + y;};
});
env.postln;
env[\a]; // 100
env[\add].(3,13); // 16
)

Here we define an environment with three variables a, b, c and a function add. ~a is in fact an abbreviation for currentEnvironment.at(\a) and ~a = 100 for currentEnvironment.put(\a, 100). As you can see we already worked with environments without knowing them.

We are not so much interested in environments but their subclass Event. Events can be defined using a far more compact syntax. We just use round brackets:

(
var event = (\dur: 1, \freq: 600); // define an event
event[\dur].postln; // 1
event.play; // play the event
)

What is going on here? We actually can hear a sound! Well, if you look at the post window, you can see all the predefined variables/symbols of the environment/event. In my case, this is equal to:

'instrument': default, 
'msgFunc': {}, 
'dur': 1, 
'amp': 0.1, 
'server': localhost, 
'sustain': 0.8, 
'isPlaying': true, 
'freq': 600.0, 
'hasGate': true, 
'id': [ 1869 ]

Everything we have to define to play a sound, such as, amp, instrument, server is predefined. The play method uses predefined values if they are missing in the event we want to play. The predefined values are stored in class variables, i.e., variables that are shared by all events. They are split into partial events:

Event.partialEvents.postln;

The Default Instrument#

The instrument is a default instrument called \default that is built into SuperCollider. We can find it in the source code of the Event class. Let us have a look:

SynthDef(\default, {
    arg out=0, freq=440, amp=0.1, pan=0, gate=1;
    var z;
    z = LPF.ar(
        Mix.new(
            VarSaw.ar(
                freq + [0, Rand(-0.4,0.0), Rand(0.0,0.4)], // freq
                0, // iphase
                0.3, // width
                0.3) // mul
        ),
        XLine.kr(Rand(4000,5000), Rand(2500,3200), 1) // cutoff
    ) * Linen.kr(gate, 0.01, 0.7, 0.3, 2); // * envelope
    OffsetOut.ar(out, Pan2.ar(z, pan, amp));
});

It is a filtered randomly distorted sawtooth wave with variable duty multiplied by a percussive envelope. Two slightly detuned waves are generated and mixed a single channel which is then panned into both speakers. The cutoff frequency of the low pass filter decreases over the time span of 1 second and is initialized with random values. By decreasing the cutoff frequency over time, high frequencies die out faster which is natural.

Value Conversions#

Playing events with Pbind (or Pbindef) using other patterns is a compelling but also inviting challenge. In my opinion, the main difficulty stems from the fact that each argument of the synth (and/or the play method) is defined by its own mostly independent stream of numbers. This invites you to think about each argument, such as frequency (\freq) and duration (\dur), independently, which is contrary to the western musical notation where a pair, namely pitch and duration, defines a musical note. Another source of confusion is the fact that Pbind allows you to specify the same class of arguments in different ways. For example, you can define the pitch (a specific class) via the frequency argument \freq a combination of \midinote, \harmonic, and other combinations of arguments. This flexibility is handy, but it can also feel overwhelming, especially for beginners.

Naming Convention of Synth Arguments

Note that one can only use specific arguments if the synth supports those. For example, we can neither use \freq nor \midinote if there is no argument freq used in the SynthDef of the synth we want to play!

In the Event class, we can also find the code that actually plays an event. The method of interest is called makeParentEvents. It is very lengthy, and you do not have to understand it. But if you are interested in what is precisely happening, it is a good starting point. Furthermore, it gives us information about all the default values. These values are also discussed in the official pattern guide. Another source of explanation can be found in the documentation of the Event class under section Useful keys for notes.

SuperCollider provides specification of different parameters that influence the scheduling and the execution of a single synth. But it provides different ways to express the same thing and converts it to a specific item. For example, a synth only knows frequencies, but you do not have to think in terms of frequencies. Instead, you can think in terms of midi notes, and the event player will transform your midi note into the respective frequency. Of course, defining midi note and simultaneously frequency does not really make sense. SuperCollider will always take the most substantial value, e.g., frequency over the midi note.

Timing#

First of all, time is measured in beats per second (bps), and events are scheduled on a specific TempoClock that runs at a particular bps. The default clock runs at 60 beats per second. We will discuss later how we can change this.

Let us look at the parameters determining the timing of a stream of events \(e_1, \ldots, e_n\). Let \(t_{i}\) be the start time of the event \(e_i\) (scheduled on our clock). Then \(t_{i+1} = t_{i} + \Delta t_{i}\) is the end time of \(e_{i}\) and the start time of the next scheduled event \(e_{i+1}\).

Furthermore, at \(t_{i} + \Delta_s t_{i}\) the sustain ends and the decay of the sound begins. \(\Delta t_{i}\) is equal to delta = dur * stretch and \(\Delta_s t_{i}\) is equal to sustain. The duration dur is stretched by a factor stretch. Of course, the sound of the event \(e_i\) can last longer than \(\Delta t_i\) especially if the sustain is longer than the final event duration delta:

\[\begin{equation*} \Delta_s t_{i} >\Delta t_i \end{equation*}\]

is feasible. We have the following parameters with their respective default values:

'tempo': nil,
'dur': 1.0,
'stretch': 1.0,
'legato': 0.8,
'sustain': { ~dur * ~legato * ~stretch },
'lag': 0.0,
'strum': 0.0,
'strumEndsTogether': false

Scheduling Influencer

dur, stretch, delta and lag influences the scheduling of events and may or may not influence the sound depending on the definition of other arguments.

First note that by default sustain is equal 0.8 * dur. In addition, we can either define sustain or legato but it does not really make sense to define them both because if sustain is defined, then the value of legato has no effect. This is not true for the duration dur, since it is not only used to compute sustain (if it is undefined).

Sound Influencer

legato and sustain do not influence the scheduling but the sound generated by the event!

What does lag mean? Well, lag \(\Delta t_l\) is a delay for the scheduler, i.e., scheduled events lag behind. The effect is that the sound generated by consecutive events will just start lag bps later.

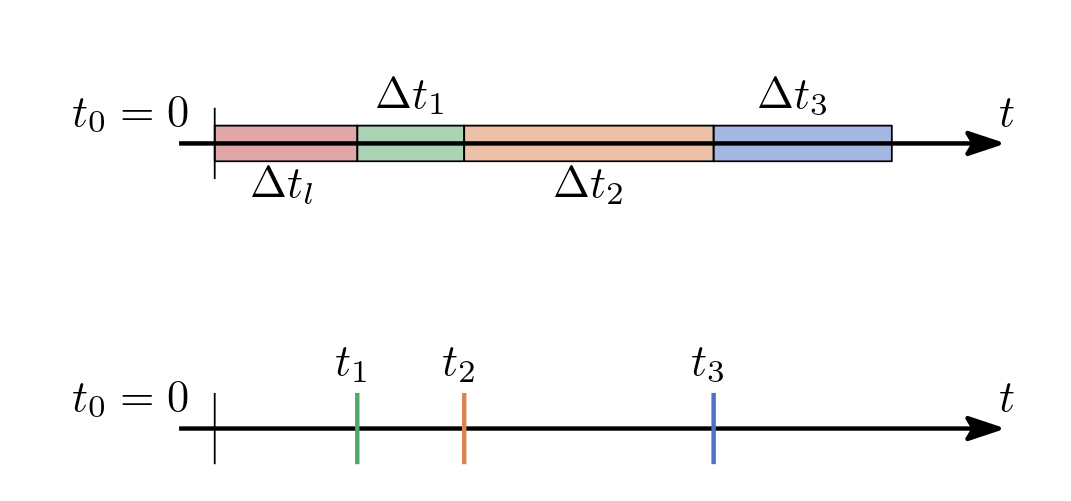
../../../_images/event-timing-dark.png — Fig. 9 Example of the timings of three scheduled events.#

Let \(e_1, \ldots, e_m\) be the \(m\) scheduled events. Then for all \(1 \leq i < m\)

\[\begin{equation*} t_{{i+1}} = t_{i} + \Delta t_{i} = t_0 + \Delta t_l + \Delta t_{1} + \ldots + \Delta t_{i} \end{equation*}\]

holds, where \(t_0\) is the time when the whole sequence got scheduled.

//2-second pause before the event is played
(\instrument: \default, \dur: 0.2, \freq: 300, \lag: 2).play;

One very specific argument one can use is \strum. It breaks a chord into multiple single notes which can be very handy. The default value is 0, i.e., no delay. In the following we play two chords two times but each note is delayed by 0.1 beats.

(
Pbind(
    \note, Pseq([[-7, 3, 7, 10], [0, 3, 5, 8]], 2),
    \dur, 1,
    \legato, 0.4,
    \strum, 0.1,
).play
)

Note that \strum does not influence \dur that is the next event will start at a time independent of the value of \strum. You can hear this if we increase the value to 0.5.

(
Pbind(
    \note, Pseq([[-7, 3, 7, 10], [0, 3, 5, 8]], 2),
    \dur, 1,
    \legato, 0.4,
    \strum, 0.5,
).play
)

In that case, you can hear that the notes 7, 0 and 10, 3 are played simultaniously since the next even starts after the notes -7 and 3 are played!

We will see the effect of the different timing parameters later on when we actually play a stream of events.

Pitch#

As already mentioned, we do not have to work with frequencies. In fact, there are many ways to define the pitch of the event, i.e., the played synth, and many of them are more relevant for musicians who are used to them.

One of the concepts are the so-called midi notes. It is baked into MIDI. This system assigns ascending numbers to the keys of a piano, defining C3 to be the midi note 60. The argument works together with \ctranspose and \harmonics. \ctranspose is added to \midinote. The overall formula looks like the following:

freq: #{
    (~midinote.value + ~ctranspose).midicps * ~harmonic;
}

We can add an additional detune to the frequency since the final detuned frequency that is sent to the synth is in fact detunedFreq:

detunedFreq: #{
    ~freq.value + ~detune
}

We could set detune to a high value, but to keep things clean, one should use the arguments as they are intended such that others and the future you and I can keep up with the code! Variable and argument names matter; they should mean something.

The function/message midicps transforms a midi note into its frequency, see section Utility Function.

(
(\instrument: \default, \dur: 0.2, \amp: 0.5, 
    \midinote: 60,
    \ctranspose: -6,
    \harmonic: 3
).play;
)

Is equivalent to

(
(\instrument: \default, \dur: 0.2, \amp: 0.5, 
    \freq: (60-6).midicps * 3).play;
)

We can also use the chromatic note index \note to compute the \midinote, which is handy if we do not want to work with midi notation but with a more musical-related notation that gives us a more flexible way to change certain properties of a note, e.g., the root and the specific octave we are playing it in. By default \note: 0 maps to \midinote: 60, i.e., C3. The following formula shows the exact relationship:

midinote: #{    // midinote is the midinote (continuous intermediate values)
    ((~note.value + ~gtranspose + ~root) / ~stepsPerOctave + ~octave) * 12.0;
}

If undefined ~stepsPerOctave is 12 (chromatic scale in Western music).

We can be even more abstract and use a specific scale instead of the chromatic one. In that case, we can specify the \degree within a scale. The combination of \degree, \root (tonic) and scale gives us a specific \note. In practice, we could define a Pbind using a certain key. Then we could play the whole pattern in another key by changing its scale.

note: #{
    (~degree + ~mtranspose).degreeToKey(~scale, ~stepsPerOctave);
}

stepsPerOctave defines how many note units map onto the octave. It supports non-12ET temperaments. I will not go into the details here. \mtranspose shifts/rotates the intervals of the scale combined with a shift of the root note. Therefore, we generate a different mode. For example, if you want to play in the key of A minor (Am) you can do so by choosing the minor scale and a \root of -3 or +9.

(
Pbind(
    \instrument, \default,
    \dur, 0.25, 
    \amp, 0.5,
    \scale, Scale.minor,        // minor
    \degree, Pseries(0, 1, 8),
    \root, -3                   // A
).play;
)

SuperColliders Scale is more like a mode, since we need the \root to define the actual scale. The default value of \root is 0, i.e., C.

If you are interested in more details, have a look at the source code of the Event class and its documentation. Furthermore, in chapter Music Theory, I give an overview of the basic principles of music theory with examples using SuperCollider.

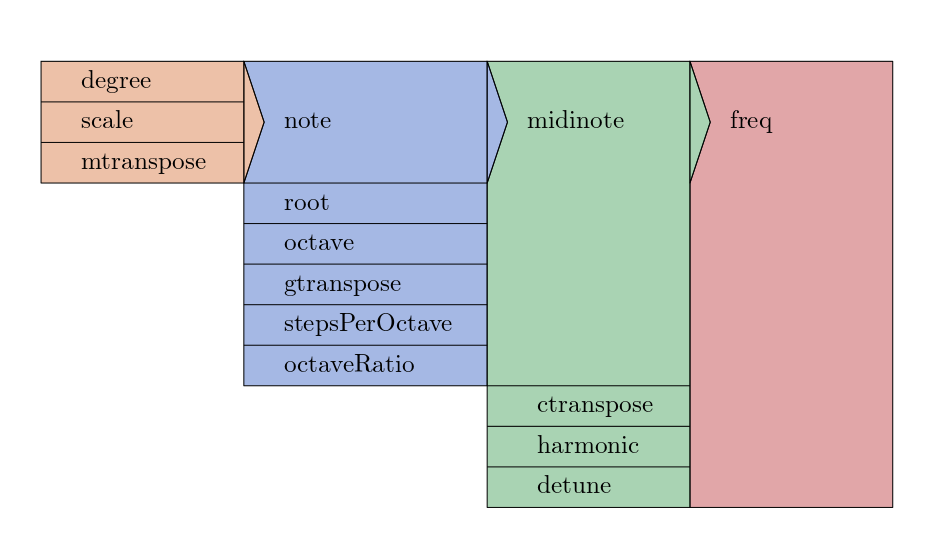
../../../_images/pitch-conversion-dark.png — Fig. 10 Overview of the pitch conversion. Source: SC documentation.#

Amplitude#

The amplitude can be defined by either \amp or \db (decibel). \amp has a higher prioritization and will override \db.

Both of the following code lines generate a sound of equal amplitude.

(\dur: 0.1, \freq: 600, \amp: -3.dbamp).play;
(\dur: 0.1, \freq: 600, \db: -3).play;

Amplitude in Decibel

\db: 0 equals \amp: 1.0.

Note that \db is a logarithmic unit used to measure sound level. Doubling the amplitude is approximately equal to adding 3 db.^

-6.dpamp    // 0.50118723362727
dbamp     // 1.0
dbamp     // 1.9952623149689
dbamp    // 3.981071705535

Custom Instrument#

Of course, we can use our own SynthDef, i.e., a custom instrument. To utilize all the excellent predefined parameters, our SynthDef has to use the correct arguments, and we have to name them as intended.

(
SynthDef(\snare,{arg hcutoff = 9000, lcutoff = 5000, amp = 1.4;
    var env, hat, bass, sig, cutoff = 5000;
    env = Env.perc(0.01, 0.15).kr(doneAction: Done.freeSelf);
    hat = {PinkNoise.ar()}!2;
    hat = HPF.ar(hat, XLine.ar(lcutoff/4, lcutoff, 0.2));
    hat = LPF.ar(hat, hcutoff);
    bass = LFTri.ar(XLine.kr(150, 10, 0.21))*0.2;
    sig = (hat + bass) * env * amp;
    Out.ar(0, sig);
}).add;
)

Synth(\snare)

(
SynthDef(\saw, {arg freq = 600, amp = 0.8, gate = 1, rel = 1.4;
    var sig, env, noise, cutoff;
    env = EnvGen.kr(
        Env.asr(attackTime: 0.01, sustainLevel: 0.5, releaseTime: rel), 
        gate: gate, 
        doneAction: Done.freeSelf);
	sig = LFSaw.ar([freq, freq*1.004]);
	cutoff = XLine.ar(freq*2, freq/4, 1.01+rel);
	sig = LPF.ar(sig, cutoff);
    sig = sig * env * amp;
    Out.ar(0, sig);
}).add;
)

~snare = Synth(\saw)
~snare.set(\gate, 0)

Note that the frequency argument should be called freq, the amplitude argument should be called amp, and the gate should be called gate. This is crucial. Otherwise, we can not make use of the full potential of SuperCollider’s pattern library.

(
var event = (\instrument: \saw, \dur: 0.2, \freq: 300);
event.play;
)

First, we add a very simple synth, then we play it for a duration of 0.2 beats per second (bps).

If we look closely, we can observe that there is a sustain argument that is set to 80 percent of the duration, i.e. to 0.16 beats per seconds. This is because the default values of our arguments are defined as follows.

'dur': 1.0,
'stretch': 1.0,
'legato': 0.8,
'sustain': { ~dur * ~legato * ~stretch },

As already mentioned, sustain is the time after the gate within our synth is triggered! We can change this default behavior by setting our own sustain value which overrides legato.

(
var event = (\instrument: \saw, \sustain: 0.1, \dur: 0.2, \freq: 300);
event.play;
)

Difference between Duration and Sustain

The duration dur is the elapsed time after the next event is scheduled while sustain is the time after the gate of the synth is triggered. If the sound sustains longer than dur we get overlapping sounds.

This seems to make the dur argument irrelevant. However, we need dur if we not only play one event but a Stream of events! Remember, dur influences the scheduler of our musical events. We can see the effect if we play a stream of events.

(
t = TempoClock(tempo: 1);

c = [0, 3, 4, 6, 0];

Pbind(
    \instrument, \saw,
    \scale, Scale.melodicMinor,
    \root, 1,
    \degree, Pseq(c, inf),
    \octave, 4,
    \rel, 0.1,
    \amp, 0.8,
    \dur, Pseq([0.25, 0.25, 0.25, 1.25], inf)
).play(t, quant: 1);

Pbind(
    \instrument, \saw,
    \scale, Scale.melodicMinor,
    \root, 1,
    \degree, Prand(c, inf),
    \octave, 7,
    \rel, 0.1,
    \amp, 0.3,
    \dur, 2
).play(t, quant: 1);

Pbind(
    \instrument, \snare,
    \dur, Pseq([0.25, 0.25, 0.5], inf),
    \amp, Pseq([1.5, 0.8, 0.8], inf),
    \hcutoff, Pseq([15000, 9000, 9000], inf)
).play(t, quant: 1)
)