Noise

If we define richness by the number of sine waves that are represented in a sound, then arguable the richest is pure noise. Interestingly this corresponds to the theory of information where a random message will eliminate the most amount of uncertainty thus has a high entropy.

In section Additive Synthesis we have noticed that the greater the number of enharmonic spectral elements there were, the more the sound approaches noise. In other words, if we add more and more sine waves, each with a random frequency, we will eventually and up with noise—the richest signal possible. Instead of adding more and more sine harmonics or inharmonics, subtractive synthesis starts by a rich signal, i.e., noise and filters specific frequencies.

Noise is often defined as all possible frequencies having equal representation. We can also define it as a wave with no pattern or maybe as a series of numbers of which we can not recognize its pattern. In a more general sense, noise is a random signal having intensity at a wide range of frequencies.

White Noise

White noise has equal intensity at different frequencies, giving it a constant power spectral density. Let us listen to white noise using the WhiteNoise unit generator.

{WhiteNoise.ar(0.25!2)}.play;

Note that we can not define the frequency since noise consist of a wide range of frequencies. White noise sounds similar to a FM radio while searching for a channel.

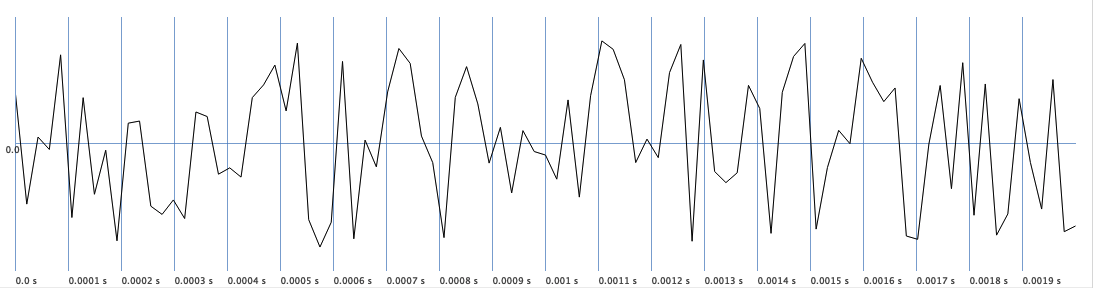
Fig. 47 A plot of WhiteNoise over a duration of 2 milliseconds.

If we look at the frequency analyser, we can see almost a line, i.e., all frequency have roughly equal power. Compared to other noises, the sound is rather harsh because of the power in high frequencies.

Pink Noise

To achieve a softer sound we can use the PinkNoise unit generator. Pink noise is exponentially biased towards lower frequencies. It has equal energy per octave band since musical octaves are exponential increasing with respect to frequency.

{PinkNoise.ar(0.25!2)}.play;

For pink noise the spectrum falls off in power by 3 dB per octave. It sounds more natural and full than white noise because it corresponds with the way we hear musical octaves. White noise appears brighter and thinner. Pink noise appears in nature at many places.

Brown Noise

The spectrum of brown noise realised by the BrownNoise unit generator falls even faster, that is, 6 dB in power per octave.

{BrownNoise.ar(0.25!2)}.play;

Clip Noise

The so called clip noise generated by the ClipNoise unit generator is even a little more harsh than WhiteNoise. It generates a high frequency stream of 1, -1 with equal probability.

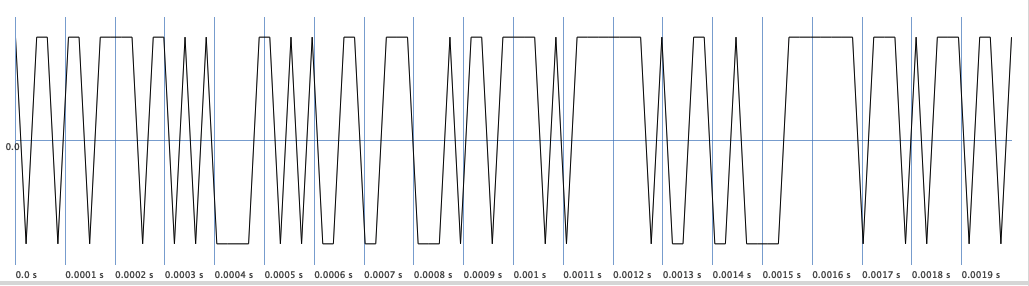
Fig. 48 A plot of ClipNoise over a duration of 2 milliseconds.

{ClipNoise.ar(0.25!2)}.play;

Gray Noise

The last available noise generator offered by the default sclang is GrayNoise which sounds very deep, like a heavy rain.

{GrayNoise.ar(0.25!2)}.play;

Reconstruction of Noises

We can create noise using additive synthesis. Let us use 1000 oscillators, that is, UGens. For pink noise we need an exponential distribution of frequencies while for white noise a linear distribution is required.

(
Ndef(\pink_noise, {
    var sig;
    sig = Mix.fill(1000, {SinOsc.ar(exprand(1.0, 20000))})*0.001;
    sig!2;
}).play;
)

(
Ndef(\white_noise, {
    var sig;
    sig = Mix.fill(1000, {SinOsc.ar(rrand(1.0, 20000))})*0.001;
    sig!2;
}).play;
)

On my machine, the CPU is at 20 percent. Using WhiteNoise or PinkNoise leads to almost no CPU workload.